常用排序算法、二
排序算法中的几个基本概念:
1.内部排序和外部排序
内部排序:将所有的排序记录都存储于计算机随机存储器中的排序过程;
外部排序:排序记录的数量过大,以致于不能将所有的排序记录一次性读入内存,因而在排序过程中还需对外存进行读取的过程。
2.稳定排序和不稳定排序
假设原排序序列:… R1, R2, …(排序键值KR1 = KR2)
稳定排序:排序之后,R1任然在R2的前面...R1,R2,...
不稳定排序:排序之后R1在R2后面...R2,R1,…
一,选择排序
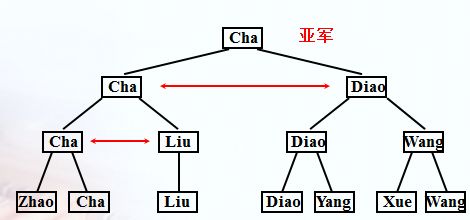
1.锦标赛排序
选择排序的主要操作时通过关键字比较从一堆排序序列中找到最值。比如,在直接选择排序中,从n个关键字中找出最值,需要n-1次比较,而在n-1个关键字中找出最值,需要n-2次比较…
事实上,在剩余的n-1个关键字中选出最小值,没必要在进行n-2次比较。前提是要利用前n-1次比较所获得的信息,这样就可以减少后面的比较次数。在下面这个8人的短跑比赛中,如果利用直接选择排序要比较7+6+5=18次,而用下面的树形排序可以将比较次数减至11场。
但是这个排序算法有一个缺点,由于树形结构中存在重复记录,所以这种排序方消耗大量空间。为了解决这个问题,可以改进算法,除去树形结构中的重复记录。
2.堆排序
堆的特性:一棵完全二叉树,任一个非终端结点的值均小于等于(或大于等于)其左、右儿子结点的值。
排序思路:首先,将所有排序记录,构造成一颗完全二叉树,然后再将这棵二叉树改成堆,此时在根节点可获最值;接着删除根节点,然后再把剩余树改成堆,获取剩余排序记录中的最值...依次进行删除根节点,改成堆的过程直到所有记录都被从树中删除的时候,就已经获得了一个排序。
二,归并排序
void merge(T A[], int Alen, T B[], int Blen, T C[]){
int i=0,j=0,k=0;
while(i < Alen && j < Blen){
if(A[i] < B[j])
C[k++] = A[i++];
else
C[k++] = B[j++];
}
while(i < Alen)
C[k++] = A[i++];
while(j < Blen)
C[k++] = B[j++];
}
void MergeSort(int A[], int B[], int l, int h)
{
if(l == h)
return;
int m = (l+h)/2;
MergeSort(A, B, l, m);
MergeSort(A, B, m+1, h);
Merge(A, B, l, m, h); //注意这里的归并是对一个序列的两段进行归并,需要对上面的算法进行修改,思想是一致的
}