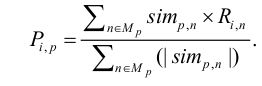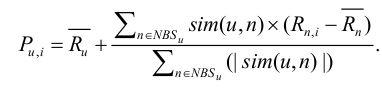协同过滤推荐算法
Collaborative Filtering Recommendation
转自：http://www.cnblogs.com/zhangchaoyang/articles/2664366.html
另，一定要看文献《协同过滤推荐算法综述》马宏伟
Pearson相关系数（相似性度量的方法）
度量向量之间的相似度方法很多了，你可以用距离（各种距离）的倒数，向量夹角，Pearson相关系数等。可参考《机器学习中的相似性度量》。
相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。
如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：
(1)、当相关系数为0时，X和Y两变量无关系。
(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。
相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度：
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
皮尔森相关系数计算公式如下：
分子是协方差，分母是两个变量标准差的乘积。显然要求X和Y的标准差都不能为0。
因为
,所以皮尔森相关系数计算公式还可以写成：
如果要自己计算, 可以参考 wiki 的这个公式:
x=[x1,x2......xn] y=[y1,y2......yn] 则上式可度量向量x与y之间的相似性。
当两个变量的线性关系增强时，相关系数趋于1或-1。
用户评分预测
基本原理：
step1.如果用户i对项目j没有评过分，就找到与用户i最相似的K个邻居（使用向量相似度度量方法）
step2.然后用这K个邻居对项目j的评分的加权平均来预测用户i对项目j的评分。
| |
iterm1 | ………… | itemn |
| user1 | R11 | |
R1n |
| …… | |
Rij | |
| userm | Rm1 | |
Rmn |
具体处理与改进：
step1.
用户评分矩阵是个高度稀疏的矩阵，即用户对很多项目都没有评分。在高度稀疏的情况下用传统的向量相似度度量方法来度量两个用户的相似度就会很不准确。一种简单的处理办法是对未评分的项都令其等于该用户的平均评分值。
度量用户 i 和用户 j 相似度更好的方法是：
1.用户 i 参与评分的项目集合为 Ii ，用户 j 参与评分的项目集合为 Ij ，找到它们的并集
2.在集合
中用户 i 未评分的项目是，用下面方法重新估计用户 i 对
中每个项目的评分：
2.1.取出评分矩阵的两列，计算这两列的相似度就是这两个项目的相似度。未被用户 i 评分的项目
，找到与
最相似的V个项目构成集合
。
2.2.
其中，表示项目p与项目n（项目n为与项目p最相似项目集合Mp中的项目）的相似度，
表示用户 i 对项目n的评价值。
3.这样用户 i 和 j 对的评分就都是非0值了，在此情况下计算他们的相似度。
step2.
利用与用户u相似的用户n来预测用户u对项目i的评价：
表示用户u对所有评分过的项目的评分平均值,用户n为用户u的相似用户，为相似用户n对项目i的评价，
为所有相似用户对项目i评价的平均值，sim(u,n)为用户u与其相似用户n的相似度。
完了，可以看到算法非常的简单，核心就是计算向量的相似度。代码量也很少。
#include<iostream> #include<queue> #include<cmath> #include<cassert> #include<cstdlib> #include<fstream> #include<sstream> #include<vector> #include<algorithm> using namespace std; const int ITERM_SIZE=1682; const int USER_SIZE=943; const int V=15; //ITERM的最近邻居数 const int S=10; //USER的最近邻居数 struct MyPair{ int id; double value; MyPair(int i=0,double v=0):id(i),value(v){} }; struct cmp{ bool operator() (const MyPair & obj1,const MyPair & obj2)const{ return obj1.value < obj2.value; } }; double rate[USER_SIZE][ITERM_SIZE]; //评分矩阵 MyPair nbi[ITERM_SIZE][V]; //存放每个ITERM的最近邻居 MyPair nbu[USER_SIZE][S]; //存放每个USER的最近邻居 double rate_avg[USER_SIZE]; //每个用户的平均评分 //从文件中读入评分矩阵 int readRate(string filename){ ifstream ifs; ifs.open(filename.c_str()); if(!ifs){ cerr<<"error:unable to open input file "<<filename<<endl; return -1; } string line; while(getline(ifs,line)){ string str1,str2,str3; istringstream strstm(line); strstm>>str1>>str2>>str3; int userid=atoi(str1.c_str()); int itermid=atoi(str2.c_str()); double rating=atof(str3.c_str()); rate[userid-1][itermid-1]=rating; line.clear(); } ifs.close(); return 0; } //计算每个用户的平均评分 void getAvgRate(){ for(int i=0;i<USER_SIZE;++i){ double sum=0; for(int j=0;j<ITERM_SIZE;++j) sum+=rate[i][j]; rate_avg[i]=sum/ITERM_SIZE; } } //计算两个向量的皮尔森相关系数 double getSim(const vector<double> &vec1,const vector<double> &vec2){ int len=vec1.size(); assert(len==vec2.size()); double sum1=0; double sum2=0; double sum1_1=0; double sum2_2=0; double sum=0; for(int i=0;i<len;i++){ sum+=vec1[i]*vec2[i]; sum1+=vec1[i]; sum2+=vec2[i]; sum1_1+=vec1[i]*vec1[i]; sum2_2+=vec2[i]*vec2[i]; } double ex=sum1/len; double ey=sum2/len; double ex2=sum1_1/len; double ey2=sum2_2/len; double exy=sum/len; double sdx=sqrt(ex2-ex*ex); double sdy=sqrt(ey2-ey*ey); assert(sdx!=0 && sdy!=0); double sim=(exy-ex*ey)/(sdx*sdy); return sim; } //计算每个ITERM的最近邻 void getNBI(){ for(int i=0;i<ITERM_SIZE;++i){ vector<double> vec1; priority_queue<MyPair,vector<MyPair>,cmp> neighbour; for(int k=0;k<USER_SIZE;k++) vec1.push_back(rate[k][i]); for(int j=0;j<ITERM_SIZE;j++){ if(i==j) continue; vector<double> vec2; for(int k=0;k<USER_SIZE;k++) vec2.push_back(rate[k][j]); double sim=getSim(vec1,vec2); MyPair p(j,sim); neighbour.push(p); } for(int j=0;j<V;++j){ nbi[i][j]=neighbour.top(); neighbour.pop(); } } } //预测用户对未评分项目的评分值 double getPredict(const vector<double> &user,int index){ double sum1=0; double sum2=0; for(int i=0;i<V;++i){ int neib_index=nbi[index][i].id; double neib_sim=nbi[index][i].value; sum1+=neib_sim*user[neib_index]; sum2+=fabs(neib_sim); } return sum1/sum2; } //计算两个用户的相似度 double getUserSim(const vector<double> &user1,const vector<double> &user2){ vector<double> vec1; vector<double> vec2; int len=user1.size(); assert(len==user2.size()); for(int i=0;i<len;++i){ if(user1[i]!=0 || user2[i]!=0){ if(user1[i]!=0) vec1.push_back(user1[i]); else vec1.push_back(getPredict(user1,i)); if(user2[i]!=0) vec2.push_back(user2[i]); else vec2.push_back(getPredict(user2,i)); } } return getSim(vec1,vec2); } //计算每个USER的最近邻 void getNBU(){ for(int i=0;i<USER_SIZE;++i){ vector<double> user1; priority_queue<MyPair,vector<MyPair>,cmp> neighbour; for(int k=0;k<ITERM_SIZE;++k) user1.push_back(rate[i][k]); for(int j=0;j<USER_SIZE;++j){ if(j==i) continue; vector<double> user2; for(int k=0;k<ITERM_SIZE;++k) user2.push_back(rate[j][k]); double sim=getUserSim(user1,user2); MyPair p(j,sim); neighbour.push(p); } for(int j=0;j<S;++j){ nbu[i][j]=neighbour.top(); neighbour.pop(); } } } //产生推荐，预测某用户对某项目的评分 double predictRate(int user,int iterm){ double sum1=0; double sum2=0; for(int i=0;i<S;++i){ int neib_index=nbu[user][i].id; double neib_sim=nbu[user][i].value; sum1+=neib_sim*(rate[neib_index][iterm]-rate_avg[neib_index]); sum2+=fabs(neib_sim); } return rate_avg[user]+sum1/sum2; } //测试 int main(){ string file="/home/orisun/DataSet/movie-lens-100k/u.data"; if(readRate(file)!=0){ return -1; } getAvgRate(); getNBI(); getNBU(); while(1){ cout<<"please input user index and iterm index which you want predict"<<endl; int user,iterm; cin>>user>>iterm; cout<<predictRate(user,iterm)<<endl; } return 0; }