学习Opencv2.4.9(四)---SVM支持向量机

• 先来看一下什么是SVM(支持向量机)

SVM是一种训练机器学习的算法，可以用于解决分类和回归问题，同时还使用了一种称之为kernel trick（支持向量机的核函数）的技术进行数据的转换，然后再根据这些转换信息，在可能的输出之中找到一个最优的边界(超平面)。简单来说，就是做一些非常复杂的数据转换工作，然后根据预定义的标签或者输出进而计算出如何分离用户的数据。

支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力（或称泛化能力）。

• 支持向量机较其他传统机器学习算法的优点：

1、小样本，并不是说样本的绝对数量少（实际上，对任何算法来说，更多的样本几乎总是能带来更好的效果），而是说与问题的复杂度比起来，SVM算法要求的样本数是相对比较少的。SVM解决问题的时候，和样本的维数是无关的（甚至样本是上万维的都可以，这使得SVM很适合用来解决文本分类的问题，当然，有这样的能力也因为引入了核函数）。

2、结构风险最小。（对问题真实模型的逼近与问题真实解之间的误差，就叫做风险，更严格的说，误差的累积叫做风险）。

3、非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也有人叫惩罚变量）和核函数技术来实现，这一部分是SVM的精髓。（关于文本分类这个问题究竟是不是线性可分的，尚没有定论，因此不能简单的认为它是线性可分的而作简化处理，在水落石出之前，只好先当它是线性不可分的反正线性可分也不过是线性不可分的一种特例而已，我们向来不怕方法过于通用）。

• SVM的强大离不开一个很重要的东西--核函数：

1、为何需要核函数？

很多情况下低维空间向量集是难于划分的，解决办法是将它们映射到高维空间。但这个办法带来的艰苦就是策画错杂度的增长，而核函数正好奇妙地解决了这个问题。也就是说，只要选用恰当的核函数，就可以获得高维空间的分类函数（超平面）。在SVM理论中，采取不合的核函数将导致不合的SVM算法。在断定了核函数之后，因为断定核函数的已知数据也存在必然的误差，推敲到推广性题目，是以引入了败坏系数以及处罚系数两个参变量来加以校订。

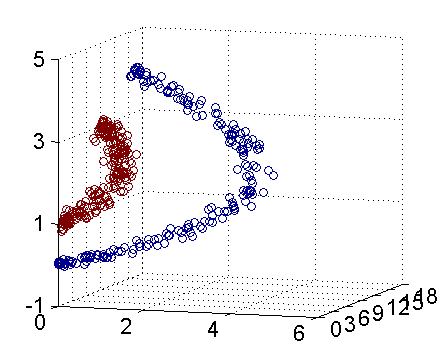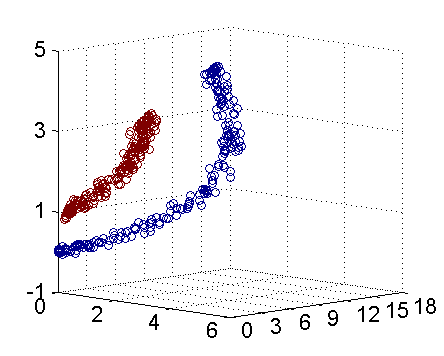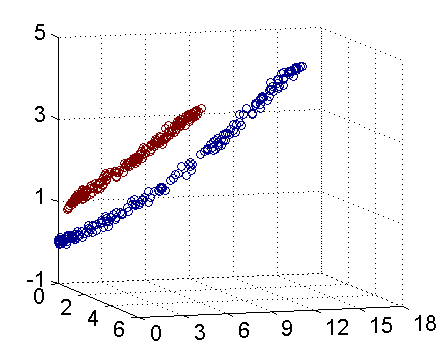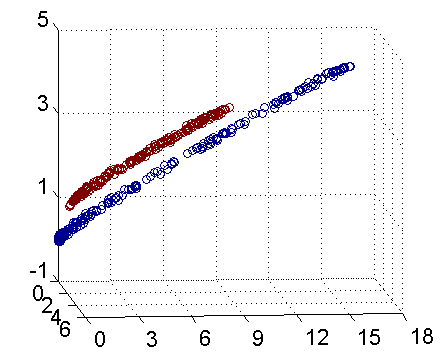
其实核函数的本质作用可以简练概括为：将低维空间的线性不可分类问题，借助核函数转化为高维空间的线性可分，进而可以在高维空间找到分类的最优边界（超平面）。(下图引自July‘s 支持向量机通俗导论（理解SVM的三层境界）)。若要要分类下图红色和蓝色样本点：

              

                           二维线性不可分                                                                                                                三维线性可分

2、核函数的分类

(1)线性核函数

(2)多项式核函数

(3)径向基（RBF）核函数（高斯核函数）

(4)Sigmoid核函数（二层神经收集核函数）

3、Opencv中的核函数定义：

CvSVM::LINEAR : 线性内核，没有任何向映射至高维空间，线性区分（或回归）在原始特点空间中被完成，这是最快的选择。

.

CvSVM::POLY : 多项式内核：

.

CvSVM::RBF : 基于径向的函数，对于大多半景象都是一个较好的选择：

.

CvSVM::SIGMOID : Sigmoid函数内核：

.

• Opencv中SVM参数设置：

Opencv中SVM参数设置使用CvSVMParams方法定义如下：

 CvSVMParams::CvSVMParams（int svm_type，
 int kernel_type，
 double degree，
 double gamma，
 double coef0，
 double Cvalue，
 double nu，
 double p，
 CvMat* class_weights，
 CvTermCriteria term_crit
 ）

CvSVMParams方法如果不传自定义参数会按如下代码进行默认初始化：

 CvSVMParams::CvSVMParams（） : svm_type（CvSVM::C_SVC）， kernel_type（CvSVM::RBF）， degree（0），
     gamma（1）， coef0（0）， C（1）， nu（0）， p（0）， class_weights（0）
 {
     term_crit = cvTermCriteria（ CV_TERMCRIT_ITER+CV_TERMCRIT_EPS， 1000， FLT_EPSILON ）;
 }

kernel_type:SVM的内核类型（4种）：

上面已经介绍过了就不再多说了。

svm_type:指定SVM的类型（5种）：

1、CvSVM::C_SVC : C类支撑向量分类机。 n类分组 （n≥2），容许用异常值处罚因子C进行不完全分类。

2、CvSVM::NU_SVC : 类支撑向量分类机。n类似然不完全分类的分类器。参数为庖代C（其值在区间【0，1】中，nu越大，决定计划鸿沟越腻滑）。

3、CvSVM::ONE_CLASS : 单分类器，所有的练习数据提取自同一个类里，然后SVM建树了一个分界线以分别该类在特点空间中所占区域和其它类在特点空间中所占区域。

4、CvSVM::EPS_SVR : 类支撑向量回归机。练习集中的特点向量和拟合出来的超平面的间隔须要小于p。异常值处罚因子C被采取。

5、CvSVM::NU_SVR : 类支撑向量回归机。 庖代了 p。

degree:内核函数（POLY）的参数degree。

gamma:内核函数（POLY/ RBF/ SIGMOID）的参数。

coef0:内核函数（POLY/ SIGMOID）的参数coef0。

Cvalue:SVM类型（C_SVC/ EPS_SVR/ NU_SVR）的参数C。

nu:SVM类型（NU_SVC/ ONE_CLASS/ NU_SVR）的参数 。

p:SVM类型（EPS_SVR）的参数。

class_weights:C_SVC中的可选权重，赋给指定的类，乘以C今后变成 。所以这些权重影响不合类此外错误分类处罚项。权重越大，某一类此外误分类数据的处罚项就越大。

term_crit:SVM的迭代练习过程的中断前提，解决项目组受束缚二次最优题目。您可以指定的公差和/或最大迭代次数。

• Opencv中SVM训练函数：

 CvSVM::train（const CvMat* trainData，
 const CvMat* responses，
 const CvMat* varIdx=0，
 const CvMat* sampleIdx=0，
 CvSVMParams params=CvSVMParams（）
 ）

1、trainData: 练习数据，必须是CV_32FC1 （32位浮点类型，单通道）。数据必须是CV_ROW_SAMPLE的，即特点向量以行来存储。

2、responses: 响应数据，凡是是1D向量存储在CV_32SC1 （仅仅用在分类题目上）或者CV_32FC1格局。

3、varIdx: 指定感爱好的特点。可所以整数（32sC1）向量，例如以0为开端的索引，或者8位（8uC1）的应用的特点或者样本的掩码。用户也可以传入NULL指针，用来默示练习中应用所有变量／样本。

4、sampleIdx: 指定感爱好的样本。描述同上。

5、params: SVM参数。

• Opencv中的SVM识别（预言）函数：

Opencv的预言函数所有重载如下：

 float CvSVM::predict（const Mat& sample， bool returnDFVal=false ） const
 float CvSVM::predict（const CvMat* sample， bool returnDFVal=false ） const
 float CvSVM::predict（const CvMat* samples， CvMat* results） const

    1、sample:  须要猜测的输入样本。

2、samples: 须要猜测的输入样本们。

3、returnDFVal: 指定返回值类型。若是值是true，则是一个2类分类题目，该办法返回的决定计划函数值是边沿的符号间隔。

4、results: 响应的样本输出猜测的响应。

这个函数用来猜测一个新样本的响应数据（response）。

在分类题目中，这个函数返回类别编号；在回归题目中，返回函数值。

输入的样本必须与传给trainData的练习样本同样大小。

若是练习中应用了varIdx参数，必然记住在predict函数中应用跟练习特点一致的特点。

• Opencv中SVM分类问题代码流程：

（1）获得练习样本及制作其类别标签（trainingDataMat，labelsMat）

（2）设置练习参数（CvSVMParams）

（3）对SVM进行训练（CvSVM::train）

（4）对新的输入样本进行猜测（CvSVM::predict），并输出结果类型（对应标签）

（5）获取支撑向量（CvSVM::get_support_vector_count，CvSVM::get_support_vector ）

• SVM多类分类问题的几种方法：

目前，构造SVM多类分类器的方法主要有两类：一类是直接法，直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类。这种方法看似简单，但其计算复杂度比较高，实现起来比较困难，只适合用于小型问题中；另一类是间接法，主要是通过组合多个二分类器来实现多分类器的构造，常见的方法有one-against-one和one-against-all两种。

1、一对多法（one-versus-rest,简称OVRSVMs）。训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。

假如我有四类要划分（也就是4个Label），他们是A、B、C、D。于是我在抽取训练集的时候，分别抽取A所对应的向量作为正集，B,C,D所对应的向量作为负集；B所对应的向量作为正集，A,C，D所对应的向量作为负集；C所对应的向量作为正集，A,B,D所对应的向量作为负集；D所对应的向量作为正集，A,B,C所对应的向量作为负集，这四个训练集分别进行训练，然后的得到四个训练结果文件，在测试的时候，把对应的测试向量分别利用这四个训练结果文件进行测试，最后每个测试都有一个结果f1(x),f2(x),f3(x),f4(x).于是最终的结果便是这四个值中最大的一个。

PS:这种方法有种缺陷,因为训练集是1:M,这种情况下存在偏差.因而不是很实用.

2、一对一法（one-versus-one,简称OVOSVMs或者pairwise）。其做法是在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。

还是假设有四类A,B,C,D四类。在训练的时候我选择A,B;A,C; A,D; B,C;B,D;C,D所对应的向量作为训练集，然后得到六个训练结果，在测试的时候，把对应的向量分别对六个结果进行测试，然后采取投票形式，最后得到一组结果。

3、层次支持向量机（H-SVMs）。层次分类法首先将所有类别分成两个子类，再将子类进一步划分成两个次级子类，如此循环，直到得到一个单独的类别为止。

4、DAG-SVMS是由Platt提出的决策导向的循环图DDAG导出的,是针对“一对一”SVMS存在误分、拒分现象提出的。

这里仅仅是对几种多分类方法的简要说明，如果直接调用Opencv的predict方法，并不需要关心多分类算法的具体实现，来看看下面的例子：

• Opencv中SVM多类分类问题编程实例：

 #include <cv.h>
 #include <highgui.h>
 #include <ml.h>
 #include <cxcore.h>

 #include <iostream>
 using namespace std;

 int main()
 {
  // step 1:
 //训练数据的分类标记，即4类
  float labels[16] = {1.0, 1.0,1.0,1.0,2.0,2.0,2.0,2.0,3.0,3.0,3.0,3.0,4.0,4.0,4.0,4.0};
  CvMat labelsMat = cvMat(16, 1, CV_32FC1, labels);
  //训练数据矩阵
  float trainingData[16][2] = { {0, 0}, {4, 1}, {4, 5}, {-1, 6},{3,11},{-2,10},{4,30},{0,25},{10,13},{15,12},{25,40},{11,35},{8,1},{9,6},{15,5},{20,-1} };
  CvMat trainingDataMat = cvMat(16, 2, CV_32FC1, trainingData);

  // step 2:
  //训练参数设定
  CvSVMParams params;
  params.svm_type = CvSVM::C_SVC;                 //SVM类型
  params.kernel_type = CvSVM::LINEAR;             //核函数的类型

  //SVM训练过程的终止条件, max_iter:最大迭代次数  epsilon:结果的精确性
  params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, FLT_EPSILON );

  // step 3:
  //启动训练过程
  CvSVM SVM;
  SVM.train( &trainingDataMat, &labelsMat, NULL,NULL, params);

  // step 4:
  //使用训练所得模型对新样本进行分类测试
  for (int i=-5; i<15; i++)
  {
       for (int j=-5; j<15; j++)
       {
            float a[] = {i,j};
            CvMat sampleMat;
            cvInitMatHeader(&sampleMat,1,2,CV_32FC1,a);
            cvmSet(&sampleMat,0,0,i);                                        // Set M(i,j)
            cvmSet(&sampleMat,0,1,j);                                        // Set M(i,j)
            float response = SVM.predict(&sampleMat);
            cout<<response<<" ";
       }
       cout<<endl;
  }

  // step 5:
  //获取支持向量
  int c = SVM.get_support_vector_count();
  cout<<endl;
  for (int i=0; i<c; i++)
  {
       const float* v = SVM.get_support_vector(i);
       cout<<*v<<" ";
  }
  cout<<endl;

  system("pause");
  return 0;
 }

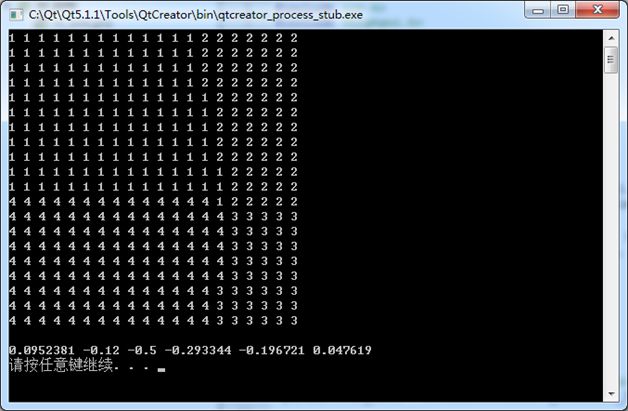
运行结果：

PS： 统计学习泛化误差界的概念，就是指真实风险应该由两部分内容刻画，一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然，第二部分是没有办法精确计算的，因此只能给出一个估计的区间，也使得整个误差只能计算上界，而无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。

置信风险与两个量有关，一是样本数量，显然给定的样本数量越大，我们的学习结果越有可能正确，此时置信风险越小；二是分类函数的VC维，显然VC维越大，推广能力越差，置信风险会变大。 
泛化误差界的公式为：R(w)≤Remp(w)+Ф(n/h) 
公式中R(w)就是真实风险，Remp(w)就是经验风险，Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构风险最小。 
SVM正是这样一种努力最小化结构风险的算法。