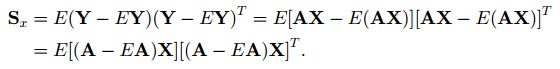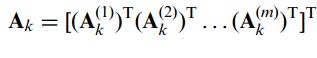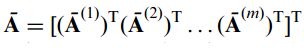2DPCA以及增强的双向2DPCA详解

　　最近在做目标追踪的过程中用到了2DPCA变换，花了两天时间研究了下2DPCA的起源及其重要改进，在此稍作总结。

     相关原始文献

　　1、一维PCA及其不足之处

　　在介绍2DPCA之前，稍微提一下历史悠久的PCA变换，一句话总结PCA变换：“通过求解目标协方差矩阵的前N个最大特征值对应的特征向量来组成特征映射矩阵以实现样本的主成分空间映射。”，可能有点笼统，其余的传统PCA的知识大家可以自行百度吧。

　　我们这里主要探讨在图像处理过程中的PCA变换。由于图像本身为一个二维矩阵（以灰度图为例），传统PCA在构造协方差矩阵时需要先将图像转换成行向量的形式，然后将多个样本图片对应的多个行向量组成一个大规模的协方差矩阵，然后求解此协方差矩阵的特征值及特征向量来构建映射矩阵。这里就存在两个问题：（1）每次进行PCA变换前都需要将二维矩阵（图片）转换为一维矩阵（行向量），也就避免不了对图片进行遍历，在图片数量很多、尺寸较大的情况下，这一步是很耗时的。（2）得到的协方差矩阵的尺寸通常情况下也很大。举个例子，有100张样本，每个样本的尺寸均为100*100，那么对应每个行向量为1*10000，则最终的协方差矩阵为100*10000，对于这样大规模的矩阵进行SVD分解，效率可想而知，此时，2DPCA应运而生。

　　2、2DPCA的起源以及推导

　　首先在这里给出2DPCA的原始文献：《Two-Dimensional PCA:A New Approach to Appearance-Based Face Representation and Recognition》大家可以在EI检索、IEEE检索、谷歌学术、百度文库中下载到这篇文献（我稍后也会上传到CSDN网站），如果大家不介意阅读英文文献的话，建议好好研读一下这篇2004年发表的论文。

　　接下里言归正传，对于原始的图片A，尺寸为m*n，需要将其通过映射矩阵X投影到另外一个子空间（主成分空间），即：

　　这里Y为投影结果，简单说一下各个变量的尺寸：A为m*n矩阵，X为n*1的列向量，Y为m*1的特征向量。这里我们需要找到最佳的投影矩阵X以保证映射结果能够保留最大程度的信息。理想的投影矩阵应该保证投影后的结果尽量分开，即散度达到最大，因此我们用如下标准作为衡量投影矩阵X性能的目标函数：

　　这里的Sx代表的是投影结果（Y）的协方差矩阵，tr（Sx）代表协方差矩阵的迹，用以反映的投影后的样本间的散度，Y的协方差矩阵Sx的定义及简单推导如下：

　　然后根据tr（AB）= tr（BA），可得：

　　这是我们发现中间那部分正好代表数据矩阵A的协方差矩阵，因此我们将其单独定义为Gt，Gt即代表数据矩阵A的协方差矩阵：

　　这里Gt应该是一个n*n的方阵。对于M张训练样本A（j）（j = 1，2，……，M），可得其协方差矩阵为：

　　此时，可将之前投影矩阵X的目标函数简化为：

　　接下来，就是2DPCA的精华部分了，为了证明权威性，我们先提供作者在论文中的原话：

　　文章说的很清楚，投影矩阵X的最优解即是协方差矩阵Gt的前n个最大的特征值对应的特征向量组成的矩阵，这又回到了原始的PCA定义了，正所谓万变不离其宗，既然归根到底都是PCA，最终的核心部分还是相同的。因此所谓的2DPCA，就是先通过样本集得到样本集的协方差矩阵，只不过此时的协方差矩阵不是按照之前的那种先变成行向量然后再堆叠出来，而是直接将所有样本累加再求平均得到的，然后对得到的协方差矩阵进行特征值分解，将对应的特征向量排列起来即得到了最优的投影矩阵。

　　简单分析一下2DPCA的优点。首先很明显的一点是其不需要再将图像向量化，节约不少时间；其次就是需要做特征值分解的协方差矩阵现对于传统的PCA尺寸要小很多，同样100张100*100的图片，一维PCA所用到的协方差矩阵尺寸为100*10000，2DPCA的协方差矩阵仍为100*100，差别显而易见。作者在论文中证明了2DPCA在人脸识别等方面性能是优于一维PCA的。

　　3、改进的双向2DPCA

　　在2DPCA提出的第二年，即有学者对其进行了重大改进，这里暂且称其为双向2DPCA。

　　首先给出双向2DPCA的原始文献：《（2D）2PCA: Two-directional two-dimensional PCA for efficient face representation and recognition》，同样可以通过EI检索、IEEE检索、百度学术、谷歌学术来获取这篇文献，这篇文献是在2005年发表的，可以说，今天人们所谈到的2DPCA，几乎都是指经过这篇论文改进的双向2DPCA了。这里所指的双向，是指在行方向和列方向都进行一次2DPCA运算。

　　当然无论是哪种2DPCA，训练样本集（M张）的协方差矩阵都是必不可少的：

　　为了详细起见，这里给出训练样本集均值模板的表示形式：

　　这里我们不妨将矩阵A表示行向量组的形式：

　　以及：

　　这里Ak（1）等等都代表了元矩阵A的一行元素，矩阵共有m行，则此时训练集的协方差矩阵可以进一步表示为：

  

　　那么重点来了，仔细观察这个协方差矩阵的表示形式就会发现，其实它和之前最原始的2DPCA的协方差矩阵Gt的表示形式本质上是一样的，只不过多了行方向上的叠加而已，因此我们成之前的2DPCA是工作在行方向上的PCA变换。接下来只需要按照之前介绍的方式对协方差矩阵G进行特征值分解等一系列操作，即可得到相应的映射矩阵，不过这里得到的是行映射矩阵X（又称左映射矩阵）。

　　以此类推，接下来就应该介绍工作在列方向上的2DPCA了，原理和上面的类似，只不过上面公式总矩阵A采用的是按行排列，接下来我们将其改为按列排列：

　　以及：

　　注意这里既然是按列排列，则省去了不少的转置操作，相应的，此时的训练集协方差矩阵应该调整为如下形式：

　　这里协方差矩阵的尺寸应为m*m，细心的读者应该已经猜到了，接下来我们就是对G进行特征值分解，从而能得到一个新的特征映射矩阵，这个映射矩阵时工作在列方向上的，我们暂时将其命名为Z，即列映射矩阵（右映射矩阵），尺寸为m*d。

　　接下里我们将行映射矩阵和列映射矩阵进行简单归纳，对于行映射矩阵，其映射形式为：

　　目标函数为：

　　协方差矩阵为：

　　对于列映射矩阵，其映射形式为：

　　这里B为映射结果，Z为投影矩阵。对应目标函数为：

　　协方差矩阵为：

　　细心观察发现，行映射的协方差矩阵和列映射的协方差矩阵区别就在于转置相乘的顺序上。

　　3、重构

　　得到行、列方向上的投影矩阵X、Z之后，其联合映射的形式如下：

　　对于原矩阵的重构结果如下：

　　这里的Z和X都是正交矩阵，与转置相乘结果为一，因此有了这种重构表达式，至此，改进的双向2DPCA推导完成。

　　4、一点想法

　　双向2DPCA与原始的2DPCA先比最大的优势在于其映射结果C的维数很小，为d*d（d为选取的主成分的数量），一定程度上算是完成了对2DPCA的降维操作。直观上说，要计算双向2DPCA的左右投影矩阵只需进行两次协方差的特征值分解即可，但人们跟倾向于将其与稀疏优化问题放在一起求解。在最近很多2DPCA的应用中，在求解映射矩阵稀疏时都运用了凸优化理论，有兴趣的可以深入研究一下。