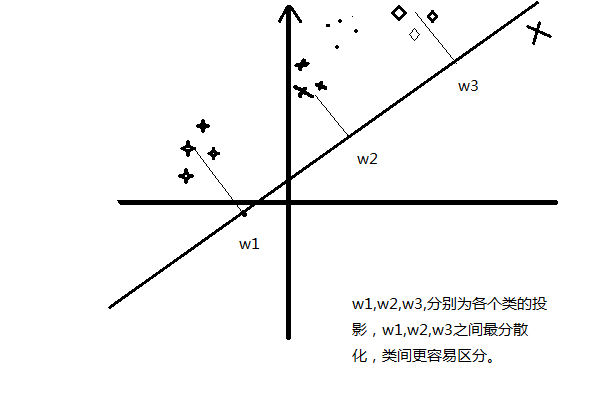
2D-PCA

传统的一维PCA和LDA方法是在图像识别的时候基于图像向量，在这些人脸识别技术中，2D的人脸图像矩阵必须先转化为1D的图像向量，然后进行PCA或者LDA分析。缺点是相当明显的：

 　　一、转化为一维之后，维数过大，计算量变大。

　　二、主成分分析的训练是非监督的，即PCA无法利用训练样本的类别信息。

　　三、识别率不是很高。

本文介绍的是2DPCA，2DPCA顾名思义是利用图像的二维信息。

      2DPCA算法简介

　　设X表示n维列向量，将mxn的图像矩阵A通过如下的线性变化直接投影到X上：

　　　　　　　　　　

得到一个m维的列向量Y,X为投影轴，Y称为图像A的投影向量。最佳投影轴X可以根据特征相怜Y的散度分布情况来决定，采用的准则如下：

　　　　　　　　　　　　

其中Sx表示的是训练样本投影特征向量Y的协方差矩阵，tr(Sx)带便的是Sx的迹，但此准则去的最大的值得时候，物理意义是：找到一个将所有训练样本投影在上面的投影轴X，使得投影后的所得到的的特征向量的总体散布矩阵（样本类之间的散布矩阵）最大化。矩阵Sx可以记为如下的式子：

　所以呀，

                         　　　　

散度的形象化理解：

　　　　　　　　　　　　　　　　　

我们接着定义下面的矩阵：

                             　　

其中Gt被定义为图像的协方差矩阵，它是一个nxn的矩阵，我们可以后直接利用训练样本来计算Gt。假设训练样本总数为M个，训练图像样本为mxn的矩阵Aj(j=1...M),所有的训练样本的平均图像是，则Gt可以用下面的式子计算：

　　　　　　　　　　　　　　　　

那么原式可以转化为

其中X是归一化的正交向量。这个准则就叫做广义总体散布准则。二X就使准则最大化，叫做最佳投影轴。物理意义是：图像矩阵在轴上面投影之后得到的特征向量的总体分散程度最大。

 这里的最佳投影轴Xopt是归一化的向量，使得J(X)最大化。

我们通常选取一系列的标准正交话投影轴，即设Gt的特征值从大到小，则对应的向量为：

　　

图像的特征矩阵：

      X1，...Xd可以用于特征的提取。对于一个给定的图像样本A,有下面的式子成立：

 

这样我们就得到一组投影特征向量Y1，...Yd,叫图像A的主要成分向量。2DPCA选取一定数量d的主要成分向量可以组成一个mxd的矩阵，叫图像A的特征或者特征图像，即：

　　

利用上面得到的特征图像进行分类：

         经过上面的图像特征化之后，每个图像都能得到一个特征矩阵。设有C个已知的模式分类w1,w2,.....wc，ni表示第i类的训练样本数，训练样本图像的投影特征向量,（i=1,2...C;j=1,2...,ni）,第i类投影特征向量的均值为，在投影空间内部，最邻近分类规则是：如果样本Y满足：

同时最小距离分类规则是：如果样本Y满足

　　　　　　　　　　　　　　

allsamples=[];
global pathname;
global Y;
global x;
global p;
global train_num;
global M;
global N;
M=112;%row
N=92;%column
train_num=200;
Gt=zeros(N,N);
pathname='C:\matlabworkspace\mypca\ORL\s';
for i=1:40
    suma=zeros(M,N);
        for j=1:5
            a=imread(strcat(pathname,num2str(i),'\',num2str(j),'.pgm'));
            a=double(a);
            suma=suma+a;
        end
            averageA=suma/5;
        for j=1:5
               a=imread(strcat(pathname,num2str(i),'\',num2str(j),'.pgm'));
               a=double(a);
              Gt=Gt+(a-averageA)'*(a-averageA);
        end
end

    Gt=Gt/train_num;
    
    [v d]=eig(Gt);
  for i=1:N
        dd(i)=d(i,i);
  end
    [d2 index]=sort(dd,'descend');
    
    cols=size(v,2)
   for i=1:cols
        dsort(:,i)=v(:,index(i));
   end
  
   dsum=sum(dd);
   dsum_extract=0;
  
   p=0;
   while(dsum_extract/dsum<0.8)
   p=p+1;
   dsum_extract=dsum_extract+dd(p);
   end
  x=dsort(:,1:p);
 x
  p
  size(x)
 Y=cell(40);
  for  i=1:40
      tempA=zeros(M,N);
      for j=1:5
          a=imread(strcat(pathname,num2str(i),'\',num2str(j),'.pgm'));
          a=double(a);
          tempA=tempA+a;
      end
      tempA=tempA/5;
      Y(i)=mat2cell(tempA*x);
  end
  
 %test course
 
 accu=0;
 for i=1:40
     for j=6:10
     a=imread(strcat(pathname,num2str(i),'\',num2str(j),'.pgm'));
     a=double(a);
     tempY=a*x;
     tempindex=1;
     tempsum=10000000;
     for k=1:40
         sumlast=0.0;
         YY=cell2mat(Y(k));
         
          for l=1:p
             sumlast=sumlast+norm(tempY(:,l)-YY(:,l));
          end
          
          if(tempsum>sumlast)
              tempsum=sumlast;
              tempindex=k;
          end
     end
     if tempindex==i
         accu=accu+1;
     end
     end
 end
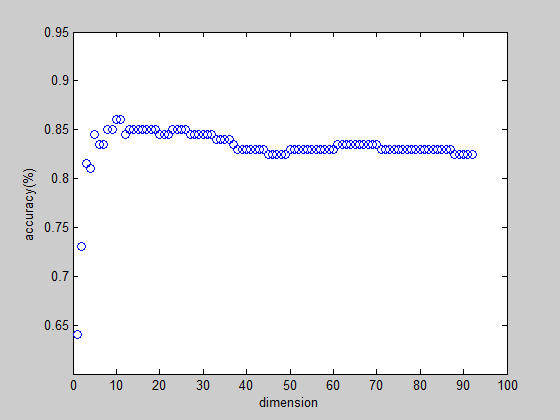
     accuracy=accu/200
          

结果：