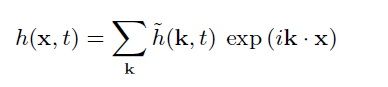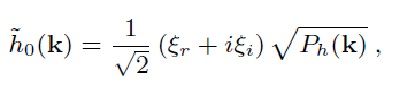Simulating Ocean Water

http://graphics.ucsd.edu/courses/rendering/2005/jdewall/tessendorf.pdf

siggraph 2001的一篇文章，后面很多关于水的文章都要提到，经典之作。

文章参杂数学概念比较多，与spherical harmonics相关的不相上下，对于数学基础不是那么强的我来说，着实花费了些力气查阅文档。

数学方面理解还很有限，尽量笔记和理解吧。

 

 

文中记录的关于光影方面的效果暂且跳过。

主要关注水的geometry方面的simulation。

 

水的FFT的simulation即便不是很了解，起码名字是很熟悉的。

本文从介绍一些相对更轻口味的数学的模拟方法开始，内含一些重要的概念。

 

 

GerstnerWaves

 

这是一个很早提出的对于水的一个模拟，核心是利用一些sin， cos来模拟水。

细节不是那么重要，关键点几个概念，除了sin,cos这些周期函数的模拟，相关参数比较重要的是水流动的速度与水的波长的一个关系：

：k为水流速度，lemda是波长。

 

然后可以用多组sin，cos函数来结合一个更加复杂也更加自然的水。

 

这种方法现在在一些游戏里面也还是有市场的。

 

 

Dispersion Relation

 

这部分讨论的是水的频率与水的几个特性的关系。

w是频率，g是重力加速度，k是水的流动速度。他们之间在深水区有这么个关系。

 

d是水深，在浅水区，频率和这些参数有关系的。

对于很小的水波，需要考虑到水的张力（tenssor)，就是L，频率是这么个关系。

 

 

 

Statical(统计的）wave model and fourier transform

 

几个概念先列一下：

傅立叶展开，http://en.wikipedia.org/wiki/Fourier_series

指周期函数可以展开成一系列三角函数的和：

实际定义要有更多的条件，略过，基本含义是这样的。

这样就把可能非常复杂的周期函数化成我们熟悉的三角函数，何况三角函数还有那么多的特性，分析起来有优势多了。

 

傅立叶变换：http://en.wikipedia.org/wiki/Fourier_transform

http://wenku.baidu.com/view/e3b7f0fdc8d376eeaeaa3187.html

具体数学推理是很麻烦的公式。

 

物理含义方面，这个在信号处理方面有着很广泛的应用，是将一个时域上的函数转换到频域上来表示。

比如我们看sin(t)+cos(2t)这个函数，画出来一个波浪线相对麻烦，但是用频域来表示就简单多了。

另外一种是IFFT(Inverse Fast Fourier Transform)，也就是逆傅立叶变换，就是频域转到时域。

物理现象中常常出现的情况是时域中非常复杂的东西，在频域中就很简单，反之亦然。

 

那么换做水，我们所见的水高低起伏是时域上高度的一个变化（当然也有位置的关系）。

那么切换到频域表示之后，我们就可以结合前面的关于频率的介绍，根据水的流速，张力等情况算出频率，进而将水的高低起伏通过这些表达清楚。

 

离散傅立叶变换：

http://zh.wikipedia.org/zh/%E7%A6%BB%E6%95%A3%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2#.E5.BF.AB.E9.80.9F.E5.82.85.E9.87.8C.E5.8F.B6.E5.8F.98.E6.8D.A2

上面说到的都是针对连续函数来说的。

但是实际生活中，数字化的信号都是离散的信号，这时候进行处理的话就需要针对离散函数做傅立叶变换，获得频域上的新的函数表示。

这点图形学上比较熟悉的应该是jpeg压缩，因为人眼对高频数据敏感度不高，所以对离散傅立叶变换的函数滤掉高频数据，剩下低频数据进行压缩。这个是离散傅立叶变换的一个典型例子。

 

快速傅立叶变换：

http://zh.wikipedia.org/zh-cn/%E5%BF%AB%E9%80%9F%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2

快速傅立叶变换是针对离散傅立叶变换来说的，离散傅立叶变换计算仍旧是比较慢，牛人们开发出一些快速算法统称快速傅立叶变换。

 

 

 

文中提到这个快速傅立叶变换不是基于实际物理模型，而是基于统计的。

那么应该是进行数字采样之后，进行统计归纳的一个结果。

 

所以最后说下来是fft是一个可以很真实描述水的数学模型，这个模型来自观察而不是实际物理推算，模型公式为：

这里k是2维vector，编程中就是指grid中sample的点，这个和离散傅立叶变换的采样点相对应。

 

浪线h是重点，这个函数描述了从space domain转到frequency domain，在特定frequency----(i*dot(k,x))下的amplitude。这个直接决定了水的高度分布，如果h~(k,t)就是一个常数*exp(i*w(t))的话，就是很平均的一个水波形状。如果是下面介绍的philips spectrum，那就是一个深海中水波的分布形状。

 

philips spectrum:

然后2公式连发，可以看出浪线h(k,t)是什么了：

 

这样下来一个完整的数学模型就ok了。

这里需要注意每一个的条件和意义，否则coding的时候会被恶心到。

第一个h~(k)那个，走丝r和走丝i是随机数，要求平均值是0，方差小于1，自己实现的时候平均值没有采对，结果出的乱七八糟的结果，囧。

phillips spectrum里面的和L相乘的k应该是wave number，这个到处没有找到确切的物理意义，论文本身也是说的很含糊，ati文章里有提到，所以我就顺着走，出来效果是属于比较平淡的湖水。

然后按照我最先理解的是k就是2d vector，k平方就是k dot k这种，最后做出来是深海的浩翰感觉。

非常赞。

所以这样看来，phillips spectrum本身作为一个波普，我们本身也可以尝试各种波普，来创造出各种有意思的水了。

 

 

 

其他的choppywave，reflection， refraction，caustic，godray都比较熟悉了，直接跳过。