zoj 3195 Design the city 【LCA转RMQ】 【求三点最短距离】
Cerror is the mayor of city HangZhou. As you may know, the traffic system of this city is so terrible, that there are traffic jams everywhere. Now, Cerror finds out that the main reason of them is the poor design of the roads distribution, and he want to change this situation.
In order to achieve this project, he divide the city up to N regions which can be viewed as separate points. He thinks that the best design is the one that connect all region with shortest road, and he is asking you to check some of his designs.
Now, he gives you an acyclic graph representing his road design, you need to find out the shortest path to connect some group of three regions.
Input
The input contains multiple test cases! In each case, the first line contian a interger N (1 < N < 50000), indicating the number of regions, which are indexed from 0 to N-1. In each of the following N-1 lines, there are three interger Ai, Bi, Li (1 < Li < 100) indicating there's a road with length Li between region Ai and region Bi. Then an interger Q (1 < Q < 70000), the number of group of regions you need to check. Then in each of the following Q lines, there are three interger Xi, Yi, Zi, indicating the indices of the three regions to be checked.
Process to the end of file.
Output
Q lines for each test case. In each line output an interger indicating the minimum length of path to connect the three regions.
Output a blank line between each test cases.
Sample Input
4 0 1 1 0 2 1 0 3 1 2 1 2 3 0 1 2 5 0 1 1 0 2 1 1 3 1 1 4 1 2 0 1 2 1 0 3
Sample Output
3 2 22
题意:给定N个点,下面N-1行u、v、d表示一条无向边和边权值,它们构成了一棵无向树。现在给出Q查询。问在树上连通a、b、c三点的最短距离。
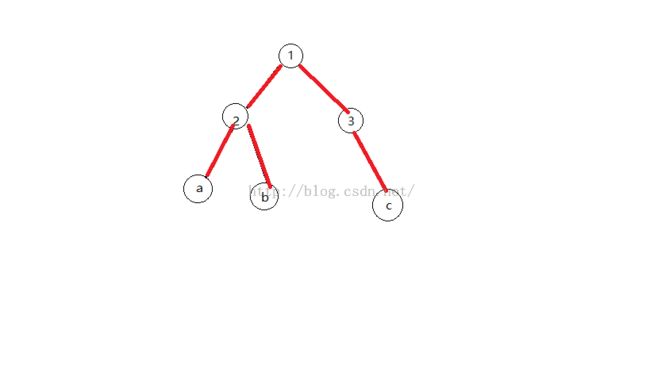
上图:
显然在树上连通a、b、c三点最短距离
为dist[a] + dist[b] + dist[c] - (dist[LCA(a, b)] + dist[LCA(a, c)] + dist[LCA(b, c)])。其中dist[]存储节点到根的最短距离。
AC代码:注意输出格式!!!
#include <cstdio> #include <cstring> #include <algorithm> #define MAXN 50000+100 using namespace std; struct Edge { int from, to, val, next; }; Edge edge[MAXN<<1]; int head[MAXN], edgenum; int vs[MAXN<<1]; int depth[MAXN<<1]; int id[MAXN]; int dist[MAXN]; int dfs_clock; int N, Q; void init() { edgenum = 0; memset(head, -1, sizeof(head)); } void addEdge(int u, int v, int w) { Edge E = {u, v, w, head[u]}; edge[edgenum] = E; head[u] = edgenum++; } void getMap() { int a, b, c; for(int i = 1; i < N; i++) { scanf("%d%d%d", &a, &b, &c);//点是从0开始编号的 a++, b++; addEdge(a, b, c), addEdge(b, a, c); } } void DFS(int u, int fa, int d) { id[u] = dfs_clock; vs[dfs_clock] = u; depth[dfs_clock++] = d; for(int i = head[u]; i != -1; i = edge[i].next) { int v = edge[i].to; if(v == fa) continue; dist[v] = dist[u] + edge[i].val; DFS(v, u, d+1); vs[dfs_clock] = u; depth[dfs_clock++] = d; } } void find_depth() { memset(vs, 0, sizeof(vs)); memset(id, 0, sizeof(id)); memset(depth, 0, sizeof(depth)); memset(dist, 0, sizeof(dist)); dfs_clock = 1; DFS(1, -1, 0); } int dp[MAXN<<1][30]; void RMQ_init(int NN) { for(int i = 1; i <= NN; i++) dp[i][0] = i; for(int j = 1; (1<<j) <= NN; j++) { for(int i = 1; i + (1<<j) - 1 <= NN; i++) { int a = dp[i][j-1]; int b = dp[i + (1<<(j-1))][j-1]; if(depth[a] <= depth[b]) dp[i][j] = a; else dp[i][j] = b; } } } int query(int L, int R) { int k = 0; while((1<<(k+1)) <= R-L+1) k++; int a = dp[L][k]; int b = dp[R - (1<<k) + 1][k]; if(depth[a] <= depth[b]) return a; else return b; } int LCA(int u, int v) { int x = id[u]; int y = id[v]; if(x < y) return vs[query(x, y)]; else return vs[query(y, x)]; } void solve() { int a, b, c; scanf("%d", &Q); while(Q--) { scanf("%d%d%d", &a, &b, &c); a++, b++, c++; printf("%d\n", dist[a] + dist[b] + dist[c] - (dist[LCA(a, b)] + dist[LCA(a, c)] + dist[LCA(b, c)])); } } int main() { int t = 0;//注意输出格式 while(scanf("%d", &N) != EOF) { if(t > 0) printf("\n"); init(); getMap(); find_depth(); RMQ_init(dfs_clock - 1); solve(); t++; } return 0; }