希尔伯特向量空间中的信号

希尔伯特空间又叫完备的内积空间，是有限维欧几里得空间的一个推广。

一段连续信号可以视为一个无限维度的向量，有无限个正交基，相应的，离散的可以视为有限维度的向量。

内积：<x,y>=[x0*,x1*,...] * [y0,y1,...]T

两个向量正交，等价于内积为0.

模为一的正交基称为标准正交基（othonormal）。

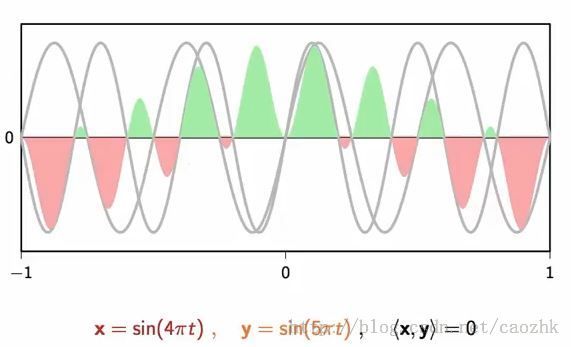
对于两个有公共基频的正弦波信号，可以画出二者的乘积，可以看到乘积信号每一段x轴之上的，都有一段x轴之下的对应，因此内积为0.

毕达哥拉斯定理：||x+y||^2=||x||^2+||y||^2，如果x,y垂直。由此可以得出，两正交信号之和的能量为二者能量之和。

MSE其实指的是两个代表信号的向量之差delat计算得出的||delta||^2，即对差的平方积分。

希尔伯特空间要求完备性，即两个向量运算的结果仍然属于此空间。

例如，有理数的集合中sum(n=0,...oo)(1/n!)=e，不属于有理数。

帕斯瓦尔定理

如果一个信号可以表示成一组正交基的组合，那么它的能量等于这些正交基分量的权重的平方和。

如果x=x1+x2，则很明显上述结论成立。把毕达哥拉斯定理推广到多维空间就可以得到上述结论。

斯密特正交化

对于指数正交基，[1,t,t^2,...]，每个函数都可以在此基上展开。

如sint在[-1，1]上，相应的正交基是指数基的一种变幻，即[sqrt(1/2),sqrt(3/2)*t,...]。在整个x轴上面的正交基是不同的。