HDU 1401 Solitaire
Solitaire
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 65536/32768K (Java/Other)
Total Submission(s) : 12 Accepted Submission(s) : 1
Problem Description
Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).
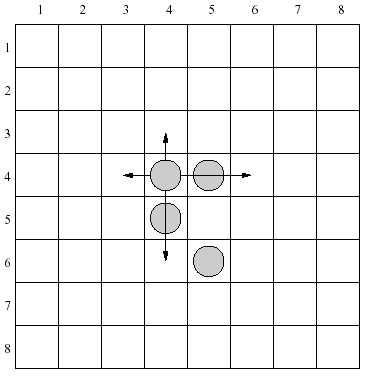
There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).

There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
Input
Each of two input lines contains 8 integers a1, a2, ..., a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file.
Output
The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.
Sample Input
4 4 4 5 5 4 6 5 2 4 3 3 3 6 4 6
Sample Output
YES
Source
Southwestern Europe 2002
双向广搜。 每组棋子的坐标为1~8 共有四个坐标 8个数都可以用三个二进制数保存 所以可以将状态转换为相应的十进制数进行状态压缩
只能走八步,每步有十六中变化 所以双向广搜可以解决
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<map>
#include<algorithm>
using namespace std;
struct Point
{
int x,y;
bool cheak()
{
if(x>=0&&x<8&&y>=0&&y<8)
return true ;
else return false ;
}
};
struct node
{
Point a[5];
int t;
} st,ed,e;
int dir[4][2]= {0,1,0,-1,1,0,-1,0};
bool vis[16777216+1]; //标记 状态压缩
int us[65536+10]; //记录出现过的状态
int len;
bool cmp(Point n1,Point n2)
{
return n1.x!=n2.x?n1.x<n2.x:n1.y<n2.y;
}
int get_hash(Point *tmp) //状态压缩
{
int res=0;
sort(tmp,tmp+4,cmp);
for(int i=0; i<4; i++)
{
res|=(tmp[i].x<<(6*i));
res|=(tmp[i].y<<(6*i+3));
}
return res;
}
bool fine(int num) //二分查找
{
int l=0,r=len-1;
while(l<=r)
{
int mid=(l+r)/2;
if(num==us[mid]) return true ;
if(num>us[mid])
l=mid+1;
else r=mid-1;
}
return false ;
}
void dfs()
{
queue<node>q;
memset(vis,false ,sizeof(vis));
len=0;
int Hash;
Hash=get_hash(st.a);
vis[Hash]=true ;
us[len++]=Hash;
st.t=0;
q.push(st);
int k;
//起点开始广搜可以出现的状态
while(q.size())
{
st=q.front();
q.pop();
if(st.t>=4) continue ;
for(int j=0; j<4; j++)
{
for(int i=0; i<4; i++)
{
e=st;
e.t++;
e.a[i].x+=dir[j][0];
e.a[i].y+=dir[j][1];
if(!e.a[i].cheak())
continue ;
for(k=0; k<4; k++)
{
if(k!=i&&e.a[k].x==e.a[i].x&&e.a[k].y==e.a[i].y)
break;
}
if(k==4)
{
Hash=get_hash(e.a);
if(!vis[Hash])
{
vis[Hash]=true ;
us[len++]=Hash;
q.push(e);
}
}
else
{
e.a[i].x+=dir[j][0];
e.a[i].y+=dir[j][1];
if(!e.a[i].cheak())
continue ;
for(k=0; k<4; k++)
{
if(k!=i&&e.a[k].x==e.a[i].x&&e.a[k].y==e.a[i].y)
break;
}
if(k==4)
{
Hash=get_hash(e.a);
if(!vis[Hash])
{
vis[Hash]=true ;
us[len++]=Hash;
q.push(e);
}
}
}
}
}
}
sort(us,us+len);
memset(vis,false ,sizeof(vis));
Hash=get_hash(ed.a);
if(fine(Hash)) //从起点走出现过这种状态
{
printf("YES\n");
return ;
}
vis[Hash]=true ;
q.push(ed);
while(q.size())
{
st=q.front();
q.pop();
if(st.t>=4) continue ;
for(int j=0; j<4; j++)
{
for(int i=0; i<4; i++)
{
e=st;
e.t++;
e.a[i].x+=dir[j][0];
e.a[i].y+=dir[j][1];
if(!e.a[i].cheak())
continue ;
for(k=0; k<4; k++)
{
if(k!=i&&e.a[k].x==e.a[i].x&&e.a[k].y==e.a[i].y)
break;
}
if(k==4)
{
Hash=get_hash(e.a);
if(fine(Hash))
{
printf("YES\n");
return ;
}
if(!vis[Hash])
{
vis[Hash]=true ;
q.push(e);
}
}
else
{
e.a[i].x+=dir[j][0];
e.a[i].y+=dir[j][1];
if(!e.a[i].cheak()) continue ;
for(k=0; k<4; k++)
{
if(k!=i&&e.a[k].x==e.a[i].x&&e.a[k].y==e.a[i].y)
break;
}
if(k!=4) continue ;
Hash=get_hash(e.a);
if(fine(Hash))
{
printf("YES\n");
return ;
}
if(!vis[Hash])
{
vis[Hash]=true ;
q.push(e);
}
}
}
}
}
printf("NO\n");
return ;
}
int main()
{
while(~scanf("%d%d",&st.a[0].x,&st.a[0].y))
{
for(int i=1; i<4; i++)
scanf("%d%d",&st.a[i].x,&st.a[i].y);
st.t=0;
for(int i=0; i<4; i++)
scanf("%d%d",&ed.a[i].x,&ed.a[i].y);
ed.t=0;
//将坐标转为0~7对应2^3-1的数 状态压缩
for(int i=0; i<4; i++)
{
st.a[i].x--;
st.a[i].y--;
ed.a[i].x--;
ed.a[i].y--;
}
dfs();
}
return 0;
}