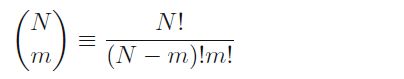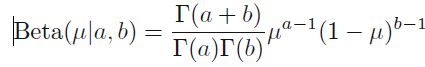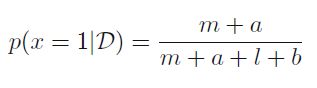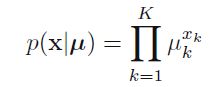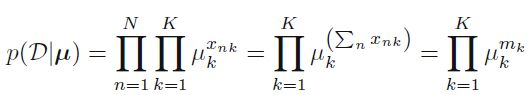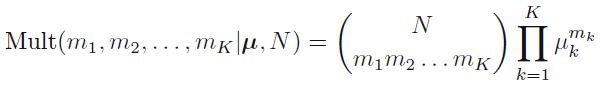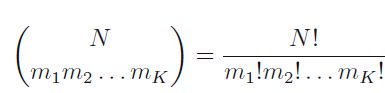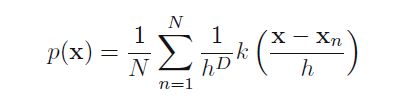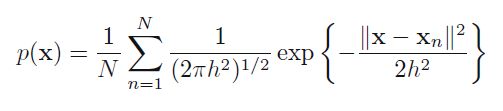PRML CHAPTER 2 学习笔记
BERNOULLI DISTRIBUTION &BINOMIAL DISTRIBUTION(贝努利分布&二元分布),个人觉得二元分布比二项分布来的更直观一些。
贝努利分布:投一个硬币出现的结果x=head=1,tail=0的概率分布,表达式如下
现在进行n次试验,观察到的结果(head or tail :0 or 1)由一个数据组组成D={X1,X2,.....Xn},根据贝努利的经验,我们有n次试验的似然函数的形式(每一次都是一次独立的试验,n次贝努利试验结果的乘积形式)
那么n次试验中,什么时候的u取最大值呢,对似然函数两遍同事取对数,并令其对u的导数=0,我们得到最大u值
若是只考虑出现头head的次数,那么有
m为出现头(head)的次数的总和
对于n次试验中,我们对于专门出现头的次数m,它也满足一个分布,于是二项分布由此处引出,
BETA DISTRIBUTION(贝塔分布)
不管是贝努利分布还是二项分布,都是基于观察head=1得出。那么当数据量过小,则容易出现过拟合(over-fitting),于是我们用贝叶斯的方法来解决这个问题,引入beta prior。
a,b为超参数,这两个家伙掌控u的分布。
在有了以上知识后,脑子里是否会浮现Posterior=Likelihood*Prior.将Beta()*Bin(),有如下式子:
正则化后,等式如下:
可以看到,后验概率于先验分布形式保持的非常好,前后一致。
贝叶斯理论的一个重要作用我们需要再这里发挥一下,就是预测下一步出现X=1的概率是多少,
对于无限大的数据组,m,l~~∞,P=m/N(最大似然的结果),当数据无穷大时,预测的结果的和极大似然函数处理的结果一致。换句话就是,在数据量无穷大的情况下,贝叶斯和频率派的表现是一样的。
对于有限的数组,预测值在最大似然函数u值和先验均值u之间。
Multinomial Distribution(多元分布)
做一次试验,可能出现2种可能的为贝努利分布(one of two possible values)。
现做一次试验,可能出现多种结果的分布的为多元分布(one of k possible values)。假设我们掷一个骰子(6面),只有第4次出现了我们想要的最大值,表示为X=(0, 0, 0, 1, 0, 0 )’,我们用u来代表出现x=1的概率分布,则有如下分布形式:
那么现在我们做n次试验,D=(X1,X2,...Xn),相应的似然函数如下:
同理,现在要求取最大的u值,两边取对数,并对u求导数,但是我们发现得出的结果为0,这一结果是不满足要求的,关键的时候,拉格朗日算子就隆重登场了,
经过计算,我们得到
考虑到做N次试验,其中m1,m2,...mk出现的联合概率且基于u分布表示为多元分布,表述如下:
对于多元分布的理解,N和k的关系需要细细琢磨
Dirichlet Distribution
多元分布的先验函数prior定义为Dirichlet ,表现形式如下:
同上述分析一样,我们得到后验形式:
正则化后
因为这个函数跟beta,gamma等一样,会比较难理解,详细解读请参见:http://en.wikipedia.org/wiki/Dirichlet_distribution
(以上内容整理于2013.1.20)
开始概率密度估计之前,弄清楚2个概念:CDF&PDF. 离散变量构成的分布----CDF(Culmulative density function),连续变量构成的分布----PDF(Probility density function)
通过一组数据中一部分参数构成满足某种形式的函数来描述概率密度分布形式 叫做参数化的概率密度估计。当从数据中提取的参数组成的函数模型不足以表达函数的形式时或者不具备较好的预测性,比如,如果从某种数据中产生的多元变量模型,那么通过一个高斯函数时无法描述此模型,因为高斯模型是一个连续的单一模型,多以此时引入非参数方法来进行函数密度估计。这里的PRML的非参数模型选择频率派的方法,非nonparametric bayesian model。
假设从一个D-dimentions 空间抽取一些未知概率密度函数P(x),我们运用Euclidean方法来估计p(x)。
考虑一个含有观察变量X的一个很小的区域R。现假设有N个观察变量的PDF为p(x),那么其中K个变量落入R中,这个过程满足二项分布,要么落入R,要么在R外。
对于比较大的N,大部分数据都集中在二项分布的均值处,E【K/N】=P,故落入R中K=NP.同时假设R足够的小,那么P(x)间接类似于一个常数在R中,于是有P=p(x)v (v表示空间R的体积),于是乎我们得出概率密度函数p(x)=K/NV.这个等式有2个未知参数,K与V。固定V值 ---核函数估计(kennel density estimator(paren window)),固定K值--K邻近法(KNN (K nearest neighbour))。
先看kennel density estimator,假设R是一个中心点为x的超球体,为方便计算落入区域中的K的个数,定义核函数K(u)={1,-0.5<=u<=0.5;0,otherwise},换成一个通俗的表达式就是落入边长为h,中心点为Xn的球体的值K((X-Xn)/h)=1.那么落入区域内K 的总数的表达式K=sigma K((X-Xn)/h)=1 for n=1 to N.估计出来的的概率密度函数是公式中的样子:
这里,V=h的D次方,见公式分母。(联想一下,面积是平方,体积是立方,超球体D维向量的V=h的D次方)
现在需要选择一个平滑的概率模型核函数,根据p(x)的样子,长的跟高斯类似,就是高斯了(也可以选择其它概率分布函数)。小变样子的核函数如下,
h代表高斯方差。
至此,我们的概率模型通过在所有的数据点中安放一个高斯函数并将所有的数据点相加再除以N (nomalized p(x))。
上图中,h的值的选定决订概率密度核函数对曲线表示的好坏。过大过小都不好,呵呵。在这个估计中,没有训练过程(无计算),核函数选定后,再不断探索哪个更好。此方法的一大弱点是,但是当数据量增大的时候,核函数的计算量也需要相应的跟着增大。
未完待续...