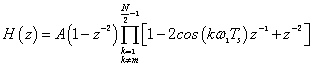信号处理小结（2）：滤波器

除了用基本滤波单元组成级联滤波器的方法外，在数字保护中用得较多的就是用零、极点配置法设计数字滤波器。它通过直接在Z平面上合理地设置零点和极点，以得到合乎要求的频率响应特性和时延特性。

一、全零点滤波器

在转移函数中只含有零点而无极点。假定N为偶数，要求除k=m次谐波外，完全滤除直流、N/2次及其它各次谐波。

 

二、狭窄带通滤波器

除了考虑必要的零点外，在需要滤取得频率处再设置一个合适的极点。如使r很接近1，就可以获得很窄的通带和比较陡峭的过渡带。

为距离保护设计一个狭窄带通滤波器。要求完全抑制直流和N/2次谐波分量，并比较采样频率fs、极点的极径r=p对滤波特性的影响。

滤波器的转移函数为

p越接近1，幅频特性曲线越窄越陡，因此p的取值与滤波器滤除非基频分量的能力成正比变化。

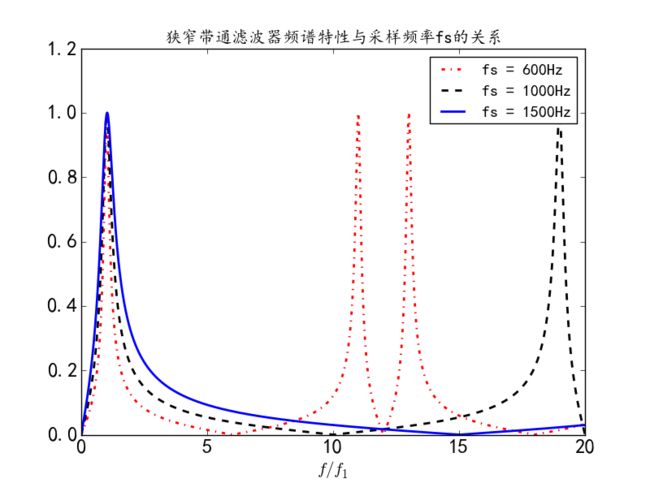
设p=0.95。有图可见，随fs增大，滤波器滤除非基频分量能力下降。这是由于位于高频处的零点对应于N/2次谐波，当fs越低，N/2次谐波分量就越靠近基频。但fs越低，对模拟低通滤波器的要求越苛刻，或者说越容易出现混叠现象。

## 全零点滤波器
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from pylab import *

mpl.rcParams['font.sans-serif'] = 'KaiTi'
mpl.rcParams['axes.unicode_minus'] = False

n = np.arange(0,6, 0.0002)
N = 12
z = np.exp(2*np.pi*n/N*1j)

##f = (1-z**(-8))**2*(1-z**(-10))/(1-z**(-12))
Hb = ( 1+z**(-2)-z**(-6)-z**(-8))
Hb1 = ( 1+z**(-2)-z**(-6)-z**(-8))*( 1+np.sqrt(3)*z**(-1)+z**(-2))
Hs = ( 1-z**(-3)+z**(-6)-z**(-9))
Hs1 = ( 1-z**(-3)+z**(-6)-z**(-9))*( 1+z**(-1))
magHb = np.abs(Hb)
magHb1 = np.abs(Hb1)
magHs = np.abs(Hs)
magHs1 = np.abs(Hs1)

plt.figure(1)
plt.plot(n, magHb/np.max(magHb), label=u"简化的基波滤波器幅频特性", lw=2)
plt.plot(n, magHb1/np.max(magHb1), '--', label=u"基波滤波器幅频特性", lw=2)
plt.xlabel(r"$f/f_1$", fontsize=15)
plt.xticks(fontsize=18); plt.yticks(fontsize=18)
plt.title(r"$H_b=(1+z^{-2}-z^{-6}-z^{-8})( 1+\sqrt{3}z^{-1}+z^{-2})$", fontsize=15)
plt.legend()
plt.figure(2)
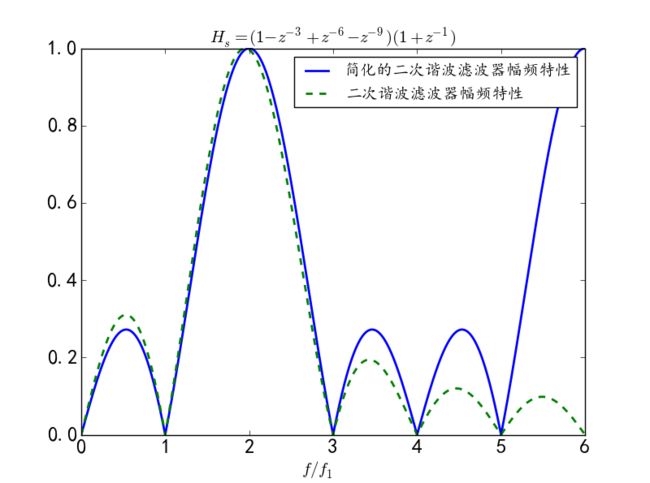
plt.plot(n, magHs/np.max(magHs), label=u"简化的二次谐波滤波器幅频特性", lw=2)
plt.plot(n, magHs1/np.max(magHs1), '--', label=u"二次谐波滤波器幅频特性", lw=2)
plt.xlabel(r"$f/f_1$", fontsize=15)
plt.xticks(fontsize=18); plt.yticks(fontsize=18)
plt.title(r"$H_s=(1-z^{-3}+z^{-6}-z^{-9})( 1+z^{-1})$", fontsize=15)

plt.legend()
plt.show()

## 狭窄带通滤波器
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from pylab import *

mpl.rcParams['font.sans-serif'] = 'KaiTi'
mpl.rcParams['axes.unicode_minus'] = False

n = np.arange(0,20, 0.0001)
w1 = 2*np.pi*50
fs = np.array([600, 1000, 1500])
N = fs/50
z = np.exp(2*np.pi*n/N[1]*1j)
Ts = [1.0/600, 1.0/1000, 1.0/1500]

plt.figure(1)
line_style = ['r-.', 'k--', '-']
line_label = ['p = 0.969', 'p = 0.936', 'p = 0.910']
p = [0.969, 0.936, 0.910]
i = 0
for p in [0.969, 0.936, 0.910]:
    Hz = ( 1-z**(-2) ) / ( 1-2*p*np.cos(w1*Ts[1])*z**(-1)+p**2*z**(-2) )
    magHz = np.abs(Hz)
    if i==0:
        max_mag = np.max(magHz)
    plt.plot(n, magHz/max_mag, line_style[i], lw=2, label=line_label[i])
    i += 1
plt.xticks(fontsize=18); plt.yticks(fontsize=18)
plt.xlabel(r"$f/f_1$", fontsize=15)
plt.title(u"狭窄带通滤波器频谱特性与参数p的关系", fontsize=15)
plt.legend()

plt.figure(2)
p = 0.95
for i in [0, 1, 2]:
    z = np.exp(2*np.pi*n/N[i]*1j)
    Hz = ( 1-z**(-2) ) / ( 1-2*p*np.cos(w1*Ts[i])*z**(-1)+p**2*z**(-2) )
    magHz = np.abs(Hz)
    if i==0:
        max_mag = np.max(magHz)
    plt.plot(n, magHz/max_mag, line_style[i], lw=2, label=('fs = '+str(fs[i])+'Hz'))
plt.xticks(fontsize=18); plt.yticks(fontsize=18)
plt.xlabel(r"$f/f_1$", fontsize=15)
plt.title(u"狭窄带通滤波器频谱特性与采样频率fs的关系", fontsize=15)
plt.legend()
plt.show()