模糊聚类算法（FCM）和硬聚类算法（HCM)的VB6.0实现及其应用

程序实现：

    上面的公式看似复杂，其实我们关心的就是最后的5个计算步骤，这里说明一下，有的书上以隶属度矩阵的某一范数小于一定值作为收敛的条件，这也可，不过计算量稍微要大一点了。

        程序采用VB6.0编制，完全按照以上的步骤进行。

    

'程序实现功能：模糊聚类和硬聚类
'作    者： laviewpbt
'联系方式： [email protected]
'QQ:33184777
'版本：Version 2.3.1
'说明：复制请保留源作者信息，转载请说明，欢迎大家提出意见和建议

Private Declare Function GetTickCount Lib "kernel32" () As Long

Private Enum IniCenterMethod    '初始中心的方法
    CreateRandom                '随机的中心点
    CreateByHcm                 '由HCM创建的中心点
    CreateByRandomZadeh         '先随机创建隶属矩阵，然后计算得到的中心点

    CreateByHand                '手工确定初始中心点

End Enum

Private Enum AntiFuzzyMethod    '反模糊的方法
    Max                         '最大隶属度法
    Middle                      '中位数法
    Mean                        '加权均值法
End Enum

Private Type FcmInfo
     Center() As Double         '聚类中心
     Degree() As Double         '隶属度，为Double类型
     Class() As Byte            '记录数据属于那一类
     TimeUse As Long            '所用时间
     Iterations  As Long        '迭带次数
     ErrMsg As String           '错误信息
End Type

Private Type HcmInfo
    Center() As Double          '聚类中心
    Class() As Byte             '记录数据属于那一类
    TimeUse As Long             '所用时间
    Iterations  As Long         '迭带次数
    ErrMsg As String            '错误信息
End Type

'*************************************************************************************
'*    作    者 ：    laviewpbt
'*    函 数 名 ：    Fcm
'*    参    数 ：    Data     -   待分类的样本，第一维的大小表示样本的个数，
'*                                第二维的大小表示样本的维数
'*                   Cluster  -   分类数
'*                   CreateIniCenter - 初始聚类中心的创建方法
'*                   AntiFuzzy -  反模糊化的方法
'*                   Exponent  -  一个控制聚类效果的参数，一般取2
'*                   Maxiterations  - 最大的迭代次数
'*                   MinImprovement - 最小的改进参数（两次迭代间聚类中心的距离）
'*    返回值 ：      FcmInfo结构，记录了相关的参数
'*    功能描述 ：    利用模糊理论的聚类方法把数据分类
'*    日    期 ：    2004-10-27 10.25.32
'*    修 改 人 ：    laviewpbt
'*    日    期 ：    2006-11-7 19.25.31
'*    版    本 ：    Version 2.3.1
'**************************************************************************************

Private Function Fcm(ByRef Data() As Double, ByVal Cluster As Long, Optional ByVal CreateIniCenter As IniCenterMethod = IniCenterMethod.CreateByHcm, Optional AntiFuzzy As AntiFuzzyMethod = Max, Optional Exponent As Byte = 2, Optional Maxiterations As Long = 400, Optional MinImprovement As Double = 0.01, Optional ByRef CenterByHandle As Variant) As FcmInfo
    If ArrayRange(Data) <> 2 Then
        Fcm.ErrMsg = "数据只能为二维数组"
        Exit Function
    End If
    Dim i As Long, j As Long, k As Long, l As Long, m As Long
    Dim DataNumber As Long, DataSize As Long
    Dim Temp As Double, Sum1 As Double, Sum2 As Double, Sum3 As Double, Index As Integer
    Dim OldCenter() As Double
    Fcm.TimeUse = GetTickCount
    DataNumber = UBound(Data, 1): DataSize = UBound(Data, 2)
    ReDim Fcm.center(1 To Cluster, 1 To DataSize) As Double
    ReDim Fcm.Degree(1 To Cluster, 1 To DataNumber) As Double
    ReDim Fcm.Class(1 To DataNumber) As Byte
    ReDim OldCenter(1 To Cluster, 1 To DataSize) As Double
    On Error GoTo ErrHandle:
    Randomize
    If CreateIniCenter = CreateRandom Then
        For i = 1 To Cluster
            For j = 1 To DataSize
                OldCenter(i, j) = Data(Rnd * DataNumber, j)    '产生随机初始中心点
            Next
        Next
    ElseIf CreateIniCenter = CreateByHcm Then
        Dim HcmCenter As HcmInfo
        HcmCenter = Hcm(Data, Cluster)
        For i = 1 To Cluster
            For j = 1 To DataSize
                OldCenter(i, j) = HcmCenter.center(i, j)   '产生HCM初始中心点
            Next
        Next
    ElseIf CreateIniCenter = CreateByRandomZadeh Then
        ReDim RndDegree(1 To Cluster, 1 To DataNumber) As Double
        Dim RndSum As Double
        For i = 1 To Cluster
            For j = 1 To DataNumber
                RndDegree(i, j) = Rnd           '创建随机的隶属度
            Next
        Next
        For j = 1 To DataNumber
            RndSum = 0
            For i = 1 To Cluster
                RndSum = RndSum + RndDegree(i, j)
            Next
            For i = 1 To Cluster
                RndDegree(i, j) = RndDegree(i, j) / RndSum   '隶属度矩阵每列之后必须为1
            Next
        Next
       
        For i = 1 To Cluster
            For j = 1 To DataSize
                Sum1 = 0: Sum2 = 0
                For k = 1 To DataNumber
                    Temp = Exp(Log(RndDegree(i, k)) * Exponent)  '其实就是RndDegree(i, k)^Exponent
                    Sum1 = Sum1 + Temp * Data(k, j)           '隶属度的平方乘以数值
                    Sum2 = Sum2 + Temp                        '隶属度的和
                Next
                OldCenter(i, j) = Sum1 / Sum2                 '得到聚类中心
            Next
        Next
    ElseIf CreateIniCenter = CreateByHand Then
        If IsMissing(CenterByHandle) Then
            Fcm.ErrMsg = "请提供初始聚类中心。."
            Exit Function
        ElseIf UBound(CenterByHandle, 1) <> Cluster Or UBound(CenterByHandle, 2) <> DataSize Then
            Fcm.ErrMsg = "手工提供的初始聚类中心维数有错误."
            Exit Function
        End If
        For i = 1 To Cluster
            For j = 1 To DataSize
                OldCenter(i, j) = CenterByHandle(i, j)
            Next
        Next
    End If

    
    Do
        Fcm.Iterations = Fcm.Iterations + 1
        For i = 1 To Cluster
            For j = 1 To DataNumber
                Sum1 = 0: Sum3 = 1
                For k = 1 To DataSize
                    Temp = Data(j, k) - OldCenter(i, k)
                    Sum1 = Sum1 + Temp * Temp             '计算第j点到第i个聚类中心的距离
                Next
                If Sum1 = 0 Then
                    Fcm.Degree(i, j) = 1                      '如果j点与第i个聚类中心重合，则完全属于该类
                Else
                    For k = 1 To Cluster
                        Sum2 = 0
                        If k <> i Then
                            For l = 1 To DataSize
                                Temp = Data(j, l) - OldCenter(k, l)
                                Sum2 = Sum2 + Temp * Temp  '计算第j点到其他聚类中心的距离
                            Next
                            Sum3 = Sum3 + Exp(Log(Sum1 / Sum2) * (2 / (Exponent - 1)))      '计算累加值,
                        End If
                    Next
                    Fcm.Degree(i, j) = 1 / Sum3    '计算新的隶属度
                End If
            Next
        Next
       
        For i = 1 To Cluster
            For j = 1 To DataSize
                Sum1 = 0: Sum2 = 0
                For k = 1 To DataNumber
                    Temp = Exp(Log(Fcm.Degree(i, k)) * Exponent)
                    Sum1 = Sum1 + Temp * Data(k, j)           '隶属度的平方乘以数值
                    Sum2 = Sum2 + Temp                        '隶属度的和
                Next
                Fcm.Center(i, j) = Sum1 / Sum2                    '得到新的聚类中心
            Next
        Next
       
        Temp = 0
        For i = 1 To Cluster
            For j = 1 To DataSize
                Temp = Temp + (OldCenter(i, j) - Fcm.Center(i, j)) ^ 2      ' 计算两次迭代之间的聚类中心的距离
                OldCenter(i, j) = Fcm.Center(i, j)                          ' 保留上一次的聚类中心
            Next
        Next

    Loop While Fcm.Iterations < Maxiterations And Temp > MinImprovement
   
    If AntiFuzzy = Max Then
        For i = 1 To DataNumber
            Temp = -1
            For k = 1 To Cluster
                If Temp < Fcm.Degree(k, i) Then    '得到列方向的最大值
                    Temp = Fcm.Degree(k, i)
                    Index = k
                End If
            Next
            Fcm.Class(i) = Index                  'Index记录了列方向最大隶属度的类
        Next
    ElseIf AntiFuzzy = Mean Then
         For i = 1 To DataNumber
             Temp = 0
             For j = 1 To Cluster
                Temp = Temp + Fcm.Degree(j, i) * j   '去隶书乘以对应的类别数之和
             Next
             Fcm.Class(i) = CInt(Temp)
      Next
    ElseIf AntiFuzzy = Middle Then
        For i = 1 To DataNumber
            Temp = 0
            For j = 1 To Cluster
                If Temp <= 0.5 And Temp + Fcm.Degree(j, i) >= 0.5 Then
                    Index = j
                    Exit For
                Else
                    Temp = Temp + Fcm.Degree(j, i)   '取面积的一半处
                End If
            Next
            Fcm.Class(i) = Index
        Next
    End If
    Fcm.TimeUse = GetTickCount - Fcm.TimeUse
    Exit Function
ErrHandle:
    Fcm.ErrMsg = Err.Description
    Fcm.TimeUse = GetTickCount - Fcm.TimeUse
End Function

'*************************************************************************************
'*    作    者 ：    laviewpbt
'*    函 数 名 ：    Hcm
'*    参    数 ：    Data     -   待分类的样本，第一维的大小表示样本的个数，
'*                                第二维的大小表示样本的维数
'*                   Cluster  -   分类数
'*                   Maxiterations  - 最大的迭代次数
'                    MinImprovement - 最小的改进参数（两次迭代间聚类中心的距离）
'*    返回值 ：      HcmInfo结构，记录了相关的参数
'*    功能描述 ：    直接利用硬聚类方法把数据分类
'*    日    期 ：    2004-10-24 20.10.56
'*    修 改 人 ：    laviewpbt
'*    日    期 ：    2006-11-7 20.11.23
'*    版    本 ：    Version 2.3.1
'**************************************************************************************

Private Function Hcm(ByRef Data() As Double, ByVal Cluster As Byte, Optional Maxiterations As Long = 400, Optional MinImprovement As Double = 0.01) As HcmInfo
    If ArrayRange(Data) <> 2 Then
        Hcm.ErrMsg = "数据只能为二维数组"
        Exit Function
    End If
    Dim i As Long, j As Long, k As Long, l As Long, m As Long
    Dim DataNumber As Long, DataSize As Long
    Dim Temp As Double, DX As Double, DY As Double, SumValue() As Double, SumNumber() As Long
    Dim OldCenter() As Double, Distance As Double, Dist As Double, Index As Long
    On Error GoTo ErrHandle:
    Hcm.TimeUse = GetTickCount
    DataNumber = UBound(Data, 1): DataSize = UBound(Data, 2)
    ReDim Hcm.Center(1 To Cluster, 1 To DataSize) As Double
    ReDim Hcm.Class(1 To DataNumber) As Byte
    ReDim OldCenter(1 To Cluster, 1 To DataSize) As Double
    For i = 1 To Cluster
        For j = 1 To DataSize
            OldCenter(i, j) = Data(i * DataNumber / Cluster, j) '产生初始中心点
        Next
    Next
    Do
        Hcm.Iterations = Hcm.Iterations + 1
        ReDim SumNumber(Cluster) As Long
        ReDim SumValue(Cluster, DataSize) As Double
        For i = 1 To DataNumber
            Distance = 40000000000#
            For j = 1 To Cluster
                Dist = 0
                For k = 1 To DataSize
                    Temp = Data(i, k) - OldCenter(j, k)
                    Dist = Dist + Temp * Temp             '计算第j点到第i个聚类中心的距离
                Next
                If Distance > Dist Then
                    Distance = Dist
                    Index = j                         '把i点归于距离该点最近的中心点所在的类
                End If
            Next
            Hcm.Class(i) = Index
            For j = 1 To DataSize
                SumValue(Index, j) = SumValue(Index, j) + Data(i, j)
            Next
            SumNumber(Index) = SumNumber(Index) + 1
        Next
       
        For i = 1 To Cluster
            For k = 1 To DataSize
                If SumNumber(i) = 0 Then
                    Hcm.Center(i, k) = Data(Rnd * DataNumber, k)
                Else
                    Hcm.Center(i, k) = SumValue(i, k) / SumNumber(i)         '求新的中心
                End If
            Next
        Next
        Temp = 0
        For i = 1 To Cluster
            For j = 1 To DataSize
                Temp = Temp + (OldCenter(i, j) - Hcm.Center(i, j)) ^ 2      ' 计算两次迭代之间的聚类中心的距离
                OldCenter(i, j) = Hcm.Center(i, j)                          ' 保留上一次的聚类中心
            Next
        Next
    Loop While Hcm.Iterations < Maxiterations And Temp > MinImprovement
    Hcm.TimeUse = GetTickCount - Hcm.TimeUse
    Exit Function
ErrHandle:
    Hcm.ErrMsg = Err.Description
    Hcm.TimeUse = GetTickCount - Hcm.TimeUse
    End Function

 

'*************************************************************************************
'*    作    者 ：    网络
'*    函 数 名 ：    ArrayRange
'*    参    数 ：    Data     -   待测试的数据
'*    返回值 ：      返回数组的维数
'*    日    期 ：    2006-7-10 13.20.40
'*    修 改 人 ：    laviewpbt
'*    日    期 ：    2006-11-7 10。10。45
'*    版    本 ：    Version 1.2.1
'**************************************************************************************
Public Function ArrayRange(Data() As Double) As Integer
    Dim i As Integer, ret As Integer
    Dim ErrF As Boolean
    ErrF = False
    On Error GoTo ErrHandle
    For i = 1 To 60               'VB中数组最大为60
        ret = UBound(mArray, i)   '用UBound函数判断某一维的上界，如果大数组的实际维数时产生超出范围错误，此时我们通过Resume Next 来捕捉错这个错误
        ret = ret + 1
        If ErrF Then Exit For
    Next
    ArrayRange = ret
    Exit Function
ErrHandle:
    ret = i
    ErrF = True
    Resume Next
End Function

 

 

 

 测试情况：

1、简单数据的聚类

原始数据为:
1    2   
2    3   
1.5    2.5   
1.5    2   
5.1    1   
4.1    1   
5    3   
6    2   
聚类中心为:
1.500    2.374   
5.062    1.750   
隶属矩阵为:
1.00 1.00 1.00 1.00 0.00 0.03 0.02 0.00
0.00 0.00 0.00 0.00 1.00 0.97 0.98 1.00
迭代次数为:2

以下是一组气候的统计数据，根据要求我们把气候分为三类：

原始数据为:
1    3.5    1    0   
2    2.5    2    2   
2    3.5    1    1   
3    3    3    1   
3    3    1    1   
5    .5    5    2   
6    1.5    4    0   
6    1.5    4    1   
5    3    2    2   
4    3    1    2   
聚类中心为:
4.434    2.992    1.600    1.948   
5.740    1.251    4.250    0.931   
1.902    3.280    1.204    0.845   
隶属矩阵为:
0.09 0.26 0.02 0.40 0.26 0.12 0.08 0.02 0.92 0.88
0.04 0.08 0.00 0.16 0.04 0.82 0.89 0.97 0.04 0.03
0.87 0.67 0.98 0.44 0.70 0.06 0.04 0.01 0.03 0.09
迭代次数为:4
每个样本的类别为：
3 3 3 3 3 2 2 2 1 1

这个分析的结果是可以接受的。

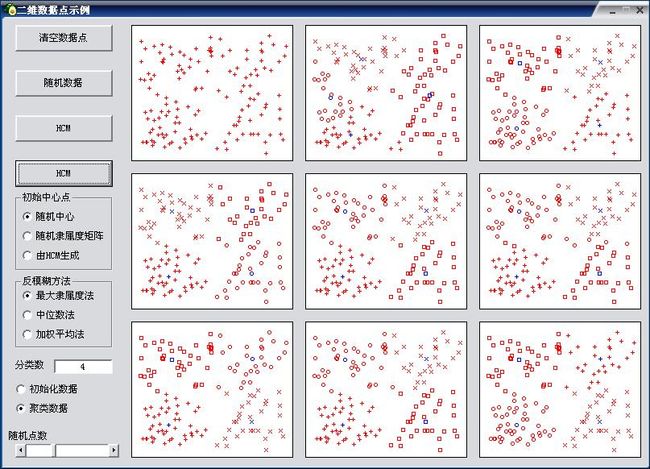
2 、二维数据的聚类

随机生成二维的数据，然后比较分类结果

 

 上图中第一排第二个式HCM的结果，其他的图是不同的参数相结合的FCM的结果，至于结果的好坏对于这些点群不好说。

  这副图选择的聚类类别为4，中间那4个点被聚集到左上角的一类，FCM和HCM的结果是一样的。

      上面这副图的聚类类别为4，但他显示出无论HCM还是FCM都没有给出合理的分类，产生这一现象的原因与其说是算法的问题，不如说是对距离的定义，在FCM/HCM中我们使用的是欧式距离，这使得中间那一部分到左侧的距离要近一些，因此被聚集到这个类中。通过适当改变对距离的定义，我们也可以得到合理的结果。

3 、 图像分割中的应用。

图像分割也是数据聚类的过程，我们选择图像的原始象素矩阵为聚类样本。效果如下：

 

        第一行第二列是HCM的结果，其他是不同参数FCM的结果，其中第四副是采用加权平均反模糊化的，看到这副效果是比较差的，边缘有很多毛刺，这是因为加权平均的过程有个取整的操作所造成的。

      这副图片是在工业现场拍摄的一副火焰图像，我以前做一个项目用到的，分割后的图片根据一定的原理可以得到一定温度 ，并且能大概的不同燃料和其他物份的分布状况。

    在常用的二值化及其vb.net实现一文中，我曾提到用模糊聚类的方法二值化图像，应该说这种方法有其合理之处，他不同于其他的阀值分割，二带有一定模糊信息，并且能方便实现彩色二值分割（即样本的维数为3）。

 

       如上图，程序完美的把天空绿草和树木分开。

      当然FCM在其他方面也有着广泛的应用。

      以上是最基本的模糊聚类算法，针对FCM的计算速度慢的特点，人们提出了快速FCM的步骤，不过那玩意我没看懂是什么意思。 

      前面我说过遗传算法，遗传算法在优化方面有很大的优势，而FCM算法实际上就是找到目标函数的最小值，因此可以把两者结合起来从而获得更好的效果。

 

最后谈一点速度优化方面的问题：

1、FCM算法的计算量是比较大的，在算法模型不变的情况下我们可以通过以下方法减小计算量.   a.如果对某一个特定的问题，我们知道聚类中心的大概位置，则通过程序提供的CreateByHand方法运行。 b、在不确定聚类中心的情况下，选择聚类中心由HCM产生，HCM算法的速度是相当块的。  c.针对不同对象选择不同数据类型，这点在下面要讲到。

2、如果处理对象是图像，则数据量一般很大，速度就是关键了。考虑到图像数据是byte类型的，则可以把FCM算法的Data()参数数据类型改为byte,我们知道浮点数的运算总是很慢的。并且考虑到象素值没有小数部分，程序中有些/可以改为/，整除总比一般除法块，还有既然确定了样本的第二维，则把程序中所有的 DataSize改为3，并且对于所有的有关DataSize的小循环，全部改为手写。

3、实践证明，RndDegree(i, k)^Exponent 的计算速度比 Exp(Log(RndDegree(i, k)) * Exponent)要慢。X^2 比X*X要慢，我是指大数据量的。