图论基础
图概述
图(Graph)是一种比线性结构和树形结构都要复杂的数据结构。简单讲,图是由表示数据元素的的集合V和表示数据之间关系的集合E组成。其中,数据元素常称作顶点(vertex),数据之间的关系常称作边(edge)。故图可记为G=<V,E>,其中V是顶点的有穷非空集合,E是边的集合。在图中顶点的前驱和后继是不设限制的,因此图描述的是一种网状关系。
无向图
若边是无序的或者说是无向的,则称此图是无向图。若无向图中有边(vi,vj)(无向图中边用圆括号表示),则显然(vj,vi)和(vi,vj)是同一条边。
有向图
若边是有序的或者说是有向的,则称此图是有向图。若有向图中有边<vi,vj>(有向图中边用尖括号表示),则显然<vj,vi>和<vi,vj>不是同一条边。有向图中的边也称为弧(arc),对于弧<vi,vj>,vi是弧尾(边的起点),vj是弧头(边的终点)。
示例图
无向图 G1=<V1,E1> V1={v0,v1,v2,v3,v4} E1={(v0,v1),(v0,v2),(v1,v3),(v2,v3),(v2,v4),(v3,v4)}
有向图 G2=<V2,E2> V2={v0,v1,v2,v3} E2={<v0,v1>,<v0,v2>,<v2,v0>,<v2,v3>,<v3,v0>}
图的存储
所谓的图的存储,主要是想从存储结构中表达各顶点之间的联系,也就是表现图中的边。因为顶点总是很好存储的,如最常见的一维数组存储边:
顶点
| v0 | v1 | v2 | v3 | v4 |
或者是
| A | B | C | D | E |
邻接矩阵(adjacency matrix)和邻接表(adjacency list)是图的两种常见存储方式。
如上,无向图G1,对于顶点Vi和顶点Vj,若有边,则(Vi,Vj)=1,否则(Vi,Vj)=0。显然(Vi,Vi)=0,此时的邻接矩阵如下:
| V0 | V1 | V2 | V3 | V4 | |
| V0 | 0 | 1 | 1 | 0 | 0 |
| V1 | 1 | 0 | 0 | 1 | 0 |
| V2 | 1 | 0 | 0 | 1 | 1 |
| V3 | 0 | 1 | 1 | 0 | 1 |
| V4 | 0 | 0 | 1 | 1 | 0 |
显然,由于是无向图,该矩阵是对称的。邻接矩阵所需的存储空间的大小与边数无关,而与顶点数有关。它所需的空间复杂度是O(n^2),n是顶点数。
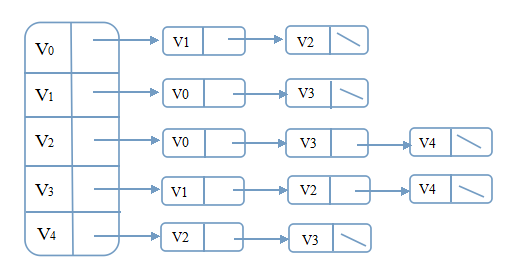
同样的,若是使用邻接表来存储无向图G1,邻接表如下:
邻接表实质就是链式存储。
对于有权图,在邻接矩阵中只需把1改为为相应的权值即可,在邻接表中顶点结构体则需添加成员表示权值。
常用概念
- 顶点的度(degree):与顶点关联的边的数目,记为D(v)。特别的,在有向图中,把顶点v作为终点的弧的数目是入度(in degree),记为ID(v);把顶点v作为起点的弧的数目是出度(out degree),记为OD(v)。显然,D(v)=ID(v)+OD(v)。
- 顶点v1和顶点v2若是有边相连的,则称它们是相邻的(adjacent)。
- 用n表示顶点数,e表示边数。则无向图中e是[0,n(n-2)/2](update:正确的是[0,n(n-1)/2]);有向图中e是[0,n(n-1)]。
- 边数较少的图称为稀疏图(sparse graph),边数较多则称为稠密图(dense graph)。
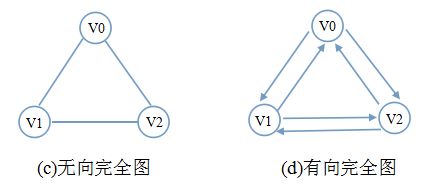
- 完全图:任意两个顶点之间都有边相关联的是完全图。完全图中边数达到最大。细分为无向完全图和有向完全图。
- 有时边是带有权值的,这个权值可以表示从一个顶点到另一个顶点的距离、代价、耗费等。这样的图也称为带权图。
- 子图:设G=<V,E>是一个图,V1是V的子集,E1是E的子集,且E1中的边只与V1中的顶点有关,则称G1=<V1,E1>是G的的子图(subgraph)。
- 路径:在无向图中顶点序列:vi,vj,…,vk,且相邻两顶点之间是有边的,则这个序列构成一条路径。在有向图中,构成路径的不仅是要有边,而且边的方向正确:只能是起点到终点。
- 简单路径:路径中不存在重复顶点,则是简单路径(simple path)。
- 环:在一条路径中,只有第一个顶点和最后一个顶点相同,这条路径就是环(cycle)或回路。
- 路径长度:路径上边的数目。
- 无环图:没有环的图(acyclic graph)。在有向图中,那就是有向无环图。
- 在无向图中,若顶点vi和vj是有路径的,则称vi和vj是连通的(connected)。若图中任意两个顶点都是连通的,则称该图是连通图。
- 连通分量:无向图中的极大连通子图。(所谓的极大是指再加入任意一个顶点,则不连通)
- 在有向图中,任意两个顶点之间都有一条有向的路径,则称该有向图是强连通图。
- 强连通分量:有向强连通的极大子图称为有向图的强连通分量或强连通分支。
转载请注明出处,本文地址:http://blog.csdn.net/zhangxiangdavaid/article/details/37915329
若有所帮助,顶一个哦!
专栏目录:
- 数据结构与算法目录
- c指针