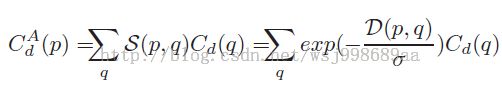Stereo Matching文献笔记之（二）：《A Non-Local Cost Aggregation Method for Stereo Matching》读后感~

最近一直在做stereo matching方向的研究，仔细研读了包括局部算法，全局算法，以及半全局算法三个方面的算法文献，对该方向有了比较清晰的了解，这次分享一下我对杨庆雄的经典文献《A Non-Local Cost Aggregation Method for Stereo Matching》（简称NL算法）的一些理解。

之所以想分享这篇文献，是因为文献明确抛弃了support window的算法思想，指出support window在视察估计上普遍具有陷入局部最优的缺陷，创新性的提出了基于全局最小生成树进行代价聚合的想法，我觉得这个想法非常厉害，全局算法早就有了，但是往往是基于复杂的优化算法，重心放在了视察粗估计和迭代求精两步，十分耗时，而最小生成树，可以天然地建立像素之间的关系，像素之间的关系一目了然，可以大幅减少代价聚合的计算时间，文献表述为线性搜索时间。计算聚合代价的过程不需要迭代，算法时间复杂度小，符合实际应用的需求，所以NL算法已经获得了不错的引用率。在后续算法中得到了很多改进，一些好的立体匹配算法，如CSCA，ST等都是基于NL进行了改进，以下部分着重说说我对NL核心部分，最小生成树(MST)的理解。

(转载请注明：http://blog.csdn.net/wsj998689aa/article/details/45041547, 作者：迷雾forest)

1. 算法思想

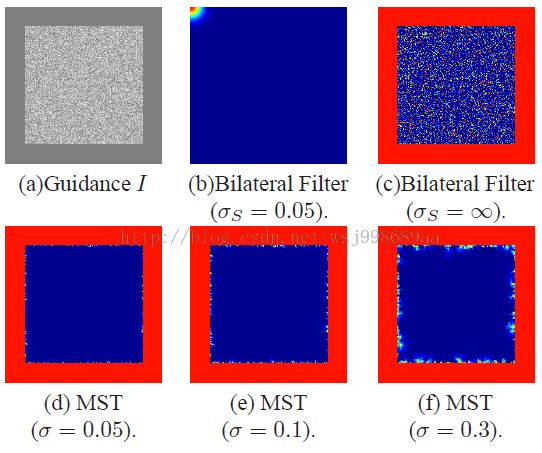
本文的算法思想，是放弃原有的基于支持窗口的方式，采用基于全局MST的方式，构建代价聚合公式。因为支持窗口的办法，本质上只考虑了窗口内像素对中心像素的影响，窗口之外的像素的影响彻底忽略，其实想想看，这样做也没有什么不妥，但是它并不适用一些场合，比如文献列举的图像，

左上角的图像就是原始灰度图像，这个时候我们就会发现，这幅图像中像素与像素之间的关系用支持窗口来处理明显不灵，比如说周围框状区域的任何一个像素，肯定与框状区域内部的像素的深度信息一致，而与中间区域的像素不同。或者说，如果单考虑颜色信息，红框内的像素关系最大，如何表征这样的关系就是一个问题。很遗憾，我们不能事先提取出这样的区域，因为图像分割真的很耗时，并且不稳定，这就是作者的牛逼之处，他想到了MST可以表示这种像素关系，于是采用像素之间颜色信息作为“边权值”，进一步构建MST。

这里还要仔细说一下，这几幅图代表的其实是全图像素点对（0,0）点的权值大小，大家可以看一下论文里面BF的公式，也就是b、c两幅图，文章把参数看成了窗口的大小标志，如果参数足够大，其实exp里面的值就是0，空间信息的作用完全消失，这个时候就要看像素颜色差的作用了，我想这一点给作者一个提示，那就是BF中空间信息的考虑可能是多余的！！！于是作者只利用颜色差信息来构建MST。

MST指的是最小生成数，全称是最小权重生成树。它以全图的像素作为节点，构建过程中不断删除权值较大的边。注意，是全图所有的像素，然后采用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法进行计算。这样便得到了全图像素之间的关系。然后基于这层关系，构建代价聚合，这便是文章标题Non-Local Cost Aggregation的由来。

通过MST计算权值的效果如上图第二行所示，红色代表高权值，蓝色代表低权值。明显发现MST有效的表征了像素对像素的影响。代价聚合公式如下所示，具体的符号含义，这里就不说了，相信做过立体匹配的童鞋一眼就会看明白。

2. 算法核心

我当时看到这里，顿时产生了一个疑问，这样做的代价聚合考虑到的是全部的像素，那么耗时岂不是很惊人？因为我是逐像素计算视差的啊，每个像素都要考虑周围所有的像素。。。。这时间复杂度可能太恐怖点了吧！？果不其然，我自己试了一下这种最粗暴的方式，2分钟都算不完一幅图。

请原谅我的愚钝，作者既然考虑到了MST，说明MST的性质也要被很好的利用，我总结MST在计算效率上的一句话是：MST可以将计算范围从所有节点缩小到父节点和子节点上。因为人家是一棵树嘛！比如说，全图320*240，也就是76800个节点，而父节点只有一个或多个子节点（其实最多只有3个，因为是4邻居），算法效率可想而知。下文就说一下我对算法过程的理解。

2.1 leaf-to-root

假设上图是一个MST，边上的数值代表权重，此时如果计算的是V4的代价聚合，那么很容易，直接计算子节点（V3， V4）的代价聚合值与各自边缘的乘积集合，因为V4是根节点，不需要考虑父节点的影响。公式如下所示，

箭头向上代表从叶子到当前节点的代价聚合值，为何只需要考虑子节点，而不考虑孙子节点，重孙子节点等等的原因就是由于在我们实际计算的时候，要从叶子节点一层一层往上算，这样就会利用树的特性，子节点的代价聚合值已经包含了孙子节点等等对我自己的影响。有点一本万利的感觉。。。

2.2 root-to-leaf

但是这样做是不够的，上面的V4没有父亲节点，属于特殊情况，如果我们要计算V3的代价聚合值呢？显然只考虑V1和V2是不够的，还得考虑V4的影响。也就是从上到下的影响。如图所示：

注意和上一幅图的区别，这个时候我们完全可以假设V3为根节点，它的父节点也变为他的子节点，这样的话，可以利用同样的办法，将V4的代价聚合值乘以它的权重一起再加进来。但是，这里还是有区别的，因为V4的代价聚合值已经考虑到了V3的影响，所以必须事先将V4的代价聚合值减去V3的代价聚合值才可以。公式如下所示：

其中，从上向下的代价聚合值就是最终的代价聚合值，同上一步一样的方式，要从上到下一层一层的计算代价，这样便可节省很多计算量。

2.3 时间复杂度

由于MST的性质，使得原本对全部像素的比较，只需要对父节点，子节点的比较即可，每次计算代价聚合值，从上述公式看来只需要一次加法，一次减法和三次乘法，这样便极大提高了速度，同时又考虑到了全局像素的影响。在middlebury上数据集的平均计算时间仅为90毫秒。

作者提供了文献和源代码的同时，也给出了一个ppt，就在作者的主页上，对其算法原理仍旧迷惑的童鞋可以下载去看看。

3. 实验效果&结论

实验效果就不介绍了，论文上一目了然，这篇文章提供了源码，大家可以跑跑看，我这边针对一般场景进行了测试，效果还是很不错的，经过进一步优化可以进行实际应用。这篇文章比较经典，一些后续的算法就是对其进行了改进，比如说分割树算法《Segment-Tree based Cost Aggregation for Stereo Matching》，将图事先进行区域分割，再在各个区域中计算MST，在生成MST的过程中，考虑到了颜色值与距离作为边缘权值，取得了比NL更好的效果。

4.后记

今天突然看到网上另外一篇关于本文的读后感，发表的时间是在今年的3月份，写的不错，我们二人文章是从不同的角度阐述，附上连接，感兴趣的朋友不妨结合着看一看，作者最后提出了两个代码问题，我认为是这样的：为了避免一棵树出现很长的情况，作者在代码中利用路径压缩的方法连接不同子树，如果两颗子树的高度相同，那么一颗子树的高度只加上1，另外一颗子树的根节点作为子节点；如果二者高度不同，那么一定是高度小的树作为高度大的树的子树，小树的根节点作为大树根节点的子节点，这样合并之后的树的高度就不会变，非常的巧妙。但这些代码细节在论文中是不会被提及的，所以代码非常值得仔细研究评估。

（《 基于MST的立体匹配及相关改进（A Non-Local Cost Aggregation Method for Stereo Matching） 》，http://www.bubuko.com/infodetail-668886.html）