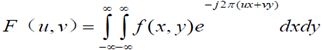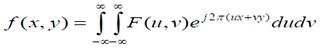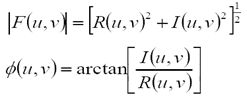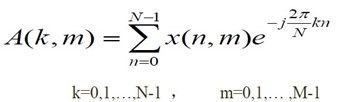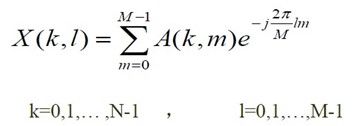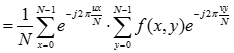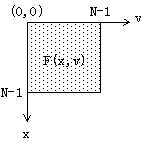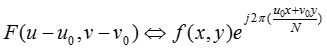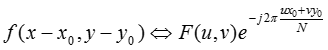傅里叶变换在图像处理中的应用

目录

1.理解二维傅里叶变换的定义    2

1.1二维傅里叶变换    2

1.2二维离散傅里叶变换    2

1.3用FFT计算二维离散傅里叶变换    3

1.3图像傅里叶变换的物理意义    4

2.二维傅里叶变换有哪些性质？    5

2.1二维离散傅里叶变换的性质    5

2.2二维离散傅里叶变换图像性质    6

3.任给一幅图像，对其进行二维傅里叶变换和逆变换    7

4.附录    9

4.1matlab代码    9

4.2参考文献    10

 

1.理解二维傅里叶变换的定义

1.1二维傅里叶变换

二维Fourier变换:

逆变换：

1.2二维离散傅里叶变换

一个图像尺寸为M×N的 函数的离散傅里叶变换由以下等式给出：

其中 和。其中变量u和v用于确定它们的频率，频域系统是由所张成的坐标系，其中和用做（频率）变量。空间域是由f(x,y)所张成的坐标系。可以得到频谱系统在频谱图四角处沿和方向的频谱分量均为0。

离散傅里叶逆变换由下式给出：

令R和I分别表示F的实部和需部，则傅里叶频谱，相位角，功率谱（幅度）定义如下：

1.3用FFT计算二维离散傅里叶变换

二维离散傅里叶变换的定义为：

    

二维离散傅里叶变换可通过两次一维离散傅里叶变换来实现:

1）作一维N点DFT（对每个m做一次，共M次）

2）作M点的DFT（对每个k做一次，共N次）

这两次离散傅里叶变换都可以用快速算法求得,若M和N都是2的幂,则可使用基二FFT算法,所需要乘法次数为                                    

而直接计算二维离散傅里叶变换所需的乘法次数为（M+N）MN，当M和N比较大时用用FFT运算，可节约很多运算量。

1.3图像傅里叶变换的物理意义

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。傅里叶变换在实际中有非常明显的物理意义，设f是一个能量有限的模拟信号，则其傅里叶变换就表示f的频谱。从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数。

傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数傅里叶变换以前，图像（未压缩的位图）是由对在连续空间（现实空间）上的采样得到一系列点的集合，通常用一个二维矩阵表示空间上各点，记为z=f(x,y)。又因空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就必须由梯度来表示，这样我们才能通过观察图像得知物体在三维空间中的对应关系。

傅里叶频谱图上我们看到的明暗不一的亮点，其意义是指图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅里叶变换后的频谱图，也叫功率图，我们就可以直观地看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的、边界分明且边界两边像素差异较大的。

对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外，还有一个好处，它可以分离出有周期性规律的干扰信号，比如正弦干扰。一幅频谱图如果带有正弦干扰，移频到原点上就可以看出，除了中心以外还存在以另一点为中心、对称分布的亮点集合，这个集合就是干扰噪音产生的。这时可以很直观的通过在该位置放置带阻滤波器消除干扰。

2.二维傅里叶变换有哪些性质？

2.1二维离散傅里叶变换的性质

1）分离性

二维离散傅里叶变换具有分离性

 

 

分离性质的主要优点是可借助一系列一维傅里叶变换分两步求得。第1步，沿着的每一行取变换，将其结果乘以1/N,取得二维函数;第2步，沿着的每一列取变换，再将结果乘以1/N,就得到了。这种方法是先行后列。如果采用先列后行的顺序，其结果相同。

如图：

 

 

 

 

 

对逆变换f(x,y)也可以类似地分两步进行。

2）平移性

傅里叶变换和逆变换对的位移性质是指：

 

由乘以指数项并取其乘积的傅立叶变换，使频率平面的原点位移至。同样地，以指数项乘以并取其反变换，将空间域平面的原点位移至当N/2时，指数项为：

即为

这样，用^(x+y)乘以就可以将的傅里叶变换原点移动到N*N频率方阵的中心，这样才能看到整个谱图。另外，对的平移不影响其傅里叶变换的幅值。

此外，与连续二维傅里叶变换一样，二维离散傅里叶变换也具有周期性、共轭对称性、线性、旋转性、相关定理、卷积定理、比例性等性质。这些性质在分析及处理图像时有重要意义。

2.2二维离散傅里叶变换图像性质

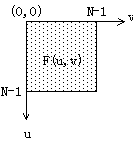
1、图像经过二维傅里叶变换后，其变换系数矩阵具有如下性质：若变换矩阵原点设在中心，其频谱能量集中分布在变换系数短阵的中心附近(图中阴影区)。若所用的二维傅里叶变换矩阵的原点设在左上角，那么图像信号能量将集中在系数矩阵的四个角上。这是由二维傅里叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。

2、图像灰度变化缓慢的区域，对应它变换后的低频分量部分；图像灰度呈阶跃变化的区域，对应变换后的高频分量部分。除颗粒噪音外，图像细节的边缘、轮廓处都是灰度变化突变区域，它们都具有变换后的高频分量特征。

 

3.任给一幅图像，对其进行二维傅里叶变换和逆变换

原图	二维傅里叶变换
逆变换	频谱图

原图	加入高斯躁声	加入椒盐躁声
	对高斯躁声中值滤波	对椒盐躁声中值滤波
	对高斯躁声算术均值滤波	对椒盐躁声算术均值滤波

 

4.附录

4.1matlab代码

1）程序一

[i,lcmp]=imread('F:/123.jpg');%=======读取图像 显示图像

subplot(2,2,1),imshow(i,lcmp);

title('original');

ii=im2double(i); %=====将图像矩阵类型转换为double（图像计算很多是不能用整型的），没有这个会报错！！ ，如果不用这个就必须转化为灰度图！

i1 = fft2(ii); %======傅里叶变换

i2 =fftshift(i1); %======将变换的频率图像四角移动到中心（原来良的部分在四角 现在移动中心，便于后面的处理）

i3=log(abs(i2)); %=====显示中心低频部分，加对数是为了更好的显示

subplot(2,2,2),imshow(i3,[]);

title('Fourier');

map=colormap(lcmp); %===取色谱

imwrite(i3,map,'f:/ffttank.bmp'); %===将上面i3输入到ffttank文件中

i5 = real(ifft2(ifftshift(i2))); %===频域的图反变换到空域 并取实部

i6 = im2uint8(mat2gray(i5)); %===取其灰度图

imwrite(i6,map,'f:/tank2.bmp','bmp'); %===利用灰度图和原来取得颜色模板 还原图像

subplot(2,2,3),imshow(i6);

title('anti-Fourier');

i7=rgb2gray(i);

i8=fft2(i7);%===对灰色图才能归一化。因为那是2维矩阵，彩色图是3维矩阵，需要转化为2维灰图

m=fftshift(i8); %直流分量移到频谱中心

%RR=real(m); %取傅立叶变换的实部

%II=imag(m); %取傅立叶变换的虚部

A=abs(m);%计算频谱幅值

%A=sqrt(RR.^2+II.^2);

A=(A-min(min(A)))/(max(max(A))-min(min(A)))*225; %归一化

subplot(2,2,4),imshow(A); %显示原图像

colorbar; %显示图像的颜色条

title('FFT spectrum'); %图像命名

 

 

2）程序二

m=imread('F:/123.jpg');

M=rgb2gray(m); %==滤波函数都是对二维灰度图，Tif可直接滤波

subplot(3,3,1)

imshow(M);%显示原始图像

title('original')

P1=imnoise(M,'gaussian',0.02); %加入高斯躁声

subplot(3,3,2)

imshow(P1) %加入高斯躁声后显示图像

title('gaussian noise');

P2=imnoise(M,'salt & pepper',0.02); %=加入椒盐躁声

subplot(3,3,3)

imshow(P2) %%加入椒盐躁声后显示图像

title('salt & pepper noise');

g=medfilt2(P1); %对高斯躁声中值滤波

subplot(3,3,5)

imshow(g)

title('medfilter gaussian')

h=medfilt2(P2); %对椒盐躁声中值滤波

subplot(3,3,6)

imshow(h)

title('medfilter salt & pepper noise')

l=[1 1 1 %对高斯躁声算术均值滤波

1 1 1

1 1 1];

l=l/9;

k=conv2(P1,l);

subplot(3,3,8)

imshow(k,[])

title('arithmeticfilter gaussian')

%对椒盐躁声算术均值滤波

d=conv2(P2,l);

subplot(3,3,9)

imshow(d,[])

title('arithmeticfilter salt & pepper noise')

 

4.2参考文献

[1]孟凡文, 吴禄慎.基于FTP的二维傅里叶变换的研究.激光与红外. 第38卷第9期　2008年9月　　　　　　　

[2] 董健，邓国辉，李金武. 基于二维傅里叶变换实现图像变换的研究. 福建电脑. 2015年第 9期