C++卷积神经网络实例：tiny_cnn代码详解（8）——partial_connected_layer层结构类分析（上）

　　在之前的博文中我们已经将顶层的网络结构都介绍完毕，包括卷积层、下采样层、全连接层，在这篇博文中主要有两个任务，一是整体贯通一下卷积神经网络在对图像进行卷积处理的整个流程，二是继续我们的类分析，这次需要进行分析的是卷积层和下采样层的公共基类：partial_connected_layer。

　　一、卷积神经网络的工作流程

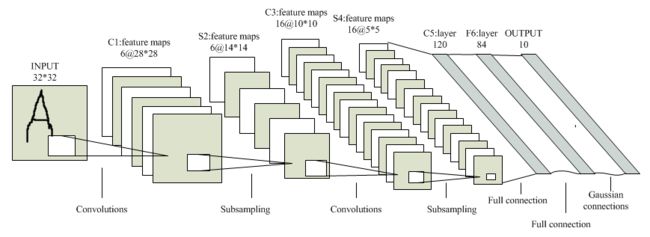
　　首先给出经典的5层模式的卷积神经网络LeNet-5结构模型：

　　这是一个典型的卷积层-下采样层-卷积层-下采样层-卷积层-全连接层模式的CNN结构，接下里观察在我们的程序实例中对网络的初始化情况：

　　（1）卷积层C1：输入图像的尺寸为32*32，卷积核尺寸（卷积窗口尺寸）为5*5，输入数据模板数量为1，卷积核模板种类为6个，导致C1层对每个输入的图像进行卷积操作之后，得到6个卷积特征模板输出，并且卷积后图像的尺寸变为32-5+1=28

　　（2）均值下采样层S2：输入图像的尺寸为28*28，输入数据矩阵的个数为6个，均值下采样是的邻域窗口为2*2,。这里需要强调的一点是S2和C1是相邻层，S2以C1层的输出为输入，因此S2的输入尺寸等于C1的输出尺寸，S2的输入特征模板个数等于C1的输出特征模板个数，并且这两层之间的连接方式为全连接。S2层由于对输入数据矩阵进行了2*2的均值下采样，因此导致数据尺寸会缩小为原来的四分之一，即14*14。

　　（3）卷积层C3：输入图像尺寸为14*14，卷积核尺寸为5*5，输入数据模板数量为6个，该层卷积模板种类为16个，导致C3层对每个输入的图像进行卷积操作之后，得到16个卷积特征模板输出，并且卷积后图像的尺寸变为14-5+1=10。并且C3层与S2层之间的连接属性并非是默认的全连接，而是按照指定连接方式（存储在connection变量中）进行连接。

　　（4）均值下采样层S4：输入数据矩阵的尺寸为10*10，输入数据矩阵的个数为16个，均值下采样的邻域窗口为2*2，与S2相似，这里的下采样操作同样导致矩阵尺寸减半，因此S4层的特征矩阵输入尺寸为5*5。

　　（5）卷积层C5：输入数据矩阵尺寸为5*5，卷积核尺寸为5*5，输入数据模板数量为16，卷积核模板种类为120个。由于在这一层数据矩阵的尺寸已经和卷积核尺寸相同，导致每一次的卷积操作都将得到一个具体数值（即卷积窗口无法进行滑动），导致C5层输出的特征结构是一个120维的特征向量。

　　（6）全连接层：输入特征维数为120，输出特征维数为10（一共有十类），完成特征的分类工作，类此与一个抽象的线性分类函数。

　　（6）激活函数：从代码中可以看出，这里各个层之间的激活函数统一选用tan_h函数，当然tiny_cnn中还封装了很多其他类型的激活函数，在这里可以随便选择，但需要注意的一点是这个网络中理论上只能使用一种类型的激活函数。

　　二、partial_connected_layer类结构

　　在分析partial_connected_layer类的过程中，同样遵循“成员变量-构造函数-功能函数”的分析流程

　　2.1 成员变量

　　partial_connected_layer类主要有以下五个成员变量：

　　这五个成员变量的结构及功能是分析tiny_cnn网络映射机制的一个重点，因此在这里对其着重进行一下分析。首先需要注明一点的是，前三个变量本质上是一个双层vector结构的成员变量，之所以称其为双层vector,是因为在io_connection等别名对应的宏定义中，已经包含了一层vector属性：

　　因此weight2io_、out2wi_、in2wo_、bias2out_均是双层的vector结构，前三个变量的核心存储单元是pair（，），第四个变量的核心存储单元则是一个无符号整型变量，为了更好的说明这种双层vector的特殊结构，这里给出一个示意图：

　　这里之所以采用了双层的vector结构，主要原因在于partial_connected_layer类是一个基类型，需要卷积层和下采样层提供基本层结构框架，而在实际的网络模型中都包含多个相同结构的卷积层和下采样层，在对具体某一层的某一个映射核进行索引时，就需要用到这种双层的vector结构。最外层的vector（vector m）用来标记当前层的具体标号，即指明当前层是具体哪一层；内层的vector（）（vector m1~vector mn）用来索引当前层中具体哪一个卷积核，因为一个卷积核包含多个权重值（例如C1层共有6个卷积核，每个卷积核包含5*5=25个权重值，因此C1层在存储卷积核权重时需要用到6个vecto类型容器，每个容器中包含25个值）。总之一个卷积核中包含多个权重值，一个卷积层中包含多个卷积核，这就要求使用一种双层vector的数据结构对它进行存储，其索引机制一定程度上有些类似于二维数组的索引机制。

　　OK，这篇博客就先介绍到这里，在下一篇博文中我们将着重介绍partial_connected_layer类中的相关构造函数以及一些重要的功能函数。