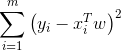简单易学的机器学习算法——线性回归(1)
一、线性回归的概念
对连续型数据做出预测属于回归问题。举个简单的例子:例如我们在知道房屋面积(HouseArea)和卧室的数量(Bedrooms)的情况下要求房屋的价格(Price)。通过一组数据,我们得到了这样的关系:
这样的关系就叫做线性回归方程,其中为回归系数。当我们知道房屋面积以及卧室数量时,就可以求出房屋的价格。当然还有一类是非线性回归。
二、基本线性回归
线性回归的目标是要求出线性回归方程,即求出线性回归方程中的回归系数
。我们可以使用平方误差来求线性回归系数。平方误差可以表示为:
可以使用矩阵表示。对 求导,得到。于是令其为0,即得到
求导,得到。于是令其为0,即得到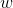 的估计
的估计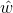
三、基本线性回归实验
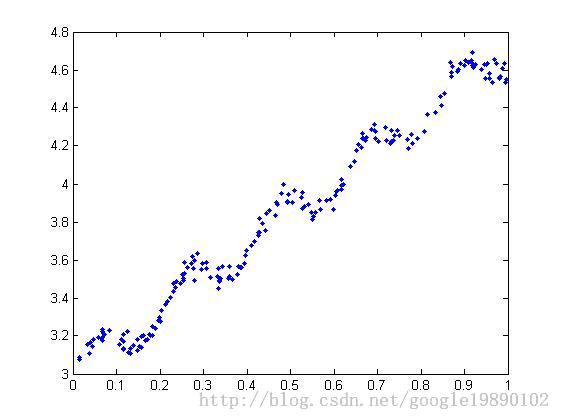
原始的数据
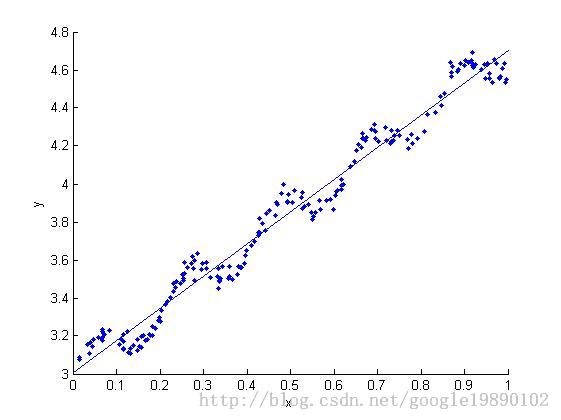
最佳拟合直线
MATLAB代码
主函数
%% load Data
A = load('ex0.txt');
X = A(:,1:2);%读取x
Y = A(:,3);
ws = standRegres(X,Y);
%% plot the regression function
x = 0:1;
y = ws(1,:)+ws(2,:)*x;
hold on
xlabel x;
ylabel y;
plot(X(:,2),Y(:,1),'.');
plot(x,y);
hold off
求权重的过程
function [ ws ] = standRegres( X, Y )
[m,n] = size(X);
ws = zeros(m,1);
XTX = X'*X;
if det(XTX) == 0
disp('This matrix is singular, cannot do inverse');
end
ws = XTX^(-1) *(X'*Y);
end
四、局部加权线性回归
在线性回归中会出现欠拟合的情况,有些方法可以用来解决这样的问题。局部加权线性回归(LWLR)就是这样的一种方法。局部加权线性回归采用的是给预测点附近的每个点赋予一定的权重,此时的回归系数可以表示为
LWLR使用核函数来对附近的点赋予更高的权重,常用的有高斯核,对应的权重为
这样的权重矩阵只含对角元素。
五、局部加权线性回归实验
对上组数据做同样的处理:
MATLAB代码
主函数
%% load Data
A = load('ex0.txt');
X = A(:,1:2);
Y = A(:,3);
[SX,index] = sort(X);%得到排序和索引
%yHat = lwlrTest(SX, X, Y, 1);
%yHat = lwlrTest(SX, X, Y, 0.01);
%yHat = lwlrTest(SX, X, Y, 0.003);
hold on
xlabel x;
ylabel y;
plot(X(:,2),Y(:,1),'.');
plot(SX(:,2),yHat(:,:));
hold off
LWLR
function [ output ] = lwlr( testPoint, X, Y, k )
[m,n] = size(X);%得到数据集的大小
weight = zeros(m,m);
for i = 1:m
diff = testPoint - X(i,:);
weight(i,i) = exp(diff * diff'./(-2*k^2));
end
XTX = X'*(weight * X);
if det(XTX) == 0
disp('his matrix is singular, cannot do inverse');
end
ws = XTX^(-1) * (X' * (weight * Y));
output = testPoint * ws;
end
function [ y ] = lwlrTest( test, X, Y, k )
[m,n] = size(X);
y = zeros(m,1);
for i = 1:m
y(i,:) = lwlr(test(i,:), X, Y, k);
end
end
当
实验数据下载