STL::算法::常见算法
总述
定位
泛型编程(GP)走了一条与面向对象编程(OOP)完全不同的道路,各种容器类的设计与实现也没有走严格意义的继承、接口机制。在STL的设计与实现中,算法并非是容器类的成员函数,而是一种搭配迭代器(架起沟通算法和容器类的桥梁)使用的全局函数。
这样做的一个重要优势在于:所有算法只需实现一份(而不是在每一个容器类的内部都实现一份),就可以对所有容器运作,不必为每一个容器类量身定制。因为算法本身也是模板化的,算法可以操作不同类型之容器内的元素,也可以将之与用户自定义的容器搭配。
算法头文件(header file)
欲使用C++标准库的算法,首先必须包含头文件<algorithm>:
#include <algorithm>某些STL算法用于数值处理,如accumulate,被定义在<numeric>头文件中。
如下代码所示,在使用STL算法时,经常需要用到function object(仿函数对象)或者function adapter,定义在<functional>中。
<algorithm>包含了若干辅助函数:min(), max(), minmax(),这里不妨考察下并不常见的minmax(),
template<typename T>
bool ptr_less(const T* x, const T* y)
{
return *x < *y;
}
template<typename T>
struct lesser :public std::binary_function<T, T, T>
{
bool operator()(const T* x, const T* y)const
{
return *x < *y;
}
}
int main(int, char**)
{
int x = 17, y = 42, z = 33;
int *px = &x, *py = &y, *pz = &z;
std::pair<int*, int*> extremes = std::minmax({px, py, pz}, ptr_less<int>);
// 这里用作比较的function
// 似乎不能进行类型推导,
// 在STL的环境下是不区分function和function object(仿函数)的
//std::pair<int*, int*> extremes = std::minmax({px, py, pz}, lesser<int>());
// function object
cout << *extremes.first << " " << *extrmes.second << endl;
return 0;
}算法重载
STL所提供的各种算法,往往有两个版本(重载),其中一个版本表现为最常用(或最直观)的某种运算,第二个版本表现为最泛化的算法流程,允许用户以template参数来指定所要采行的策略。
下面我们分别以accumulate和sort函数为例:
// version 1
template<typename InputIterator, typename T>
T accumulate(InputIterator first, InputIterator last, T init = T())
// 其实对第三个参数赋初值不仅没有带来形式上的简洁,
// 如果使用默认参数的话,就无法进行参数类型推导
// 反而使形式变得复杂,就这样将就看吧
{
while (first != last)
{
init += *first;
++first;
// init += *first++;
// 虽然这样可能带来形式上的简单,
// 然而后缀++有一个天然的劣势,局部变量的创建
}
return init;
}
// version 2
tempalte<typename InputIterator, typename T, typename BinaryOperation>
T accumulate(InputIterator first, InputIterator last,
BinaryOperation binary_op, T init = T())
{
while (first != last)
{
init = binary_op(init, *first);
++first;
}
return init;
}
int main(int, char**)
{
vector<int> ivec{0, 1, 2, 3, 4, 5};
cout << accumulate<vector<int>::const_iterator, vector<int>::value_type>
(ivec.begin(), ivec.end()) << endl;
return 0;
}算法accumulate用来计算init和[first, last)内所有元素的和。可见出于算法健壮性的考虑,必须提供一个初值init,虽然这个值可能为0,这么做的原因之一是[first, last)区间长度为0(也即first == last)时,仍能返回一个有着明确定义的值。
STL中的算法都是有着严格的规范或者定义的。
accumulate的行为顺序有明确的定义,先将init初始化(传参),然后针对[first, last)区间内的每一个迭代器,依序执行init = init + *i(第一个版本)或init = f(init, *i)(第二个版本)。
我们来实践一下将区间中的每一个元素与init相乘。
template<typename Arg1, typename Arg2, typename Result>
struct binary_function
{
typename Arg1 first_argument_type;
typename Arg2 second_argument_type;
typename Result result_type;
}
template<typename T>
struct multiply :public ::binary_function<T, T, T>
// 使用::域作用符避免与库中的binary_function 相冲突
{
T operator()(const T& x, const T& y) const
// 重载括号运算符,实现对传递进来的两个参数的相乘操作
{
return x * y;
}
}
int main(int, char**)
{
vector<int> ivec {1, 2, 3, 4, 5};
cout << accumulate<vector<int>::const_iterator, vector<int>::value_type>
(ivec.begin(), ivec.end(), mulitply<vector<int>::value_type>(), 1) << endl;
// 1*2*3*4*5 = 120
return 0;
}find 与 find_if
根据equality操作符,循序(++first)查找[first, last)内的所有元素,找出第一个匹配等同(equality)条件者。如果找到,就返回一个InputIterator指向该元素,否则返回迭代器last:
template<typename InputIterator, typename T>
InputIterator find(InputIterator first, InputIterator last,
const T& value)
{
while (first != last && *first != value)
{
++first;
}
return first;
// 如果找到符合条件的值,while退出,返回指向元素的InputIterator
// 如果没有找到,此时first 会遍历到last,
// 并返回最终的last
}我们放宽相等性equality约束,根据指定的pred(predicate:断言)运算条件(function object),循序查找[first, last)内的所有元素,找出第一个满足断言pred者(断言的返回值是bool类型),也就是把pred(*pos)为真者,如果找到就返回一个InputIterator指向该元素,否则返回迭代器last
template<typename InputIterator, typename Predicate>
InputIteraor find_if(InputIterator first, InputIterator last, Predicate pred)
{
while (first != last && !pred(*first))
{
++first;
}
return first;
} 我们以一个找到容器内第一个奇数值为例使用上述的algorithm接口:
template<typename T>
struct is_odd :public unary_function<T, bool>
{
bool operator()(const T& x) const
// 重载括号运算符,即位仿函数
{
return x % 2 != 0;
}
}
int main(int, char**)
{
vector<int> ivec {0, 2, 4, 3, 5};
cout << *::find_if(ivec.begin(), ivec.end(), is_odd<int>()) << endl;
// 使用::域作用符是为了避免与库中的find_if发生混淆。
return 0;
}find_if给我们提供了一种对相等的定义的机会,也就是提供了一种比较的自由,而不是find那样强加的一种对相等的判断,尤其当牵涉到元素不只有一个元素时或者对涉及堆对象的比较时,就只能选择更为灵活的find_if:
class Item
{
private:
std::string _name;
float _price;
public:
Item(const std::string& name, float price):_name(name), _price(price){}
std::string getName() const { return _name;}
float getPrice() const { return _price;}
}
int main(int, char**)
{
vector<Item*> books{new Item("C++", 10.), new Item("Python", 20.), new Item("Machine Learning", 30.)};
// 当然更好的设计是使用shard_ptr智能指针
std::find(books.begin(), books.end(), new Item("C++", 10.));
// 因为是比较的是堆对象,遍历整个序列都不会相等,故find返回的迭代器等于books.end()
std::cout << boolalpha << find(books.begin(), books.end(), new Item("C++", 10.)) == books.end() << std::endl;
// true
// 我们来看find_if的用法
find_if(books.begin(), books.end(), [](Item* book){return book->getName()=="C++"; })
// 使用find_if,也即使用了自定义的相等性定义
// 自然对多属性值进行判断时,可以更加自如地进行判断
return 0;
}transform
在STL的算法(<algorithm>)实现中,一般针对某一函数(也即某一特定算法)都有两个版本(或者叫函数重载),一种是基础版本(表现为最常用或最直观的那种版本),一种是泛化版本。
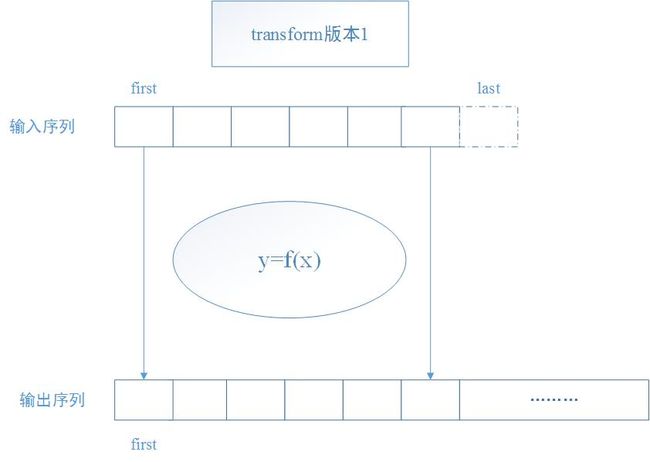
tranform()的第一个版本以一元仿函数op作用于输入序列[first, last)中的每一个元素身上,并以其结果返回一个新序列。第二个版本以二元仿函数binary_op作用于一对元素身上,并以其结果产生一个新序列。如果第二个输入序列的长度小于第一个序列,属于undefined behavior。
关于undefined behavior更详细的讨论请见<矫情的C++——不明确行为(undefined behavior)>。
template<typename InputIterator, typename OutputIterator, typename UnaryOperation>
OutputIterator transform(InputIterator first, InputIterator last,
OutputIterator result, UnaryOperation op)
{
for (; first != last; ++first, ++result)
*result = op(*first); return result; }听其函数名(transform),便可知其极具数学意义。
版本1的数学含义在于:
将输入序列 x 映射为输出序列 y ,当然这一变换(transformation)的性质取决于
UnaryOperation的实现。如
y=x+5 ,表示的就是线性变换(linear transformation)。
template<typename InputIterator, typename OutputIterator, typename BinaryOperation>
OutputIterator transform(InputIterator first1, InputIterator last1,
InputIterator first2, OutputIterator result,
BinaryOperation binary_op)
{
for (; first1 != last1; ++first1, ++first2, ++result)
*result = op(*first1, *first2);
return result;
}版本二的数学含义:
例如本例的: y=x+y ,表示的就是一种二元关系,+是一种二元操作符,即必须有左操作符和右操作符。
客户端代码:
template<typename T>
struct add_five :public std::unary_function < T, T >
{
T operator()(const T& x) const
{
return x + 5; // y=x+5;
}
};
int main(int, char**)
{
std::vector<int> ivec{ 0, 1, 2, 3 };
std::vector<int> ivec2(ivec);
std::vector<int> dst(ivec.size()/*-1*/);
std::vector<int> dst2(ivec.size());
std::transform(ivec.begin(), ivec.end(), dst.begin(), ::add_five<int>());
std::copy(dst.begin(), dst.end(), std::ostream_iterator<int>(std::cout, " "));
std::cout << std::endl;
std::transform(ivec.begin(), ivec.end(), ivec2.begin(), dst2.begin(), ::plus<int>());
std::copy(dst2.begin(), dst2.end(), std::ostream_iterator<int>(std::cout, " "));
std::cout << std::endl;
return 0;
}无论是版本1还是版本,遍历元素时,都是以第一个输入序列为基准的,只要满足第二个输入序列的有效长度不低于第一个输入序列的有效长度,以及输出序列的有效长度不低于输入序列的有效长度即可,自然在函数接口设计时,不需考虑第二个输入学列的尾端迭代器及输出序列的尾端迭代器,只一点由客户端保证。
transform拾遗
transform: y=f(x) ,的本质是建立起一种输入序列和输出序列的映射(map)关系,通过上述代码我们可以发现,除非异常发生,输入和输出的序列长度是一致的,也即输入与输出一一对应,给定一个输入获得一个输出,这不正是函数的定义吗。transform的第二个版本也是如此,只不过从一元函数换成了二元函数 z=f(x,y) 。
transform函数输出区间长度的获得:
// 方式1,预先分配空间
vector<int> v1{...};
vector<int> v2(v1.size());
std::transform(v1.begin(), v1.end(), v2.begin(), func);
// 方式2,使用iterator进行尾插
vector<int> v1{...};
vector<int> v2;
std::transform(v1.begin(), v1.end(), std::back_inserter(v2), func);