UVAlive 3662 Another Minimum Spanning Tree 莫队算法，曼哈顿最小生成树

题目：

现成的东西，就不自己写了。

转载请注明出处，谢谢http://blog.csdn.net/ACM_cxlove?viewmode=contents    by---cxlove

二维平面中有一些点，两点之间的距离为曼哈顿距离，求最小生成树。

朴素的n个点，只能做到O(n^3)或者O(n^2 lgn)。

但是针对这种曼哈顿距离的MST。

其中有个性质是：对于某个点，以他为中心的区域分为8个象限，对于每一个象限，只会取距离最近的一个点连边。

这样的话，由于边是双向的，所以对于每个点只需要考虑4个方向，边的数目最多为O(4*n)，再使用kruskal就可以做到O(nlgn)了。

至于证明：

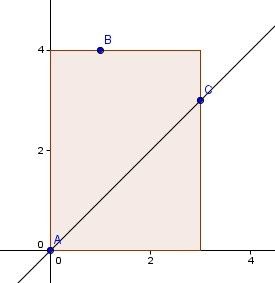
这个结论可以证明如下：假设我们以点A为原点建系，考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2)，不妨设|AB|≤|AC|（这里的距离为曼哈顿距离），如下图：

|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。下面我们分情况讨论：

1.      x1>x2且y1>y2。这与|AB|≤|AC|矛盾；

2.      x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；

3.      x1>x2且y1≤y2。与2同理；

4.      x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。

综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。

转自： http://blog.csdn.net/huzecong/article/details/8576908 

那么如果有了结论之后，怎么样筛选出每个区域最近的点

首先是8个方向，由于边的双向性，我们只需要针对一个点考虑4个方向即可。这4个方向（比如说Y轴右侧），那么都可以通过坐标变换到某一个区域，（比如说y>x）。关于y=x或者y=0对称就可以实现。

对于y>x这个区域，如果对于点A(x0,y0) 在这个区域中有个点B(x1,y1)。

那么x1>x0&&y1-x1>y0-x0。而dist(A,B)=x1-x0+y1-y0=x1+y1-(x0+y0)，那么对于点A，则是找在这个区域内x1+y1最小的点。

那么什么样的点满足在这个区域内呢，（X1>X0&&Y1-X1>Y0-X0）便 是条件

我们将坐标按X排序，将Y-X离散化，用BIT来维护，查询对于某一个X0，查询比(Y0-X0)大的中X1+Y1最小的点。

将这条边加上，重复4个区域之后，就是kruskal了。

我的方法：原理用的是如上的。

实现的时候，也是计算y>x的区域的。但是树状数组以x-y离散化的结果排序的。

因为y'-x' > y-x

所以x'-y' < x-y

其实树状数组不仅可以实现前缀和，也可以实现后缀和，没必要反过来的。但是我就是习惯了

#include<iostream>
#include<cstring>
#include<cstdio>
#include<math.h>
#include<algorithm>
#include<vector>
using namespace std;
#define maxn 100007
#define inf 100000000
#define maxm 200007
#define ll long long
int pos[maxm],tree[maxm];
void add(int p,int val,int id){
    while(p < maxm){
        if(val < tree[p]){
            tree[p] = val;
            pos[p] = id;
        }
        p += p&(-p);
    }
}
int query(int p){
    int id=-1,val=inf;
    while(p > 0){
        if(tree[p] < val){
            val = tree[p];
            id = pos[p];
        }
        p -= p&(-p);
    }
    return id;
}

struct Node{
    int x,y,id,xsy;
};
int comp(Node a,Node b){
    if(a.x == b.x) return a.y > b.y;
    return a.x > b.x;
}
int compxsy(Node a,Node b){
    return a.xsy < b.xsy;
}
struct Edge{
    int u,v,w;
    Edge(int _u=0,int _v=0,int _w=0){
        u =_u,v=_v,w=_w;
    }
};
vector<Edge> edge;
Node point[maxn];
Node P[maxn];
int dist(Node a,Node b){
    return abs(a.x-b.x)+abs(a.y-b.y);
}
void ManhaTon(int n){
    for(int i = 0;i < n; i++)
        point[i].xsy = point[i].x-point[i].y;
    sort(point,point+n,compxsy);
    int cnt = 1,f=-inf;
    for(int i = 0;i < n; i++){
        if(point[i].xsy != f){
            cnt++;
            f = point[i].xsy;
        }
        point[i].xsy = cnt;
    }
    sort(point,point+n,comp);

    for(int i = 0;i < maxm; i++)
        tree[i] = inf,pos[i]=-1;
    for(int i = 0;i < n; i++){
        int u = point[i].id;
        int v = query(point[i].xsy);
        if(v != -1)
            edge.push_back(Edge(u,v,dist(P[u],P[v])));
        add(point[i].xsy,point[i].x+point[i].y,u);
    }
}


void buildEdge(int n){
    edge.clear();
    for(int j = 0;j < 4; j++){
        for(int i = 0;i < n; i++)
            point[i] = P[i];
        for(int i = 0;i < n; i++){
            if(j == 1) swap(point[i].x,point[i].y);
            else if(j == 2)
                point[i].y = -point[i].y;
            else if(j==3){
                swap(point[i].x,point[i].y);
                point[i].y = -point[i].y;
            }
        }
        ManhaTon(n);
    }
}
int pre[maxn];
int find(int u){
    if(u == pre[u]) return u;
    return pre[u] = find(pre[u]);
}
int compEdge(Edge a,Edge b){
    return a.w < b.w;
}
ll MST(int n){
    for(int i = 0;i < n; i++)
        pre[i] = i;
    sort(edge.begin(),edge.end(),compEdge);
    ll d = 0;
    for(int i = 0;i < edge.size() ;i++){
        if(n == 1) return d;
        int f1 = find(edge[i].u);
        int f2 = find(edge[i].v);
        if(f1 == f2) continue;
        pre[f1] = f2;
        n--;
        d+=edge[i].w;
    }
    return d;
}

int main(){
    int n,tt=1;
    while(scanf("%d",&n),n){
        for(int i = 0;i < n; i++){
            scanf("%d%d",&P[i].x,&P[i].y);
            P[i].id = i;
        }
        buildEdge(n);
        printf("Case %d: Total Weight = %lld\n",tt++,MST(n));
    }
    return 0;
}