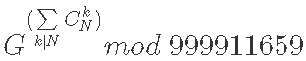BZOJ 1951 SDOI2010 古代猪文 数论 Lucas定理

题目大意：给定N,G,求

首先由欧拉定理易知当A与p互质时A^B %p=A^(B%φ(p) ) %p

这里p是一个质数 于是φ(p)=p-1=999911658

然后由于这个数不是质数 难以处理 我们将它分解质因数 然后对于每个质因数的解用中国剩余定理合并即可

然后就是999911658有一个很好的性质 999911658=2*3*4679*35617 每个质因数的次数都是1次

于是我们可以套用卢卡斯定理 预先处理出对于每个质因数的阶乘和阶乘的逆元即可

注意此题有个细节 就是欧拉定理中a与p必须互质 而当a=0(即G=p)时gcd(a,p)=p

所以有一组数据是专门卡这个地方的 这组数据是999911657 999911659 取模后是0^0 于是得到1 但是答案是0 

于是我们做一些处理 A^B %p=A^(B%φ(p)+φ(p) ) %p

这样就没问题了

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Mo 999911659
#define Phi_Mo 999911658
using namespace std;
typedef long long ll;
typedef pair<ll,ll> abcd;
ll prime[4]={2,3,4679,35617};
ll n,g,ans[5];
ll factorial[4][35617],inverse[4][35617];
void Linear_Shaker(ll p,ll fac[],ll inv[])
{
	ll i;
	fac[0]=1;
	for(i=1;i<p;i++)
		fac[i]=fac[i-1]*i%p;
	inv[1]=1;
	for(i=2;i<p;i++)
		inv[i]=(p-p/i)*inv[p%i]%p;
	inv[0]=1;
	for(i=1;i<=p;i++)
		inv[i]=inv[i]*inv[i-1]%p;
}
ll C(ll n,ll m,ll p,ll fac[],ll inv[])
{
	if(n<m) return 0;
	if(n<p&&m<p)
		return fac[n]*inv[m]%p*inv[n-m]%p;
	return C(n%p,m%p,p,fac,inv)*C(n/p,m/p,p,fac,inv)%p;
}
inline void Calculate(ll x)
{
	int i;
	for(i=0;i<4;i++)
	{
		ans[i]+=C(n,x,prime[i],factorial[i],inverse[i]);
		ans[i]%=prime[i];
	}
}
abcd EXGCD(ll x,ll y)
{
	if(!y) return abcd(1,0);
	abcd temp=EXGCD(y,x%y);
	return abcd(temp.second,temp.first-x/y*temp.second);
}
ll Chinese_Remainder_Theorem()
{
	int i;
	ll re=0;
	for(i=0;i<4;i++)
	{
		abcd temp=EXGCD( Phi_Mo/prime[i] , prime[i] );
		ll x=(temp.first%Phi_Mo*(Phi_Mo/prime[i])%Phi_Mo+Phi_Mo)%Phi_Mo;
		re+=x*ans[i]%Phi_Mo;
		re%=Phi_Mo;
	}
	return re;
}
ll Quick_Power(ll x,ll y)
{
	ll re=1;
	while(y)
	{
		if(y&1)re*=x,re%=Mo;
		x*=x,x%=Mo;
		y>>=1;
	}
	return re;
}
int main()
{

	//freopen("1951.in","r",stdin);
	//freopen("1951.out","w",stdout);

	ll i;
	for(i=0;i<4;i++)
		Linear_Shaker(prime[i],factorial[i],inverse[i]);
	cin>>n>>g;
	for(i=1;i*i<n;i++)
		if(n%i==0)
			Calculate(i),Calculate(n/i);
	if(i*i==n)
		Calculate(i);
	ans[4]=Chinese_Remainder_Theorem();
	ans[4]=Quick_Power(g%Mo,ans[4]+Phi_Mo);
	cout<<ans[4]<<endl;
}