leetcode: Container With Most Water

问题描述：

Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container.

原问题链接： https://leetcode.com/problems/container-with-most-water/

 

问题分析

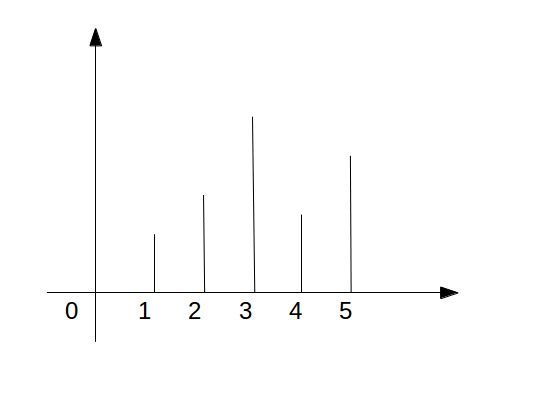
    这个问题的题意一开始有点不太好理解。它的意思是给定一个数组int[]height，它的每个元素的下标对应一个二维坐标的x轴的值，比如里面元素的索引0, 1, 2则对应x轴的值0, 1, 2。它每个下标索引对应的值为对应y轴的值。比如给定一个数组int[]height = { 1, 2, 3} 。那么它们就形成了一组点(0, 1), (1, 2), (2, 3)。这些点向x轴画垂直线的话，则形成对应的一条条的线段。比如从(0, 1)-> (0, 0), (1, 2)-> (1, 0), (2, 3) -> (2, 0)。这样，给定一组这样的数字，它们就形成了一个如下的图形：

 

    现在对于任意两条垂直线段来说，它们加上x轴就构成了一个类似于容器的结构。我们需要找到两个垂直线段，使得它们构成的容器的面积是最大的。

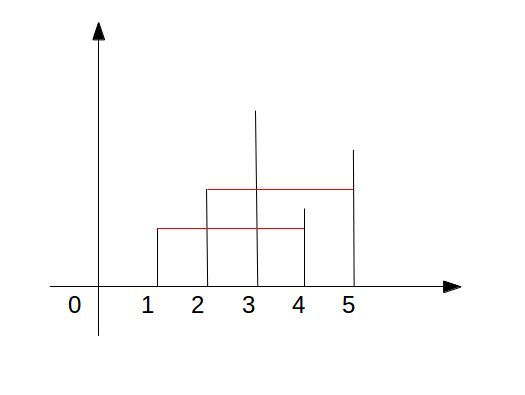
    按照前面问题的要求，我们给定的两条不同的线段就可以构成一个容器。因为要使得这个容器能够装最多的水，那么对应于这两个线段的x轴值之间的差则表示容器的长度。而容器的高度则是取这两个线段中对应y轴值较小的那个。比如下图中我们取x轴为1和4的线段，它们构成了一个容器，而且取2和5这两条线段它们也构成了一个容器。所以现在就是要在这些所有可能构成容器的组合里找到容积最大的那个。

     现在，给定数组中下标为i, j(i < j)的两个元素，它们构成的容器面积则为(j - i) * Math.min(height[i], height[j])。解决了这个基本的问题，我们来看怎么寻找到容积最大的那个容器。

 

方法一

    差不多一开始大多数人都能想到这么一个方法，这个问题的本质在于针对数组里索引不同的两个元素，求它们之间构成的容器，然后再把最大的那个给求出来。因此只要通过一个二重循环找到所有的情况就可以了。这种方法的实现如下：

 

public class Solution {
    public int maxArea(int[] height) {
	int max = 0, len = height.length;
	for(int i = 0; i < len - 1; i++) {
	    for(int j = i + 1; j < len; j++) {
		max = Math.max(max, (j - i) * Math.min(height[i], height[j]));
	    }
	}

	return max;
    }
}

    这种方式比较简单，两重循环，把所有可能性都计算出来比较。方法的时间复杂度为O(N * N) 。总的来说，方法的效率不是很高。那么有没有什么效率更高的方法呢？

 

方法二

    前面的解法是搜索所有可能的情况再来过滤最大值，这样速度就慢了。实际上这里还是有一些规律可以遵循利用的。假设我们最终找到的最大的容器的两个元素的索引为i, j且i < j，那么它们必然满足0 <= i < j <= height.length - 1。这样，它们必然是在0 到height.length -1之间。

    另外，它们要构成一个最大的容积，必然是它们的长和高的乘积是最大的。对于在数组里最两边的两个元素，它们的长肯定是最长的。这个时候如果有一些其他容积比它们要大的肯定是高比它们要大。

    如果我们以数组的两头作为最开始的比较起点。然后从两头向中间推进，该怎么来做选择呢？假设当前左右两个索引点在i, j。如果height[i] < height[j]，那么这个时候构成的容器的高度是height[i]，否则就是height[j]。这个时候如果我们希望能找到可能更大的容器，可以从i这个点向后查找。在满足i < j的情况下，只要我们能找到height[k] > height[i]的节点，这样才可能找到更大的容器。这种情况下为什么不是从右向左呢？因为既然是height[i] < height[j]，它的容器的瓶颈就受制于height[i]，如果此时从右向左移动的话，就算后面的height[j - 1] > height[j]，但是它最高也就是height[i]了，而且向左移动之后它们的长度更加短了，也就是说这种情况根本就不可能有大于原有容器的存在。所以在height[i] < height[j]的时候需要从左往右去移动来排除以i为左边的情况。

    同样，当height[i] > height[j]的情况，则需要从右向左移动。另外，如果height[i] == height[j]呢？这种情况就无所谓了。从左到右或者从右到左都可以了。所以上述的讨论找到的规律概括起来就是当height[i] < height[j]的时候就从左向右遍历去找一个比height[i]大的元素作为下一个候选，当height[i] > height[j]的时候就从右向左的去找比height[j]大的候选。按照这种思路，可以得到如下的代码：

 

public class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1, max = 0;
        while(l < r) {
            int lMax = height[l], rMax = height[r];
            max = Math.max(max, (r - l) * Math.min(lMax, rMax));
            if(height[l] <= height[r])
                while(l < r && height[l] <= lMax) l++;
            else
                while(l < r && height[r] <= rMax) r--;
        }
        
        return max;
    }
}

    这种方法的时间复杂度只有O(N)。它的好处就是只需要比较一下高度就可以里，避免了很多的计算浪费。

 

 

总结

    针对这个求最大容器容积的问题，寻找比较的两个点并利用高度的差别来排除一些点的方法能够大幅的提升性能。当然，这种方法的规律需要认真的分析。