简单易懂的Dancing links讲解(1)
最早接触Dancing Links的时候,是在csdn论坛上逛的时候,发现有人在研究数独程序,由于本人开发过数独游戏,就进去看了看,发现有人说用Dancing Links来求解数独最快了,于是我就决定去了解一下Dancing Links。
1. Dancing Links是什么?
Dancing Links是一类搜索问题的通用优化,对精确覆盖问题有奇效,也可解决重复覆盖问题,DancingLinks的发明者是DonKnuth(《计算机程序设计艺术》的作者)
2. 用途
解决精确覆盖问题。对于接下来的非确定性算法,由于我们没有想到更好的名字,我们将称之为X算法,它能够找到由特定的01矩阵A定义的精确覆盖问题的所有解。X算法是实现试验——错误这一显而易见的方法的一段简单的语句(确实,一般来说,我想不到别的合理的方法来完成这个工作)。
如果A是空的,问题解决;成功终止。
否则,选择一个列c(确定的是选含1最少的列)。
选择一个行r,满足 A[r,c]=1 (不确定的是哪一行)。
把r包含进部分解。
对于所有满足 A[r,j]=1 的j,
从矩阵A中删除第j列;
对于所有满足 A[i,j]=1 的,
从矩阵A中删除第i行。
在不断减少的矩阵A上递归地重复上述算法。
3. 舞蹈步骤
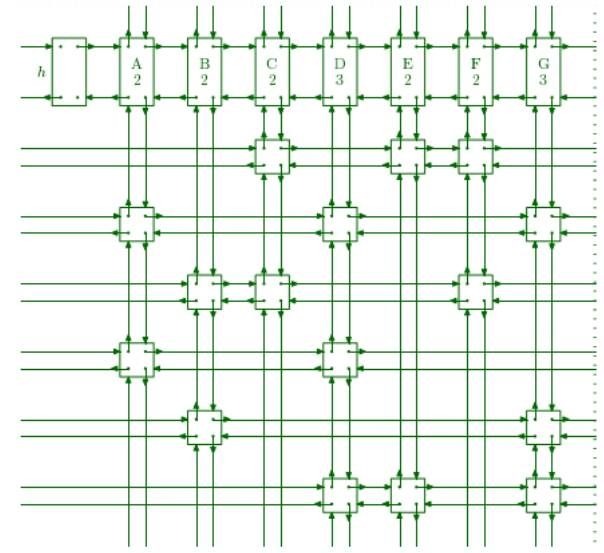
一个实现X算法的好方法就是将矩阵A中的每个1用一个有5个域L[x]、R[x]、U[x]、D[x]、C[x]的数据对象(dataobject)x来表示。矩阵的每行都是一个经由域L和R(左和右)双向连接的环状链表;矩阵的每列是一个经由域U和D(上和下)双向连接的环状链表。每个列链表还包含一个特殊的数据对象,称作它的表头(list header)。
这些表头是一个称作列对象(columnobject)的大型对象的一部分。每个列对象y包含一个普通数据对象的5个域L[y]、R[y]、U[y]、D[y]和C[y],外加两个域S[y](大小)和N[y](名字);这里大小是一个列中1的个数,而名字则是用来标识输出答案的符号。每个数据对象的C域指向相应列头的列对象。
表头的L和R连接着所有需要被覆盖的列。这个环状链表也包含一个特殊的列对象称作根,h,它相当于所有活动表头的主人。而且它不需要U[h]、D[h]、C[h]、S[h]和N[h]这几个域。
我们寻找所有精确覆盖的不确定性算法现在可以定型为下面这个明析、确定的形式,即一个递归过程search(k),它一开始被调用时k=0:
如果 R[h]=h ,打印当前的解(见下)并且返回
否则选择一个列对象c(见下)。
覆盖列c(见下)。
对于每个r←D[c],D[D[c]],……,当 r!=c,
设置 Ok<-r;
对于每个j←R[r],R[R[r]],……,当 j!=r,
覆盖列j(见下);
search(k+1);
设置 r←Ok 且 c←C[r];
对于每个j←L[r],L[L[r]],……,当 j!=r,
取消列j的覆盖(见下)。
取消列c的覆盖(见下)并且返回。
为了选择一个列对象c,我们可以简单地设置c<-R[h];这是最左边没有覆盖的列。或者如果我们希望使分支因数达到最小,我们可以设置s<-无穷大,那么接下来:
对于每个j←R[h],R[R[h]],……,当 j!=h,
如果 S[j]<s 设置 c←j 且 s←S[h]。
那么c就是包含1的序数最小的列(如果不用这种方法减少分支的话,S域就没什么用了)。
覆盖列c的操作则更加有趣:把c从表头删除并且从其他列链表中去除c链表的所有行。
设置 L[R[c]]←L[c] 且 R[L[c]]←R[c]。
对于每个i←D[c],D[D[c]],……,当 i!=c,
对于每个j←R[i],R[R{i]],……,当 j!=i,
设置 U[D[j]]←U[j],D[U[j]]←D[j],
并且设置 S[C[j]]←S[C[j]]-1。
操作(1),就是我在本文一开始提到的,在这里他被用来除去水平、竖直方向上的数据对象。
最后,我们到达了整个算法的尖端,即还原给定的列c的操作。这里就是链表舞蹈的过程:
对于每个i←U[c],U[U[c]],……,当 j!=i,
对于每个j←L[i],L[L[i]],……,当 j!=i,
设置 S[C[j]]←S[C[j]]+1,
并且设置 U[D[j]]←j,D[U[j]]←j。
设置 L[R[c]]←c 且 R[L[c]]←c。
注意到还原操作正好与覆盖操作执行的顺序相反,我们利用操作(2)来取消操作(1)。(其实没必要严格限制“后执行的先取消”,由于j可以以任何顺序穿过第i行;但是从下往上取消对行的移除操作是非常重要的,因为我们是从上往下把这些行移除的。相似的,对于第r行从右往左取消列的移除操作也是十分重要的,因为我们是从左往右覆盖的。)
以上部分,可能太过专业,太抽象,你可能也看不明白,反正我就是一直没弄明白过上面的描述,但是后面会有我自己通过分析程序代码给出的示意图,详细描述了舞蹈的过程,非常直观易懂,所以不懂上面的可直接跳过,不必纠结。
4. Dancing Links的具体实现方法
Dancing Links这种数据结构的实现方法有两种,一个是用双向十字链表来实现,这种方法比较容易理解,另一个是用几个数组来实现,这种方法较另类,较难理解
双向十字链表实现
L[x]和R[x]分别表示x的前驱节点和后继节点。每个程序员都知道如下操作:
L[R[x]] ← L[x],R[L[x]] ← R[x] (1)
是将x从链表删除的操作;但是只有少数程序员意识到如下操作
L[R[x]] ← x,R[L[x]] ← x (2)
dancingLinks的精髓就体现在第二个公式,因为它很方便很高效的实现了链表的恢复图1:dancingLinks的链表结构示意图
dancing links的数组实现
其实是用数组来模拟双向十字链表结构,为方便理解,直接举个例子。
对于如下的01矩阵:1 1 0 0
0 0 0 1
0 1 1 1
1 0 1 0
我们把它的dancinglinks结构描述到如下4个数组中:(Up,Down,Left,Right)
如下:
为什么这4个数组的长度都是13呢?
因为上面的01矩阵有4个列,8个1,我们把头节点head编号为0。列分别编号为1,2,3,4。第一行的两个1编号为5,6,第二行的一个1编号为7,第三行三个1编号为8,9,10。第四行两个1,编号为11,12。编号的顺序都是从左到右。
这样一来,1列的下一个节点就是编号为5的1,编号为5的1的下面又是编号11的1,编号为5的1的左边和右边都是编号为6的1
为便于理解,可以结合图1来看 Remove(5) L[R[1]]=L[1]; R[L[1]]=R[1]; L[R[11]]=L[11]; R[L[11]]=R[11];
Remove(6) L[R[8]]=L[8]; R[L[8]]=R[8]; L[R[2]]=L[2]; R[L[2]]=R[2];

Resume(5) L[R[1]]=R[L[1]]=1 L[R[11]]=R[L[11]]=11
Resume(6) L[R[2]]=R[L[2]]=2 L[R[8]]=R[L[8]]=8
可见数组是可以用来表示双向十字链表结构的