中点Bresenham算法光栅化画直线（个人总结精简版）代码超短！速度极快！

中点Bresenham算法光栅化画直线，每次只位移一个像素，精度高！此源码借助直线 y=x 做了一些转换，简化了主位移的处理，每次移动只需要 加减操作， 不需要乘除！速度极快！！ 原理在最后，下面先贴上核心代码~

void Bresenham_LineTo(CDC *pDC, int x1, int y1, int x2, int y2) //中点Bresenham算法
{
	float k = 1.0*(y2 - y1) / (x2 - x1); //斜率
	int flag = 0;  //是否沿y = x 翻转
	if (k > 1 || k < -1)
	{
		flag = 1;
		x1 ^= y1 ^= x1 ^= y1;
		x2 ^= y2 ^= x2 ^= y2;
		k = 1.0*(y2 - y1) / (x2 - x1);
	}
	float d = 0.5 - k; //初始值
	if (x1 > x2)
	{
		x1 ^= x2 ^= x1 ^= x2;
		y1 ^= y2 ^= y1 ^= y2;
	}
	while (x1 != x2)//主位移，每次都像素+1
	{
		if (k > 0 && d < 0)  //正向
				++y1, ++d;
		else if (k < 0 && d > 0)//负向
				--y1, --d;
		d -= k;
		++x1;
		if (flag) pDC->SetPixel(y1, x1, RGB(255, 0, 0)); //翻转像素点
		else pDC->SetPixel(x1, y1, RGB(255, 0, 0)); 
	}
}

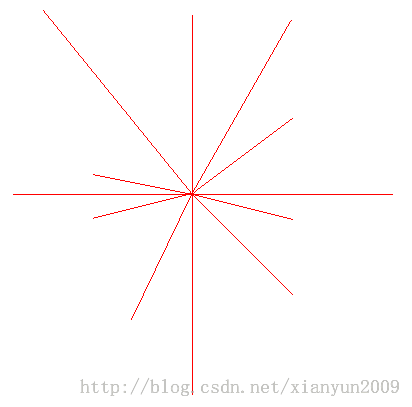
效果图：

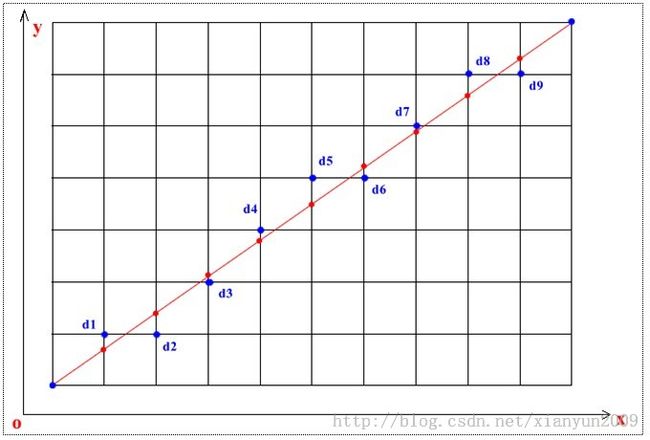
原理：

用蓝色像素点代替红色直线

每次在主位移（宽高中较长的为主位移）移动一个像素，另一个方向走不走取决于中点偏差判别式的值

中点偏差判别式

f(x,y) = y - kx - b = 0 其中 k = (y2-y1)/(x2-x1)

根据f(x,y)的值与0 的关系（ < 0 , = 0 , > 0）判定中点与直线的位置关系

例如.主位移为x， 0 < k < 1 时，按a(x+1, y),b(x+1,y+1)中点与直线比较,然后进行相应处理

a(x+1, y),b(x+1,y+1) 的中点带入偏差判别式可得  d = f(x+1, y + 0.5) = y + 0.5 -  k*(x+1) - b

若d < 0 中点在直线下方，下个像素点画在b，   下一步的d 值为 d = f(x + 2, y + 1.5) = y + 0.5 - k(x+1) - b + 1 - k = d + 1 - k

若d >= 0 中点在直线上方，下个像素点画在a， 下一步的d值为  d = f(x + 2, y + 0.5) = y + 0.5 - k(x+1) - b - k = d - k

过程中的每个d 都可以由上一步通过加减操作得出，操作快速！

d的初始值为 d = f(x + 1, y + 0.5) = y + 0.5 - k(x+1) - b = y - kx - b -k + 0.5

其中(x,y)为起始点，在直线y - kx - b = 0上代入得 d = 0.5 - k