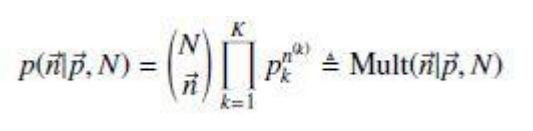LDA理解以及源码分析（一）

LDA系列的讲解分多个博文给出，主要大纲如下：

• LDA相关的基础知识
  
  • 什么是共轭
  • multinomial分布
  • Dirichlet分布
• LDA in text
  
  • LAD的概率图模型
  • LDA的参数推导
  • 伪代码
• GibbsLDA++-0.2源码分析
• Python实现GibbsLDA
• 参考资料

LDA相关的基础知识

LDA是Blei于2002年发表的概率语言模型，被广泛应用于主题建模中，通过对文本进行潜语义分析，发现文本在主题上的概率。通俗点说，给定一堆文档集合documents，每篇document由多个word表示，则LDA的作用就是找到document在topic上的分布情况，以及word在topic上的分布情况，而这些分布都服从某种概率分布，这样，可以解决一词多义这种情况，比如说apple这个词，在“电子产品”和“水果”这两个主题上都有概率，而且可能差不多。

首先，我们先来了解几个知识。

什么是共轭

以二维情况下为例，二项分布的参数p选取的先验分布是Beta分布时，以p为参数的二项分布用贝叶斯估计后得到的仍是Beta分布，所以二项分布和Beta分布共轭。

先验 + 数据的知识 = 后验

① p的先验：f(p)~Beta(p|α,β)
② 数据的知识：例如抛硬币，m次正面，n次负面，m~B(m+n,p)
③ p的后验：f(p|m,n)~Beta(p|α+m,β+n)

Note

• Dirichlet分布是Multinomial分布的先验分布
• 文本模型中，document-topic和topic-word都服从Multinomial分布，其先验选取Dirichlet分布

Multinomial分布和Dirichlet分布

Multinomial分布的分布律如下：

其中，k表示K种实验结果，向量n表示实际的实验结果，向量p表示每种结果发生的概率。

参数p服从参数为α的Dirichlet分布（先验分布），所以α也叫做“超参数”，通常根据经验事先给出。

Dirichlet分布的一个重要性质是参数p上的积分为1，由此可以得到：

这个delta公式会在后面用于LDA的inference。

Dirichlet分布的分布律如下：

Dirichlet的期望为：

LDA in Text

LDA在主题建模中的应用，需要知道以下几点：

• 文档集中的words不考虑顺序，符合Bag Of Word词袋模型，假设总词汇数为V。
• 每篇由n个word生成的document，每个word的生成都服从multinomial分布，就像上帝抛一个有V面的筛子（每面对应一个word），抛n次就可以生成一篇document了。
• document与document之间的筛子不是同一个，每次为document选一个topic筛子，这个过程也服从multinomial分布。

一个通俗的例子如下：

“我们可以假想有一位大作家，比如莫言，他现在要写m篇文章，一共涉及了K个Topic，每个Topic下的词分布为一个从参数为β的Dirichlet先验分布中采样出的Multinomial分布（注意词典由term构成，每篇文章由word构成，前者不能重复，后者可以重复）。对于每篇文章，他首先会从一个泊松分布中采样出一个值作为文章长度，再从一个参数为α的Dirichlet先验分布中采样出一个Multinomial分布作为该文章里面出现每个Topic下词的概率；当他想写某篇文章中的第n个词的时候，首先从该文章中出现每个Topic下词的Multinomial分布中采样一个Topic，然后再在这个Topic对应的词的Multinomial分布中采样一个词作为他要写的词。不断重复这个随机生成过程，直到他把m篇文章全部写完。”

LDA的概率图模型

LDA的概率图如下：

概率图模型分为两个阶段：

（1）α -> θm -> Zm,n ：选取一个参数为θm的doc-topic分布，然后对第m篇文章的第n个词的topic，生成Zm,n的编号。

（2）β -> ψk -> Wm,n|k=Zm,n ：生成第m篇文章的第n个词。

由概率图可以看出，一篇文章m的生成过程为：

1、从一个参数为α的Dirichlet分布中采样出一个multinomial分布θm，作为该文章在k个主题上的分布

2、对该文章里的每个词n，根据上步中的θm分布，采样出一个topic编号来，然后根据此topic-word对应的参数为ψ的多项分布，采样出一个词。

LDA的参数推导

从上面的过程可知，参数α和β是由经验给出，Zmn，θm，ψk是隐含变量，需要推导。LDA的推导方法有两种，一种是精确推导，例如Blei在论文里阐述用EM计算，另一种是近似推导，实际工程中通常用这种方法，其中最简单的是Gibbs采样法。

Gibbs Sampling：是MCMC的一种，其主要思想就是每次迭代只改变一个维度的值，直到收敛输出待估计的参数。用在LDA中时，维度就是词汇集，每次迭代时，根据其他词的主题分配来估计当前词的主题概率。

由LDA的概率图模型可以看出，LDA的联合分布：

前面我们提到过一个delta公式，正是用在了这里。

Gibbs采样推导参数，即排除当前词的主题分配，根据其他词的主题分配和观察到的单词来计算当前词主题的概率公式：

当Gibbs sampling收敛后，我们需要根据最后文档集中所有单词的主题分配来计算θm和ψk。document-topic后验分布和topic-word后验分布分别为：

根据Dirichlet分布的期望公式可以得到：

伪代码

输入：词向量w，超参数α和β，主题数K

全局变量：

• n(m,k) ： 文章m对主题k下的词汇数量
• n(k,t) : 词汇t属于主题k的个数
• n(m) ： 文章m的词汇总数
• n(k) ： 主题k的词汇总数
• p ： 采样的条件变量向量

输出：主题分布向量Z，multinomial分布的参数θ和ψ

伪代码如下：

//初始化
n(m,k) = 0; n(k,t) = 0; n(m) = 0; n(k) = 0;
for all document m do:
    for all words n in document m do:
        sample topic index z(m,n) = k ~ Mult(1/K)
        n(m,k) += 1;  n(k,n) += 1; n(m) += 1; n(k) += 1;
//Gibbs采样
while not finished do:
    for all document m do:
        for all words n in document m do:
            n(m,k) -= 1; n(k,n) -= 1; n(m) -= 1; n(k) -= 1;
            sample topic index k~p(z|z(not n), w);
            n(m,k) += 1; n(k,n) += 1; n(m) += 1; n(k) += 1;
    if converged then:
        compute θ;
        compute ψ;