随机二叉平衡树treap个人总结
二叉查找树
二叉查找树(Binary Search Tree),或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
二叉查找树代码很好写,这里就不过多介绍,现在分析二叉查找树的性能:二叉查找树在最坏情况下,可能退化成一条链,比如数据(1,2,3,4,5,6),如果开始以1为root来建二叉查找树那么这个树就是一条链,此时它的复杂度是O(n)的。
所以二叉查找树(BST)理想情况下是O(logn),最坏复杂度是O(n),因此我们需要让二叉查找树尽量的平衡,从而保证所有操作在O(logn)的时间复杂度下进行。
本文介绍其中的一种方法随机平衡二叉查找树(treap),当然也有许多其他的方法如:红黑树,SBT,伸展树,AVL树,其中treap的编码是最容易实现的。
1、什么是Treap
Treap (tree + heap) 在 BST 的基础上,添加了一个修正值。在满足 BST 性质的基础上,Treap 节点的修正值还满足最小堆性质。最小堆性质可以被描述为每个子树根节点都小于等于其子节点。于是,Treap 可以定义为有以下性质的二叉树:
1. 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值,而且它的根节点的修正值小于等于左子树根节点的修正值;
2. 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值,而且它的根节点的修正值小于等于右子树根节点的修正值;
3. 它的左、右子树也分别为 Treap。
1. 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值,而且它的根节点的修正值小于等于左子树根节点的修正值;
2. 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值,而且它的根节点的修正值小于等于右子树根节点的修正值;
3. 它的左、右子树也分别为 Treap。
修正值是节点在插入到 Treap 中时随机生成的一个值,它与节点的值无关,由随机函数rand()生成。
下面给出Treap的一般定义:
/*
*left,right为左右节点,key用来存储节点的实际数值,size表示当前节点的子节点个数,cnt表示当前节点有多少个相同的数值,如数据里有三个4则此时的cnt=3,fix就是修正值
*/
- struct Node
- {
- Node *left,*right;
- int key,size,cnt,fix;
- Node(int e) : key(e),size(1),cnt(1),fix(rand()) {}
- }*root,*null;
2、如何使treap平衡
Treap中的节点不仅满足BST的性质,还满足最小堆的性质。因此需要通过旋转来调整二叉树的结构,在维护Treap的旋转操作有两种:左旋和右旋,(注意:无论怎么旋转二叉查找树的性质是不能改变的)
2.1、 左旋
左旋后节点A变成节点B的父亲,但是可以看出BST的基本性质还是没有改变的。
注意:旋转节点为B,即把B的右子树旋转到左子树上
/*
*左旋代码
*/
- void left_rat(Node *&x)
- {
- Node *y = x->right;
- x->right = y->left;
- y->left = x;
- x = y;
- }
2.2、右旋
注意:旋转节点为B,即把B的左子树旋转到右子树上
/*
*右旋代码
*/
- void right_rat(Node *&x)
- {
- Node *y = x->left;
- x->left = y->right;
- y->right = x;
- x = y;
- }
3、查询操作
由于Treap也满足BST的性质,因此查找操作和BST的操作是一样的,这里不再介绍。
4、插入操作
在 Treap 中插入元素,与在 BST 中插入方法相似。首先找到合适的插入位置,然后建立新的节点,存储元素。但是要注意建立新的节点的过程中,会随机地生成一个修正值,这个值可能会破坏堆序,因此我们要根据需要进行恰当的旋转。具体方法如下:
1. 从根节点开始插入;
2. 如果要插入的值小于等于当前节点的值,在当前节点的左子树中插入,插入后如果左子节点的修正值小于当前节点的修正值,对当前节点进行右旋;
3. 如果要插入的值大于当前节点的值,在当前节点的右子树中插入,插入后如果右子节点的修正值小于当前节点的修正值,对当前节点进行左旋;
4. 如果当前节点为空节点,在此建立新的节点,该节点的值为要插入的值,左右子树为空,插入成功。
1. 从根节点开始插入;
2. 如果要插入的值小于等于当前节点的值,在当前节点的左子树中插入,插入后如果左子节点的修正值小于当前节点的修正值,对当前节点进行右旋;
3. 如果要插入的值大于当前节点的值,在当前节点的右子树中插入,插入后如果右子节点的修正值小于当前节点的修正值,对当前节点进行左旋;
4. 如果当前节点为空节点,在此建立新的节点,该节点的值为要插入的值,左右子树为空,插入成功。
时间复杂度O(logn)
下面举例说明:
- void insert(Node *&x ,int e)
- {
- if(x == null)
- {
- x = new Node (e);
- x->left = x->right = null;
- }
- else if(e < x->key)
- {
- insert(x->left,e);
- if(x->left->fix < x->fix) right_rat(x);
- }
- else if(e > x->key)
- {
- insert(x->right,e);
- if(x->right->fix < x->fix) left_rat(x);
- }
- else
- ++x->cnt;
- }
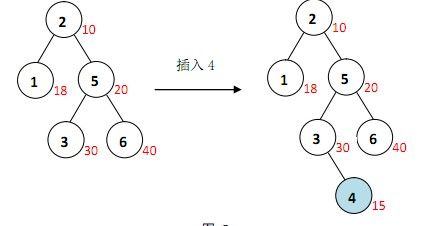
如下图,在已知的 Treap 中插入值为 4 的元素。找到插入的位置后,随机生成的修正值为 15(红色数值为修正值fix)
新建的节点 4 与他的父节点 3 之间不满足堆序(本文的堆序都是指最小顶堆),对以节点 3 为根的子树左旋
节点 4 与其父节点 5 仍不满足最小堆序,对以节点 5 为根的子树右旋
至此,节点 4 与其父亲 2 满足堆序,调整结束。
5、删除操作
按照在 BST 中删除元素同样的方法来删除 Treap 中的元素,即用它的后继(或前驱)节点的值代替它,然后删除它的后继(或前驱)节点。为了不使 Treap 向一边偏沉,我们需要随机地选取是用后继还是前驱代替它,并保证两种选择的概率均等。
情况一,该节点为叶节点或链节点,则该节点是可以直接删除的节点。若该节点有非空子节点,用非空子节点代替该节点的,否则用空节点代替该节点,然后删除该节点。
情况二,该节点有两个非空子节点。我们的策略是通过旋转,使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值,右旋该节点,使该节点降为右子树的根节点,然后访问右子树的根节点,继续讨论;反之,左旋该节点,使该节点降为左子树的根节点,然后访问左子树的根节点,继续讨论,知道变成可以直接删除的节点。
- void remove(Node *&x,int e)
- {
- if(x == null) return;
- if(e < x->key) remove(x->left,e);
- else if(e > x->key) remove(x->right,e);
- else if(--x->cnt <= 0)//找到数值等于e的节点,然后进行删除操作
- {
- if(x->left == null || x->right == null)
- {
- Node *y = x;
- x = (x->left != null)?x->left:x->right;
- delete y;
- }
- else
- {
- if(x->left->fix < x->right->fix)
- {
- right_rat(x);
- remove(x->right,e);
- }
- else
- {
- left_rat(x);
- remove(x->left,e);
- }
- }
- }
- }
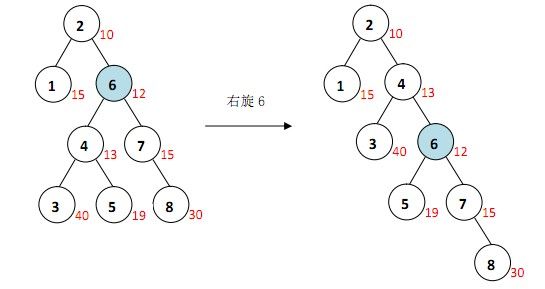
首先查找到6,发现节点 6 有两个子节点,且左子节点的修正值小于右子节点的修正值,需要右旋节点 6
旋转后,节点 6 仍有两个节点,右子节点修正值较小,于是左旋节点 6
此时,节点 6 只有一个子节点,可以直接删除,用它的左子节点代替它,删除本身
6、查找最大值和最小值
根据Treap的性质可以看出最左非空子节点就是最小值,同理最右非空子节点就是最大值(同样也是BST的性质)
- int findMin()
- {
- Node *x;
- for(x = root; x->left!=null; x=x->left);
- return x->key;
- }
- int findMax()
- {
- Node *x;
- for(x = root ; x->right!= null; x=x->right);
- return x->key;
- }
7、前驱与后继
定义:前驱,查找该元素在平衡树中不大于该元素的最大元素;后继查找该元素在平衡树中不小于该元素的最小元素。
从定义中看出,求一个元素在平衡树中的前驱和后继,这个元素不一定是平衡树中的值,而且如果这个元素就是平衡树中的值,那么它的前驱与后继一定是它本身。
求前驱的基本思想:贪心逼近法。在树中查找,一旦遇到一个不大于这个元素的值的节点,更新当前的最优的节点,然后在当前节点的右子树中继续查找,目的是希望能找到
一个更接近于这个元素的节点。如果遇到大于这个元素的值的节点,不更新最优值,节点的左子树中继续查找。直到遇到空节点,查找结束,当前最优的节点的值就是要求的前
驱。求后继的方法与上述相似,只是要找不小于这个元素的值的节点。
一个更接近于这个元素的节点。如果遇到大于这个元素的值的节点,不更新最优值,节点的左子树中继续查找。直到遇到空节点,查找结束,当前最优的节点的值就是要求的前
驱。求后继的方法与上述相似,只是要找不小于这个元素的值的节点。
算法说明:
求前驱:
1. 从根节点开始访问,初始化最优节点为空节点;
2. 如果当前节点的值不大于要求前驱的元素的值,更新最有节点为当前节点,访问当前节点的右子节点;
3. 如果当前节点的值大于要求前驱的元素的值,访问当前节点的左子节点;
4. 如果当前节点是空节点,查找结束,最优节点就是要求的前驱。
1. 从根节点开始访问,初始化最优节点为空节点;
2. 如果当前节点的值不大于要求前驱的元素的值,更新最有节点为当前节点,访问当前节点的右子节点;
3. 如果当前节点的值大于要求前驱的元素的值,访问当前节点的左子节点;
4. 如果当前节点是空节点,查找结束,最优节点就是要求的前驱。
求后继:
1. 从根节点开始访问,初始化最优节点为空节点;
2. 如果当前节点的值不小于要求前驱的元素的值,更新最有节点为当前节点,访问当前节点的左子节点;
3. 如果当前节点的值小于要求前驱的元素的值,访问当前节点的右子节点;
4. 如果当前节点是空节点,查找结束,最优节点就是要求的后继。
- // Predecessor
- Node* Pred(Node* x,Node* y,int e) {
- if (x == null)
- return y;
- if (e < x->key)
- return Pred(x->left,y,e);
- return Pred(x->right,x,e);
- }
- // Successor
- Node *Succ(Node *x,Node *y,int e)
- {
- if(x == null) return y;
- if(e <= x->key) return Succ(x->left,x,e);
- return Succ(x->right,y,e);
- }
- Node *p = Pred(root,null,e);
- Node *s = Succ(root,null,e);
根据前驱和后继的定义,我们还可以以此来查找某个元素与 Treap 中所有元素绝对值之差最小元素。如果按照数轴上的点来解释的话,就是求一个点的最近距离点。方法就是分别求出该元素的前驱和后继,比较前驱和后继哪个距离基准点最近。
求前驱、后继和距离最近点是许多算法中经常要用到的操作,Treap 都能够高效地实现。
8、当前节点子树的大小
Treap 是一种排序的数据结构,如果我们想查找第 k 小的元素或者询问某个元素在 Treap 中从小到大的排名时,我们就必须知道每个子树中节点的个数。我们称以一个子树的所有节点的权值之和,为子树的大小。由于插入、删除、旋转等操作,会使每个子树的大小改变,所以我们必须对子树的大小进行动态的维护。
对于 旋转,我们要在旋转后对子节点和根节点分别重新计算其子树的大小。
对于 插入,新建立的节点的子树大小为 1。在寻找插入的位置时,每经过一个节点,都要先使以它为根的子树的大小增加 1,再递归进入子树查找。
对于 删除,在寻找待删除节点,递归返回时要把所有的经过的节点的子树的大小减少 1。要注意的是,删除之前一定要保证待删除节点存在于 Treap 中。
下面给出左旋操作如何计算子树大小的代码,右旋很类似。
//这里需要注意的是,每个节点可能有重复的,重复的数目是用cnt来记录的,因此最后需要加上cnt
- void left_rat(Node *&x)
- {
- Node *y = x->right;
- x->right = y->left;
- y->left = x;
- x = y;
- y = x.left;//找到x的左子树
- if(y != null)
- {
- y.size = y.size + y.cnt;
- if(y.left != null) y.size += y.left.size;
- if(y.right != null) y.size += y.right.size;
- x.size += y.size;
- }
- x.size += x.cnt;
- if(x.right != null) x.size += x.right.size;
- }
9、查找第K小元素
首先,在一个子树中,根节点的排名取决于其左子树的大小,如果根节点有权值 cnt,则根节点 P 的排名是一个闭区间 A,且 A = [
P->left->size + 1,
P->left->size + P->cnt]。根据此,我们可以知道,如果查找排名第 k 的元素,k∈A,则要查找的元素就是 P 所包含元素。如果 k<A,那么排名第 k 的元素一定在左子树中,且它还一定是左子树的排名第 k 的元素。如果 k>A,则排名第 k 的元素一定在右子树中,是右子树排名第 k-(
P->left->size + P->cnt)的元素
算法思想:
1. 定义 P 为当前访问的节点,从根节点开始访问,查找排名第 k 的元素;
2. 若满足 P->left->size + 1 <=k <= P->left->size + P->cnt,则当前节点包含的元素就是排名第 k 的元素;
3. 若满足 k < P->left->size+ 1,则在左子树中查找排名第 k 的元素;
4. 若满足 k > P->left->size + P->cnt,则在右子树中查找排名第 k-( P->left->size + P->cnt)的元素。
- Node *Treap_Findkth(Node *P,int k)
- {
- if (k < P->left->size + 1) //左子树中查找排名第 k 的元素
- return Treap_Findkth(P->left,k);
- else if (k > P->left->size + P->cnt) //在右子树中查找排名第 k-(P->left->size + P->cnt)的元素
- return Treap_Findkth(P->right,k-(P->left->size + P->cnt));
- else
- return P; //返回当前节点
- }
10、求某个元素的排名
算法思想:
1. 定义 P 为当前访问的节点,cur 为当前已知的比要求的元素小的元素个数。从根节点开始查找要求的元素,初始化 cur 为 0;
2. 若要求的元素等于当前节点元素,要求的元素的排名为区间[P->left->size + cur + 1, P->left->size + cur + P->cnt]内任意整数;
3. 若要求的元素小于当前节点元素,在左子树中查找要求的元素的排名;
4. 若要求的元素大于当前节点元素,更新 cur 为 cur + P->left->size+P->cnt,在右子树中查找要求的元素的排名。
2. 若要求的元素等于当前节点元素,要求的元素的排名为区间[P->left->size + cur + 1, P->left->size + cur + P->cnt]内任意整数;
3. 若要求的元素小于当前节点元素,在左子树中查找要求的元素的排名;
4. 若要求的元素大于当前节点元素,更新 cur 为 cur + P->left->size+P->cnt,在右子树中查找要求的元素的排名。
- int Treap_Rank(Treap_Node *P,int value,int cur) //求元素 value 的排名
- {
- if (value == P->value)
- return P->left->size + cur + 1; //返回元素的排名
- else if (value < P->value) //在左子树中查找
- return Treap_Rank(P->left,value,cur);
- else //在右子树中查找
- return Treap_Rank(P->right,value,cur + P->left->size + P->cnt);
- }
- rank=Treap_Rank(root,8,0);
Treap主要运用于动态的数据统计中,例如区间第K小值的问题(POJ 2761),利用前驱与后继来 查找某个元素与 Treap 中所有元素绝对值之差最小元素。
原文来自:http://blog.csdn.net/acceptedxukai/article/details/6910685