重学数据结构系列之——二叉树基础

1.二叉树

1.定义

每棵树有且仅有一个树根

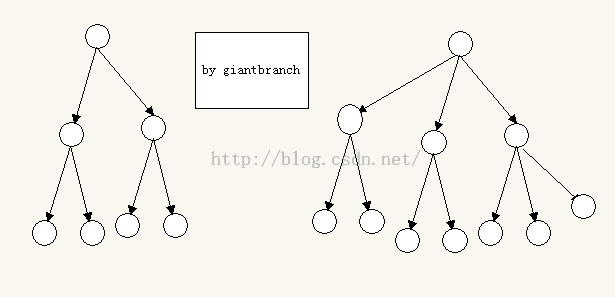
左边就是一个二叉树（二叉树的每个结点最多只有两个孩子结点，也就是说每个结点最多有两个子树），右边是不确定是不是叫三叉树

其实我们的计算机的目录结构就像一棵树 

2.实现

下面这个是储存int类型的二叉树，既可以int，又可以char请看最底部的代码

#include <iostream>
using namespace std;

//结点类
class Node{
public:
	//数据
	int data;
	//左孩子和右孩子
	Node *lchild, *rchild;
	Node(int _data){
		data = _data;
		lchild = NULL;
		rchild = NULL;
	}
	~Node(){
		if (lchild != NULL) {
			delete lchild;
		}
		if (rchild != NULL) {
			delete rchild;
		}
	}
	//先序遍历（先自己再左右，可以看到下面的顺序也是这样）
	void preorder(){
		//输出当前结点的数据域
		cout<<data<<" ";
		//左不为空，则递归调用先序遍历
		if (lchild != NULL) {
			lchild->preorder();
		}
		//右不为空，也递归调用先序遍历
		if (rchild != NULL) {
			rchild->preorder();
		}
	}
	//中序遍历（先左，再中，再右）
	void inorder(){
		if (lchild != NULL) {
			lchild->inorder();
		}
		cout<<data<<" ";
		if (rchild != NULL) {
			rchild->inorder();
		}
	}
	//后序遍历（先左右，再中间）
	void postorder(){
		if (lchild != NULL) {
			lchild->postorder();
		}
		if (rchild != NULL) {
			rchild->postorder();
		}
		cout<<data<<" ";
	}
	//根据先序，中序构建一颗二叉树
	//pre_str:先序遍历的字符串（如124536）
	//in_str:中序遍历的字符串
	//len：（先序）中序遍历的字符串的长度
	Node* build(const string &pre_str, const string &in_str, int len){
		//先序遍历的第一位（pre_str[0]）就是根结点，先构建根结点
		//pre_str[0] - '0':因为我们这里用的数据域只是数字0-9，减去字符'0'就是实际的数字，其实就是他们的ASCII相减，你可以输出一下'9'-'0'是不是 9
		Node *p = new Node(pre_str[0] - '0');
		//查找中序遍历中根节点的位置（根结点左边的都是左子树的，右边的都是右子树）
		int pos = in_str.find(pre_str[0]);
		//左子树不为空，构建左子树
		if (pos > 0) {
			//以根结点的左子树作为新的根结点去构建即可
			//其中左子树结点有pos个，先序中第一个是根结点，所以substr(1,pos)【表示从索引1开始，截取pos个字符】就是左子树的先序遍历
			//in_str.substr(0,pos):从索引0开始，截取pos个字符
			p->lchild = build(pre_str.substr(1,pos), in_str.substr(0,pos), pos);
		}
		//右子树不为空，构建右子树
		if (len - pos -1 > 0) {
			//其中右子树结点有len - pos -1个，先序中第一个是根结点，跟着是pos个左子树的，所以substr(pos+1)【表示从索引pos+1到字符串的最后】就是右子树先序遍历
			//in_str.substr(pos+1):从索引pos+1开始到字符串的最后
			p->rchild = build(pre_str.substr(pos+1), in_str.substr(pos+1), len - pos -1);
		}
		//构建完成,返回二叉树
		return p;
	}
};

class BinaryTree{
private:
	//树的根，就是最上面的结点
	Node *root;
public:
	//无参构造函数
	BinaryTree(){
		//一开始是一颗没结点的树--空树
		root = NULL;
	}
	//已知先序，中序遍历的构造函数
	BinaryTree(const string &pre_str, const string &in_str, int len){
		root = root->build(pre_str, in_str, len);
    }
	~BinaryTree(){
		if (root != NULL) {
			delete root;
		}
	}
	//构建一个简单的二叉树以便测试
	void build_demo(){
		root = new Node(1);
		root->lchild = new Node(2);
		root->rchild = new Node(3);
		root->lchild->lchild = new Node(4);
		root->lchild->rchild = new Node(5);
		root->rchild->rchild = new Node(6);
		
	}
	//先序遍历
	void preorder(){
		root->preorder();
	}
	//中序遍历
	void inorder(){
		root->inorder();
	}
	//后序遍历
	void postorder(){
		root->postorder();
	}
};



int main(){
	BinaryTree binarytree;
	binarytree.build_demo();
	cout<<"先序遍历"<<endl;
	binarytree.preorder();
	cout<<endl;
	cout<<"中序遍历"<<endl;
	binarytree.inorder();
	cout<<endl;
	cout<<"后序遍历"<<endl;
	binarytree.postorder();
	cout<<endl<<endl;
	
	cout<<"根据先序中序构建二叉树并输出后续遍历结果"<<endl;
	string pre_str = "136945827";
    string in_str = "963548127";
	BinaryTree binarytree2(pre_str, in_str, in_str.length());
	binarytree2.postorder();
	cout<<endl;

	return 0;
}

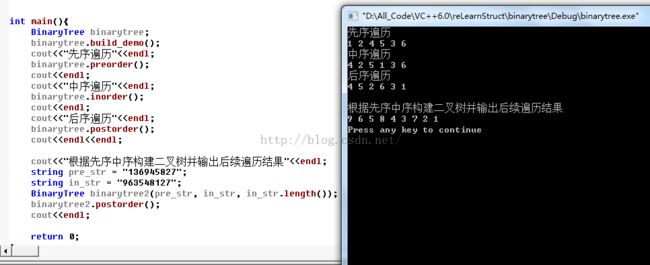
3.运行结果

2.解决一个小问题：二叉树左右对调（镜像）

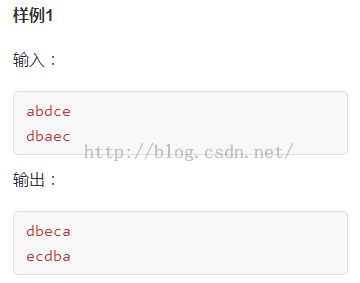
1.描述

已知先序和中序，输出原二叉树的后序和左右对调后（就是镜像）的后序遍历

2.代码实现

#include <iostream>
#include <string>
using namespace std;

//结点类
template<class Type> class Node{
public:
	//数据
	Type data;
	//左孩子和右孩子
	Node *lchild, *rchild;
	Node(Type _data){
		data = _data;
		lchild = NULL;
		rchild = NULL;
	}
	~Node(){
		if (lchild != NULL) {
			delete lchild;
		}
		if (rchild != NULL) {
			delete rchild;
		}
	}
	//先序遍历（先自己再左右，可以看到下面的顺序也是这样）
	void preorder(){
		//输出当前结点的数据域
		cout<<data<<"";
		//左不为空，则递归调用先序遍历
		if (lchild != NULL) {
			lchild->preorder();
		}
		//右不为空，也递归调用先序遍历
		if (rchild != NULL) {
			rchild->preorder();
		}
	}
	//中序遍历（先左，再中，再右）
	void inorder(){
		if (lchild != NULL) {
			lchild->inorder();
		}
		cout<<data<<"";
		if (rchild != NULL) {
			rchild->inorder();
		}
	}
	//后序遍历（先左右，再中间）
	void postorder(){
		if (lchild != NULL) {
			lchild->postorder();
		}
		if (rchild != NULL) {
			rchild->postorder();
		}
		cout<<data<<"";
	}
	//根据先序，中序构建一颗二叉树
	//pre_str:先序遍历的字符串（如124536）
	//in_str:中序遍历的字符串
	//len：（先序）中序遍历的字符串的长度
	Node* build(const string &pre_str, const string &in_str, int len){
		Node<Type> *p;
		//先序遍历的第一位（pre_str[0]）就是根结点，先构建根结点
		if (pre_str[0]>='0' && pre_str[0]<='9') {
		//如果是数字类型
			p = new Node<Type>(pre_str[0]-'0');
		}else{
			p = new Node<Type>(pre_str[0]);
		}
		//Node<Type> *p = new Node<Type>(pre_str[0]);
		//查找中序遍历中根节点的位置（根结点左边的都是左子树的，右边的都是右子树）
		int pos = in_str.find(pre_str[0]);
		//左子树不为空，构建左子树
		if (pos > 0) {
			//以根结点的左子树作为新的根结点去构建即可
			//其中左子树结点有pos个，先序中第一个是根结点，所以substr(1,pos)【表示从索引1开始，截取pos个字符】就是左子树的先序遍历
			//in_str.substr(0,pos):从索引0开始，截取pos个字符
			p->lchild = build(pre_str.substr(1,pos), in_str.substr(0,pos), pos);
		}
		//右子树不为空，构建右子树
		if (len - pos -1 > 0) {
			//其中右子树结点有len - pos -1个，先序中第一个是根结点，跟着是pos个左子树的，所以substr(pos+1)【表示从索引pos+1到字符串的最后】就是右子树先序遍历
			//in_str.substr(pos+1):从索引pos+1开始到字符串的最后
			p->rchild = build(pre_str.substr(pos+1), in_str.substr(pos+1), len - pos -1);
		}
		//构建完成,返回二叉树
		return p;
	}
	Node* buildMirror(const string &pre_str, const string &in_str, int len){
		Node<Type> *p;
		if (pre_str[0]>='0' && pre_str[0]<='9') {
			p = new Node<Type>(pre_str[0]-'0');
		}else{
			p = new Node<Type>(pre_str[0]);
		}
		int pos = in_str.find(pre_str[0]);
		if (pos > 0) {
			p->rchild = buildMirror(pre_str.substr(1,pos), in_str.substr(0,pos), pos);
		}
		if (len - pos -1 > 0) {
			p->lchild = buildMirror(pre_str.substr(pos+1), in_str.substr(pos+1), len - pos -1);
		}
		return p;
	}

};

template<class Type> class BinaryTree{
private:
	//树的根，就是最上面的结点
	Node<Type> *root;
public:
	//无参构造函数
	BinaryTree(){
		//一开始是一颗没结点的树--空树
		root = NULL;
	}
	//已知先序，中序遍历的构造函数
	BinaryTree(const string &pre_str, const string &in_str, int len){
		root = root->build(pre_str, in_str, len);
    }
	~BinaryTree(){
		if (root != NULL) {
			delete root;
		}
	}
	
	//先序遍历
	void preorder(){
		root->preorder();
	}
	//中序遍历
	void inorder(){
		root->inorder();
	}
	//后序遍历
	void postorder(){
		root->postorder();
	}
	//构建镜像二叉树
	void buildMirror(const string &pre_str, const string &in_str, int len){
		root = root->buildMirror(pre_str, in_str, len);
	}
};



int main(){
	string pre_str;
    string in_str;
	cin>>pre_str>>in_str;
	BinaryTree<char> binarytree(pre_str, in_str, in_str.length());
	binarytree.postorder();
	cout<<endl;
	binarytree.buildMirror(pre_str, in_str, in_str.length());
	binarytree.postorder();
	cout<<endl;
	return 0;
}

3.运行结果