ML—SVM讲义
华电北风吹
天津大学认知计算与应用重点实验室
日期:2015/10/23
本篇博客主要讲解我自己理解的SVM。
一、SVM核心
对于线性可分的数据,SVM指导思想是寻找一个分类超平面,使得样本同一类的被分在超平面同侧的同时,使得两侧距离分类超平面最近的点的距离最大。这些点被称作支持向量。
假设n维空间的分类超平面是 wTx+b=0 。则任意一点(x,y)到这个超平面的距离为 |wTx+b|||w||2 。
而SVM的目标就是寻找可以正确区分所有样本的w,b,并使得对于任意一个支持向量(x,y)有
max|wTx+b|||w||2(1-1)
由于同一个分类超平面w,b可以成比例的放缩。因此总可以经过适当的放缩找到合适的w,b使得支持向量处的 wTx+b 值为1或-1。所以这时目标公式(1)就简化为
max1||w||2(1-2)
而此时的约束条件可以表达为
yi(wTxi+b)≥1,i=1,2,...,m(1-3)
在实际应用过程中一般采用的(1-2)的另一种等价凸函数形式,见公式(1-4),因此问题转化为(1-4,5)。
min12||w||2(1-4)
yi(wTxi+b)≥1,i=1,2,...,m(1-5)
二、最优间隔分类器
想要理解接下来这一部分需要先看懂参考博客[1]。
我们先把SVM模型公式(1-4,5)转化为约束优化的标准形式。
minf(w,b)=12||w||2(2-1)
gi(w,b)=1−yi(wTxi+b)≤0,i=1,2,...,m(2-2)
此时的拉格朗日函数为
L(w,b,α)=12||w||2+∑mi=1αigi(w,b)=12||w||2+∑mi=1αi(1−yi(wTxi+b))(2-3)
很显然 f(w,b),gi(w,b) 满足KKT条件的凸函数要求,由于没有等式约数,所以根据KKT条件可知,必然存在 w∗,b∗,α∗ 满足参考博客[1]中所说的KKT条件的5个等式(由于没有不等式约束实际上为4个)。
根据参考博客的公式(k1)得:
∂∂wL(w,b,α)=w−∑mi=1αiyixi=0(2-4)
∂∂bL(w,b,α)=∑mi=1αiyi=0(2-5)
由公式(2-4)可得
w=∑mi=1αiyixi(2-6)
将公式(2-5,6)带入公式(2-3)可将公式(2-3)转化为
L(w,b,α)=∑mi=1αi−12∑mi=1∑mj=1αiαjyiyj<xi,xj>(2-7)
这时对偶问题的定义为
θD(α)=minw,bL(w,b,α)=∑mi=1αi−12∑mi=1∑mj=1αiαjyiyj<xi,xj>(2-8)
对偶问题转化为
maxθD(α)=∑mi=1αi−12∑mi=1∑mj=1αiαjyiyj<xi,xj>(2-9)
这时的约束条件应该为
注:公式(2-4~10)的推导过程需要一点说明,最起码我个人是这样认为的,公式(2-4,5)是KKT条件得出来的,因此这时候公式里面的 w,b,α 应该为 w∗,b∗,α∗ ,直到公式(14,15)都应该是这样。在这里采用 w,b,α 是因为在求解公式(2-1,2)的对偶问题的时候,发现在KKT条件成立的条件下发现 θD(α)=minw,bL(w,b,α) 可以容易消去 w和b 。因此接下来需要满足 α 的限制条件下求最优值即可。
并且,很容易得到
b∗=−12(maxyi=−1w∗xi+minyi=1w∗xi)(2-11)
SVM判别函数为
wTx=(∑mi=1αiyixi)Tx+b=∑mi=1αiyi<xi,x>+b(2-12)
property-1. 通过公式(2-12)我们发现对测试样本做预测的时候我们只需要知道 αi 即可。
property-2. 根据参考博客kkt-3, α∗i>0的时候必有gi(w∗,b∗)=0,若gi(w∗,b∗)<0,必有α∗i=0 。
property-3. 我们的SVM训练已经转化为公式(2-9,10),SVM预测转化为公式(11,12)。我们发现模型整个算法(模型训练和模型预测)是与输入样本之间特征的内积有关。这个性质是SVM的核技巧的基础。
三、核技巧
核技巧是寄希望于通过将原始的n维向量内积扩展到更高维的空间上的内积,使得在n维空间中线性不可分的数据在高维空间变得线性可分。
例如,图一所示为二维空间的线性不可分样本

但是如果在三维空间是如图二所示的话
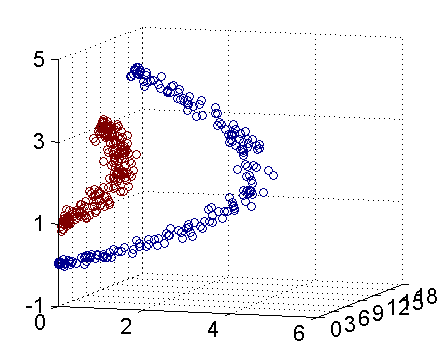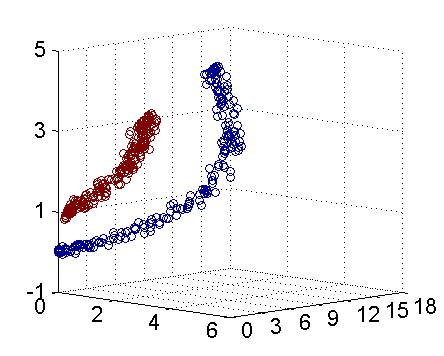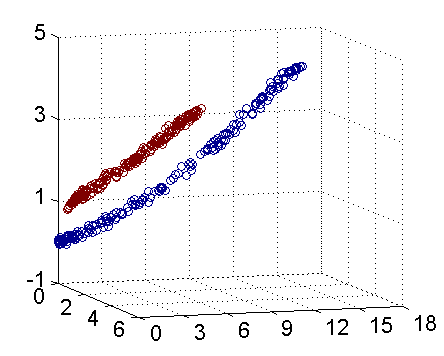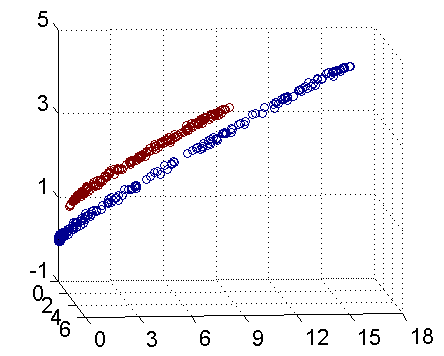
这样通过把二维数据扩展到三维数据就达到了线性可分的目的。不得不说这是核函数表现比较理想的情况,但是这给我们解决线性不可分问题提供了一种解决办法。
目前常用的核函数有
1) 线性核函数
K(x,z)=<x,z>
2) 多项式核函数
K(x,z)=(k0<x,z>+b0)n
3) 径向基(RBF核)函数
K(x,z)=exp(−||x−z||22σ2)
4)单极性(sigmoid)核函数
K(x,z)=tanh(k0<x,z>+b0)
四、惩罚法
前面说的都是针对线性可分的数据。现实中遇到的数据大都是线性不可分的。对于线性不可分的数据,可以使用核函数来解决,但是核函数并不一定能够保证升维以后就是线性可分的,因此就有了C-SVC。
C-SVC模型表述如下:
min12||w||2+C∑mi=1ξi(4-1)
yi(wTxi+b)≥1−ξi,i=1,2,...,m(4-2)
根据与线性可分时同样的对偶方法及KKT条件可以得到对偶形式为:
maxθD(α)=∑mi=1αi−12∑mi=1∑mj=1αiαjyiyj<xi,xj>(4-3)
约束条件应该为:
五、SMO算法
由于日常的数据大多不可分的,C-SVC已经成为SVM的标准形式,接下来主要讨论怎么使用SMO算法来求解模型(4-3,4)里面的 αi 。注意到随机梯度上升法在求解最优值的时候的高效,SMO使用随机梯度上升法求解 αi 。
在迭代的过程中,每一次选择一对 αi 和 αj ,其它的 αk 在本次梯度上升迭代过程中不做变化。由于公式(4-4)里面 ∑mi=1αiyi=0 可得
αi+αj=−∑mk=1,k≠i,k≠jαkyk=ζ(5-1)
结合 0≤αi≤C,0≤αj≤C

如图所示,可以求解 L≤αi≤H ,接下来只要把公式(4-3,4)里面的 αj 利用公式(5-1)替换为 αi ,便很容易求解是的公式(4-3)取最大时的 αi,αj ,然后对 αi,αj 值进行更新,进入下一次梯度上升过程即可。
参考博客:
1、ML—SVM预热之拉格朗日对偶和KKT条件
http://blog.csdn.net/zhangzhengyi03539/article/details/49366447
2、ML—核技巧
http://blog.csdn.net/zhangzhengyi03539/article/details/49821027