普林斯顿大学算法第一周个人总结1

转载自：revilwang 

来自普林斯顿大学 的 Coursera 课程《算法，第一部分》 ，课程地址：https://www.coursera.org/course/algs4partI

第一周的内容是 Union-Find算法和算法分析两个部分，这一篇只总结Union-Find。

问题描述：

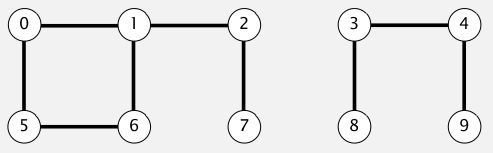
有N个元素，从 0 ~ N-1 编号，假设用通路表示元素之间的连接，当执行多次任意两个元素的连接之后，如何判断某两个元素是否能够通过已有路径相连通。连接的动作我们称之为 union，判断两元素是否相连的操作称之为 find，类比下图：

从图上可以看出，0, 1, 2, 5, 6, 7 中任意两个元素都是相连的，同样 3, 4, 8, 9 中任意两个元素也是互连的，但是第一个集合和第二个集合的元素却是无法连通的。

实际操作中可用于在一个庞大的网路环境下，如何迅速判断某两个点是否相连，如下图：

开发有效算法的步骤：

1） 构建模型
2） 寻找算法
3） 方法的效率和内存使用
4） 效率差，内存使用率高，找出问题的原因所在
5） 寻找解决方法重复3

首先确认 union 和 find 操作应该满足什么样的条件：

find操作：确认两个对象是否连接：
a. p连接到q
b. p连接到q，则q也连接到p
c. p连接到q，q连接到r，则p也连接到r
union操作：连接在一起的对象，我们统称为一个连接集合，执行一次union操作就相当于将两个对象所在的集合连接到一起，组成一个新的集合。新集合中的任意两个成员也应该都处于连接状态。

然后寻找合适的算法：

演示三种算法，循序渐进，展示算法的优化过程

原课程是采用 Java，在这里我将 Java 的实现修改为 C 实现。

（1）Quick-find

数据结构：采用简单的一维数组。

struct qf {
    int*    qf_array;
    int     count;
};

struct qf {
    int*    qf_array;
    int     count;
};

算法描述：当且仅当p和q具有相同的ID，则p和q处于连接状态
find：     查看两个数组成员是否具有相同ID
union： 将所有和 id[p] 相同 ID 值的数组成员的值，全部转换为 id[q] 的ID值。

图示算法的效果：

算法实现：

int qf_union(QuickFind qf, int p, int q)
{
    int i, pid, qid;

    pid = qf->qf_array[p];
    qid = qf->qf_array[q];
    for (i = 0; i < qf->count; i++)
        if (qf->qf_array[i] == pid)
            qf->qf_array[i] = qid;
    return 0;
}

int qf_connected(QuickFind qf, int p, int q)
{
    return qf->qf_array[p] == qf->qf_array[q];
}

int qf_union(QuickFind qf, int p, int q)
{
    int i, pid, qid;

    pid = qf->qf_array[p];
    qid = qf->qf_array[q];
    for (i = 0; i < qf->count; i++)
        if (qf->qf_array[i] == pid)
            qf->qf_array[i] = qid;
    return 0;
}

int qf_connected(QuickFind qf, int p, int q)
{
    return qf->qf_array[p] == qf->qf_array[q];
}

算法效率：
        a. 初始化：N
        b.  union：N
        c.  find：1

算法总结：
Quick-find 有一个很严重的问题，对 N 个元素执行 N 次 union 操作，数组访问次数就是 N^2 次，当N变得很大的时候，效率会很差。

（2）Quick-Union

数据结构：采用和 Quick-find 一样简单的一维数组

struct qu {
    int*    qu_array;
    int     count;
};

struct qu {
    int*    qu_array;
    int     count;
};

算法描述：若p和q具有相同的根元素，则p和q 处于连接状态。根元素的标识为 id[p] = p
find：     查看p和q是否具有相同的根元素
union： 将p的根元素修改为q的根元素

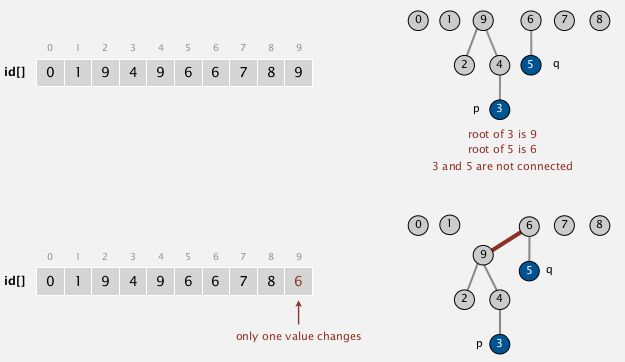
算法实现图示：

算法实现：

static int root(QuickUnion qu, int i)
{
    while (qu->qu_array[i] != i)
        i = qu->qu_array[i];
    return i;
}

int qu_union(QuickUnion qu, int p, int q)
{
    int proot, qroot;

    proot = root(qu, p);
    qroot = root(qu, q);
    qu->qu_array[proot] = qroot;
    return 0;
}

int qu_connected(QuickUnion qu, int p, int q)
{
    return root(qu, p) == root(qu, q);
}

static int root(QuickUnion qu, int i)
{
    while (qu->qu_array[i] != i)
        i = qu->qu_array[i];
    return i;
}

int qu_union(QuickUnion qu, int p, int q)
{
    int proot, qroot;

    proot = root(qu, p);
    qroot = root(qu, q);
    qu->qu_array[proot] = qroot;
    return 0;
}

int qu_connected(QuickUnion qu, int p, int q)
{
    return root(qu, p) == root(qu, q);
}

算法效率：初始化、union和find均为N的操作

算法总结：

Quick-Union 算法对 union 操作进行了优化，即使是对 N 个元素执行 N 次 union，数组的访问次数最多也是 N。但是 union 和 find 都会从节点遍历到根元素，如果每次的 union 操作都是将一个大树的根元素连接到另一个只有单一元素（也就是自己本身就是根元素）的树，那么很容易出现“高树”的现象。最差的时候，两个都会是 N 的操作。

（3）Weighted-Quick-Union

数据结构：N个元素的一维数组，加上辅助的树大小的数组。

struct qu {
    int*    qu_array;
    int*    size;
    int     count;
};

struct qu {
    int*    qu_array;
    int*    size;
    int     count;
};

算法描述：在Quick-union的基础上加以修改，记录树的大小，总是将较小树的根连接到较大树的根，避免出现“高树”现象
find：    查看p和q是否具有相同的根
union： 在Quick-union的基础上，加入一个记录树大小的数组，保证每次都是小树根连接到大树根上

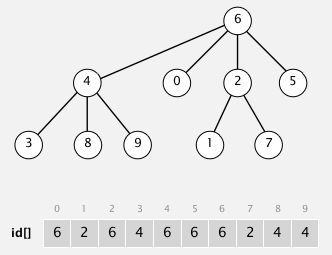
算法实现图示：

算法实现（find和Quick-Union一样，只演示 union 操作）：

int qu_union(QuickUnion qu, int p, int q)
{
    int proot, qroot;

    proot = root(qu, p);
    qroot = root(qu, q);
    if (qu->size[proot] < qu->size[qroot]) {
        qu->qu_array[proot] = qu->qu_array[qroot];
        qu->size[qroot] += qu->size[proot];
    } else {
        qu->qu_array[qroot] = qu->qu_array[proot];
        qu->size[proot] += qu->size[qroot];
    }
    return 0;
}

int qu_union(QuickUnion qu, int p, int q)
{
    int proot, qroot;

    proot = root(qu, p);
    qroot = root(qu, q);
    if (qu->size[proot] < qu->size[qroot]) {
        qu->qu_array[proot] = qu->qu_array[qroot];
        qu->size[qroot] += qu->size[proot];
    } else {
        qu->qu_array[qroot] = qu->qu_array[proot];
        qu->size[proot] += qu->size[qroot];
    }
    return 0;
}

算法效率：初始化：2N，union：已知根元素的情况下，效率为恒定值，find：与树的深度成正比，但是树的深度最大也只是lgN（证明过程略）。因此最差的情况下，union和find也都是 lgN。

不过 Weighted-Quick-Union 还可以继续改进，压缩从某一个节点到根的路径，将树进行更为平坦的伸展：

把查找根元素 root 的实现进行优化，实现方式有两种：
a. 增加一个for循环，将从某个节点到根节点路上的所有节点都直接连接到根节点
b. 将路径上每个节点的爷爷节点连接到根节点，只将路径减半

以 b 为例，修改 root 的操作如下：

static int root(QuickUnion qu, int i)
{
    while (qu->qu_array[i] != i) {
        qu->qu_array[i] = qu->qu_array[qu->qu_array[i]];
        i = qu->qu_array[i];
    }
    return i;
}

static int root(QuickUnion qu, int i)
{
    while (qu->qu_array[i] != i) {
        qu->qu_array[i] = qu->qu_array[qu->qu_array[i]];
        i = qu->qu_array[i];
    }
    return i;
}

这样每次 root 执行之后，路径都会减半，加快查找效率。

算法效率的演示在下篇总结。