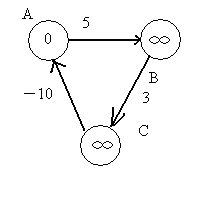
(六) 图算法
第二十二章 图的基本算法
计算机中图两种最普遍的表示法:邻接表表示和邻接矩阵表示
图的表示
图分为有向图和无向图,两种都可以表示为G={V,E},分别是顶点和边,有向无向均是针对边来说的。
一般稀疏的图用邻接表表示,而稠密的用邻接矩阵表示
邻接表:包含图G中每个和定点u相邻的定点(或者它可能包含指向这些定点的指针)每个邻接表的定点一般以任意顺序存储。
邻接表表示有个很好的特性:其存储空间为
不足之处:如果要确定图中边(u,v)是否存在,只能在定点u的邻接表中Adj[u]中搜索u。而邻接矩阵可以弥补这一缺点。
邻接矩阵:
如果G是一个有向图,则所有邻接表的长度之和为|E|,如果为无向图,则所有邻接表的长度之和为2|E|
广度优先搜索(BFS--breadth first search)
Bfs(G,s)
{
for each vertex u ∈V[G]-{s}
do color[u] = white
d[u] = ∞
π[u] = Nil
color[s] = gray
d[s] = 0
π[s] = Nil
Q = ? (空集)
Enqueue(Q,s)
while Q != ?
do u = Dequeue(Q)
for each v ∈Adj[u]
do if color[v] = white
then color[v] = gray
d[v] = d[v]+1
π[v] = u
Enqueue(Q,v)
color[v] = black
}
采用聚集分析得到:初始化操作开销为O(V),邻接表所花费的全部时间是O(E),故BFS总的运行时间是O(V+E)
最短路径
广度优先树
过程BFS在搜素图的同时,也建立了一棵广度优先树,并且对所有的v∈V(π),在G(π)中都有唯一的从s到v的简单路径,该路径也是G中从s到v的一条最短路径。
当BFS 从图G中某个源节点s开始执行后,前趋子图即构造成一棵广度优先树。
深度优先搜索(DFS)
Dfs(G)
{
for each vertex u ∈V[G]
do color[u] = white
π[u] = Nil
time = 0
for each vertex u ∈V[G]
do if color[u] = white
then Dfs-visit(u)
}
Dfs-visit(u)
{
color[u] = gray//white vertex u hai been discovered
time = time +1
d[u] =time
for each v ∈Adj[u]//Explore edge(u,v)
do if color[v] = white
then π[v] = u
Dfs-visit(v)
color[u] = black//blacken u ;it is finished
f[u] = time = time+1
} DFS的运行时间是:
深度优先搜索的性质:1)他的先辈子图G(π)形成一个由树所组成的森林。
2)发现和完成时间具有括号结构
白色路径定理:在一个(有向或者无向)图G=(G,V)的深度优先森林中,定点v是定点u的后裔,当且仅当在搜索过程中于时刻d[u]发现u时,可以从定点u出发,经过一挑完全由白色顶点组成的路径达到v。
DFS中碰到的四种边的分类以及识别算法:
算法思想描述:可以对算法DFS做一些修改,使之遇到图中的边时,对其进行分类,算法核心思想在对于每条边u,v,当该边被第一次寻到时,根据所到达顶点的颜色,对其分类。
1、白色的表明是树边
2、灰色的表明是回边
3、黑色的表明是正向边或者交叉边
如果du<dv正向边,du>dv交叉边
对于一个有向无回路图(有时称dag)进行拓扑排序。有向无回路图用于说明事件发生的先后次序。
Topological-sort(G)
{
call Dfs(G) to compute finishing times f[v] for each vertex v
as each vertex is finished ,insert it onto the front of a linked list
return the linked list of vertices
}
拓扑排序的运行时间是:
强连通分支
深度优先搜索一个经典应用:将一个有向图分解成各强连通分支。
两种深度优先搜索过程来进行分解
Strongly-connected-components(G)
{
call Dfs(G) to compute finishing times f[u] for each vertex u
compute G^T //G的转置矩阵
call Dfs(G^T).but in the main loop of Dfs,consider the vertices in order of decreasing f[u](as computed in line 1)
output the vertices of each tree in the depth-first forest formed in line 3 as a separete strongly connected component
}
第二十三章 最小生成树(最小权值生成树)
解决最小生成树问题的两种算法:Kruskal算法 和 Prim算法
两中算法都使用普通的二叉堆,很容易达到O(ElgV),而采用斐波那契堆,Prim算法运行时间可以减少到O(E+VlgV),且两个算法都是贪心算法。
最小生成树的形成
“通用”的最小生成树的算法
Generic-mst(G,w)
{
A = Nil
while A does not form a spanning tree
do find an edge(u,v) that is safe for A
A = A∪{(u,v)}
return A
}
无向图G=(V,E)的一个割(S,V-S)是对V的一个划分。如果某条边的权值是通过一个割的所有边中最小的,那么称该边为通过这个割的一条轻边。
识别安全边的一条规则:设图G=(V,E)是一个无向连通图,并且在E上定义了一个具有实数值的加权函数w。设A是E的一个子集,它包含于G的某个最小生成树。设割(S,V-S)是G的任意一个不妨害A的割,且边(u,v)是通过割(S,V-S) 的一条轻边,则边(u,v)对集合A来说是安全的。
Kruskal算法
类似于计算连通分支算法,它采用了一种不相交集合数据结构,以维护几个互相不相交的元素集合。
Mst-kruskal(G,w)
{
A = Nil
for each vertex v ∈V[G]
do Make-set(v)
sort the edges of E into nondecreasing order by weight w
for each edge(u,v)∈E,taken in nondecreasing order by weight
do if Find-set(u) != Find-set(v)
then A = A∪{(u,v)}
Union(u,v)
return A
}
Prim算法
Mst-Prim(G,w,r)
{
for each u ∈V[G]
do key[u] = ∞
π[u] = Nil
key[r] = 0
Q = V[G]
while Q != Nil
do u = Extract-min(Q)
for each v ∈ Adj[u]
do if v ∈Q and w(u,v) < key[v]
then π[v] = u
key[v] = w(u,v)
}
和kruskal算法不同,Prim算法总是形成单棵树。树从任意顶点r开始形成,并逐渐生成,直至该树覆盖了图中所有的顶点。在每一步,新加入的都是以生成树的顶点为起点,并且权值最小的边,因此Prim算 法也是贪心的。当算法终止时,最小生成树也就完成了。其过程如图所示:

第二十四章 单源最短路径
在最短路径问题中,给出的是一个带权的有向图G=(V,E),加权函数w:E--->R为从边到实型权值的映射。
路径p={v0,v1,...,vk}的权是指其组成边的所有权值之和:
定义从u到v间的最短路径的权为:
从定点u到定点v的最短路劲定义为权w(p) =
单源最短路径的变体
变体:1)单终点最短路径问题
2)单对顶点最短路径问题
3)每对顶点间最短路径问题
最短路径的最优子结构
最短路径算法依赖一种性质,就是一条两顶点间的最短路径包含路径上其他的最短路径。这种最优子结构性质是动态规划和贪心算法方法适用的一种标记。
Dijkstra算法是一个贪心算法,找出顶点对之间的最短路径Floyd-warshall算法是一个动态规划算法
负权值边
如果图G=(V,E)不包含从源s可达的负权回路,则对所有v∈V,最短路径的权定义![]() 依然正确,即使他是一个负值也是如此。
依然正确,即使他是一个负值也是如此。
回路
0权回路
最短路径的表示
松弛技术
对每个定点v∈V,都设置一个属性d[v],用来描述从源点s到v的最短路径上的权值的上界,称为最短路径估计。
对最短路径估计进行初始化:
Initialize-single-source(G,s)
{
for each vertex v ∈V[G]
do d[v] = ∞
π[v] = Nil
d[s] = 0
}
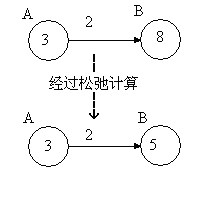
对边(u,v)进行了一步松弛操作
Relax(u,v,w)
{
if d[v] > d[u]+w(u,v)
then d[v] = d[v]+ w(u,v)
π[v] = u
}
最短路径以及松弛的性质
三角不等式
上界性质
无路径性质
收敛性质
路径松弛性质
前趋子图性质
Bellman-ford 算法
用来解决一般(边的权值可以为负)的单源最短路径问题
Bellman-ford(G,w,s)
{
Initialize-single-source(G,s)
for i = 1 to |v[G]|-1
do for each edge(u,v)∈E[G]
do Relax(u,v,w)
for each edge(u,v)∈E[G]
do if d[v]>d[u]+w(u,v)
then return FALSE
return TRUE
}
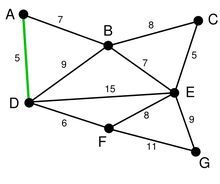
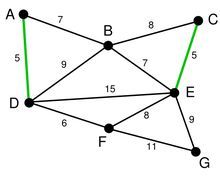
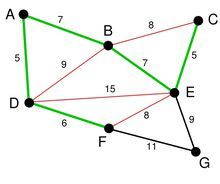
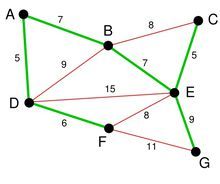
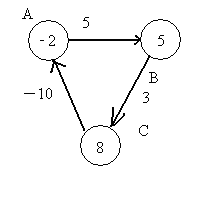
考虑如下的图:
经过第一次遍历后,点B的值变为5,点C的值变为8,这时,注意权重为-10的边,这条边的存在,导致点A的值变为-2。(8+ -10=-2)
第二次遍历后,点B的值变为3,点C变为6,点A变为-4。正是因为有一条负边在回路中,导致每次遍历后,各个点的值不断变小。
在回过来看一下bellman-ford算法的第三部分,遍历所有边,检查是否存在d(v) > d (u) + w(u,v)。因为第二部分循环的次数是定长的,所以如果存在无法收敛的情况,则肯定能够在第三部分中检查出来。比如
此时,点A的值为-2,点B的值为5,边AB的权重为5,5 > -2 + 5. 检查出来这条边没有收敛。
所以,Bellman-Ford算法可以解决图中有权为负数的边的单源最短路径问题。
有向无回路图中的单源最短路径
Dag-shortest-paths(G,w,s)
{
topological sort the vertices of G
Initialize-single-source(G,s)
for each vertex u,taken in topologically sorted order
do for each vertex v ∈Adj[u]
do Relax(u,v,w)
}
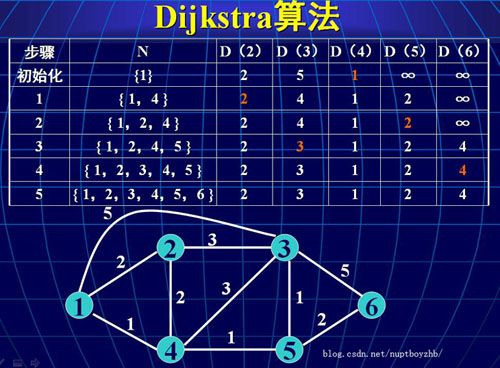
Dijkstra 算法
解决有向图G=(V,E)上带权的单源最短路径问题,但要求所有边的权值非负。
Dijkstra(G,w,s)
{
Initialize-single-source(G,s)
S = Nil
Q = V[G]
while Q != Nil
do u = Extract-min(Q)
S = S∪{u}
for each vertex v ∈Adj[u]
do Relax(u,v,w)
}
差分约束与最短路径
线性规划
差分约束系统
约束图
最短路径性质的证明
三角不等式
对最短路径估计的松弛效果
松弛和最短路径树
第二十五章 每对定点间的最短路径(转)
这里介绍三个算法:矩阵乘法,Floyd-Warshall, Johnson
一:
这个算法和矩阵乘法是很相近的,策略是动态规划,优化子结构是:

其中的L(i,j)m表示的是节点i到节点j之间存在m条边时的最短路径。
然后先给出一个加一条边时的扩展算法:
code:
EXTEND-SHORTEST-PATHS(L, W)
1 n ← rows[L]
2 let be an n × n matrix
3 for i ← 1 to n
4 do for j ← to n
5 do
6 for k ← 1 to n
7 do ![]()
8 return L′
从这里可以看到,每一次加入一条边的时候,我们并不知道加入的边在哪儿,所以k从1到n一直试探,最终选取能导致最小权值的边。
最后,就可以给出这个算法了:
code:
SLOW-ALL-PAIRS-SHORTEST-PATHS(W)
1 n ← rows[W]
2 L(1) W
3 for m ← 2 to n - 1
4 do L(m) ← EXTEND-SHORTEST-PATHS(L(m-1), W)
5 return L(n-1)
示意图:
思想很简答,边数为一的时候,初始化矩阵为权值矩阵。然后边数从2到n-1开始迭代,每次代表的是加入一条边后的矩阵。这里的细节是,生成的矩阵并非是必须要有m条边,而是一个upper-bound,上界,即不大于m条边就行了。n-1的原因是简单路径的边最多是n-1条。
该算法很明显,时间复杂度为O(N4),还不如是对每一个定点作单源呢。所以说,这个算法是可以有改进的。
既然这个算法题目是矩阵乘法,那么它就应该和矩阵乘法有很大的关联。在扩展算法中,我们可以有这样一个变换:
l(m-1) → a,
w → b,
l(m) → c,
min → +,
+ → ·
变换之后,你就发现了,这个扩展算法就是两个矩阵的乘法了:
L(1) = L(0) · W = W,
L(2) = L(1) · W = W2,
L(3) = L(2) · W = W3,
⋮
L(n-1) = L(n-2) · W = Wn-1.
于是,改进思想:
L(1) = W,
L(2) = W2 = W · W,
L(4) = W4 = W2 · W2
L(8) = W8 = W4 · W4
然后得到:
code:
FASTER-ALL-PAIRS-SHORTEST-PATHS(W)
1 n ← rows[W]
2 L(1) ← W
3 m ← 1
4 while m < n - 1
5 do L(2m) ← EXTEND-SHORTEST-PATHS(L(m), L(m))
6 m ← 2m
7 return L(m)
这里没有依次迭代了,而是2的指数次的迭代,时间复杂度降到了O(N3lgN).
虽然这个算法已经有所改进了,但是,我在实践中,还没有用到过该算法。呵呵,只是我自己不喜欢而已。
二,Floyd-Warshall算法
弗洛伊德出算法了,呵呵
这个算法不论从理解,还是从实现上面,都是高人一筹的.
优化子结构:
code:
FLOYD-WARSHALL(W)
1 n ← rows[W]
2 D(0) ← W
3 for k ← 1 to n
4 do for i ← 1 to n
5 do for j ← 1 to n
6 do ![]()
7 return D(n)
示意图:

其中的第二列矩阵是存储的是前驱节点矩阵,以后如果需要生成最短路径时有用。
简单吧,呵呵。概算发的思想不是按照边的条数来动态规划,而是按照两点之间间隔的点来进行动态规划的。
代码中的k代表的是当前路径中的中间节点,不大于k。
这个算法的时间复杂度是O(N3),中间减少了一个N,主要减少就是每次对矩阵进行更新的时候,他是知道当前我要选取的边是那条边,而不像上面的那个算法一样需要从1到n进行扫面进行选取。这有点像01背包问题,要么你要我,然后计算出一个值,如果小于不要我的值,则表示,要我会更优化。
对于最短路径的构造,这里与以前有一点点的不同。以前都只是遇到更有的,更新就行了。这里的前驱节点矩阵需要随着该算法一起进行,而且该矩阵也是一个动态规划的过程。
如果选取了k变得更小,则,parent[i,j] = parent[k,j] ,否则不改变。需要记住的是,每一个矩阵元素,代表的是都是前驱节点。
这里可以稍微改造一下,就能形成一个有向图传递闭包问题的求解方法了。可以看到,在Floyd-Warshall中,每一次的最有子结构都是计算了一下,然后去最小值,如果改成![]() ,其中的t表示 i 到 j 间隔顶点小于k的值,初始化为:
,其中的t表示 i 到 j 间隔顶点小于k的值,初始化为: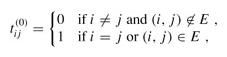
这样每次的计算就变成了一个或运算,很短路很简单。
code:
TRANSITIVE-CLOSURE(G)
1 n ← |V[G]|
2 for i ← 1 to n
3 do for j ← 1 to n
4 do if i = j or (i, j) ∈ E[G]
5 then
6 else
7 for k ← 1 to n
8 do for i ← 1 to n
9 do for j ← 1 to n
10 do
11 return T(n)
示意图:
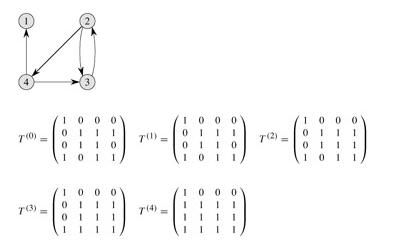
最后还有一种Johnson算法,我这里不想多说了,这个算法在我看来是相当的复杂的,但是他的时间复杂度,在稀疏图中却有着很明显的改善。
给出一些代码:
code:
JOHNSON(G)
1 compute G′, where V[G′] = V[G] ∪ {s},
E[G′] = E[G] ∪ {(s, v) : v ∈ V[G]}, and
w(s, v) = 0 for all v ∈ V[G]
2 if BELLMAN-FORD(G′, w, s) = FALSE
3 then print "the input graph contains a negative-weight cycle"
4 else for each vertex v ∈ V[G′]
5 do set h(v) to the value of δ(s, v)
computed by the Bellman-Ford algorithm
6 for each edge (u, v) ∈ E[G′]
7 do ![]()
8 for each vertex u ∈ V[G]
9 do run DIJKSTRA(G, , u) to compute for all v ∈ V[G]
10 for each vertex v ∈ V[G]
11 do ![]()
12 return D
这个算法是用了两个单源路径算法结合而成的。最开始用到了一个技巧,就是加入了一个定点,并且该定点到其余各点的权值初始化为0,而且没有其他定点能够到达该原点。这一步叫做“重覆权”的方法,目的是让所有的边的权值都为正,而且这还不会改变所有节点之间的最短路径,书上有证明。
最开始用了一个Bellman-Ford算法,判断有没有负权回路,并且顺便计算出加入的定点到其余各点的最短路径。
然后构造出一个没有负权边的图,而且该图的除了新加入的原点之外的原来的所有定点,其最短路径不会发生变化,除了定量的增加一个值之外。
然后对每一个节点,运行dijkstra算法,形成矩阵。
示意图:

Floyd-Warshall算法实现起来比较简单。
第二十六章 最大流(转)
总体上来说,最大流算法分为两大类:增广路 (Augmenting Path) 和预流推进重标号 (Push Relabel) 。也有算法同时借鉴了两者的长处,如 Improved SAP 。本篇主要介绍增广路类算法,思想、复杂度及实际运行效率比较,并试图从中选择一种兼顾代码复杂度和运行效率的较好方案。以下我们将会看到,有时理论分析的时间复杂度并不能很好的反映一种算法的实际效率。
1. Ford - Fulkerson 方法
所有增广路算法的基础都是 Ford - Fulkerson 方法。称之为方法而不是算法是因为 Ford - Fulkerson 只提供了一类思想,在此之上的具体操作可有不同的实现方案。
给定一个有向网络 G(V,E) 以及源点 s 终点 t ,FF 方法描述如下:
Ford-Fulkerson 方法 (G,s,t) 1 将各边上流量 f 初始化为 0 2 while 存在一条增广路径 p 3 do 沿路径 p 增广流量 f 4 return f
假设有向网络 G 中边 (i,j) 的容量为 c(i,j) ,当前流量为 f(i,j) ,则此边的剩余流量即为 r(i,j) = c(i,j) - f(i,j) ,其反向边的剩余流量为 r(j,i) = f(i,j) 。有向网中所有剩余流量 r(i,j) > 0 的边构成残量网络 Gf ,增广路径p即是残量网络中从源点 s 到终点 t 的路径。
沿路径 p 增广流量 f 的操作基本都是相同的,各算法的区别就在于寻找增广路径 p 的方法不同。例如可以寻找从 s 到 t 的最短路径,或者流量最大的路径。
2. Edmonds - Karp 算法
Shortest Augmenting Path (SAP) 是每次寻找最短增广路的一类算法,Edmonds - Karp 算法以及后来著名的 Dinic 算法都属于此。SAP 类算法可统一描述如下:
Shortest Augmenting Path 1 x <-- 0 2 while 在残量网络 Gx 中存在增广路 s ~> t 3 do 找一条最短的增广路径 P 4 delta <-- min{rij:(i,j) 属于 P} 5 沿 P 增广 delta 大小的流量 6 更新残量网络 Gx 7 return x
在无权边的有向图中寻找最短路,最简单的方法就是广度优先搜索 (BFS),E-K 算法就直接来源于此。每次用一遍 BFS 寻找从源点 s 到终点 t 的最短路作为增广路径,然后增广流量 f 并修改残量网络,直到不存在新的增广路径。
E-K 算法的时间复杂度为 O(VE2),由于 BFS 要搜索全部小于最短距离的分支路径之后才能找到终点,因此可以想象频繁的 BFS 效率是比较低的。实践中此算法使用的机会较少。
3. Dinic 算法
BFS 寻找终点太慢,而 DFS 又不能保证找到最短路径。1970年 Dinic 提出一种思想,结合了 BFS 与 DFS 的优势,采用构造分层网络的方法可以较快找到最短增广路,此算法又称为阻塞流算法 (Blocking Flow Algorithm)。
首先定义分层网络 AN(f)。在残量网络中从源点 s 起始进行 BFS,这样每个顶点在 BFS 树中会得到一个距源点 s 的距离 d,如 d(s) = 0,直接从 s 出发可到达的点距离为 1,下一层距离为2 ... 。称所有具有相同距离的顶点位于同一层,在分层网络中,只保留满足条件 d(i) + 1 = d(j) 的边,这样在分层网络中的任意路径就成为到达此顶点的最短路径。
Dinic 算法每次用一遍 BFS 构建分层网络 AN(f),然后在 AN(f) 中一遍 DFS 找到所有到终点 t 的路径增广;之后重新构造 AN(f),若终点 t 不在 AN(f) 中则算法结束。DFS 部分算法可描述如下:
1 p <-- s 2 while s 的出度 > 0 do 3 u <-- p.top 4 if u != t then 5 if u 的出度 > 0 then 6 设 (u,v) 为 AN(f) 中一条边 7 p <-- p, v 8 else 9 从 p 和 AN(f) 中删除点 u 以及和 u 连接的所有边 10 else 11 沿 p 增广 12 令 p.top 为从 s 沿 p 可到达的最后顶点 13 end while
实际代码中不必真的用一个图来存储分层网络,只需保存每个顶点的距离标号并在 DFS 时判断 dist[i] + 1 = dist[j] 即可。Dinic 的时间复杂度为 O(V2E)。由于较少的代码量和不错的运行效率,Dinic 在实践中比较常用。具体代码可参考 DD_engi 网络流算法评测包中的标程,这几天 dinic 算法的实现一共看过和比较过将近 10 个版本了,DD 写的那个在效率上是数一数二的,逻辑上也比较清晰。
4. Improved SAP 算法
本次介绍的重头戏。通常的 SAP 类算法在寻找增广路时总要先进行 BFS,BFS 的最坏情况下复杂度为 O(E),这样使得普通 SAP 类算法最坏情况下时间复杂度达到了 O(VE2)。为了避免这种情况,Ahuja 和 Orlin 在1987年提出了Improved SAP 算法,它充分利用了距离标号的作用,每次发现顶点无出弧时不是像 Dinic 算法那样到最后进行 BFS,而是就地对顶点距离重标号,这样相当于在遍历的同时顺便构建了新的分层网络,每轮寻找之间不必再插入全图的 BFS 操作,极大提高了运行效率。国内一般把这个算法称为 SAP...显然这是不准确的,毕竟从字面意思上来看 E-K 和 Dinic 都属于 SAP,我还是习惯称为 ISAP 或改进的 SAP 算法。
与 Dinic 算法不同,ISAP 中的距离标号是每个顶点到达终点 t 的距离。同样也不需显式构造分层网络,只要保存每个顶点的距离标号即可。程序开始时用一个反向 BFS 初始化所有顶点的距离标号,之后从源点开始,进行如下三种操作:(1)当前顶点 i 为终点时增广 (2) 当前顶点有满足 dist[i] = dist[j] + 1 的出弧时前进 (3) 当前顶点无满足条件的出弧时重标号并回退一步。整个循环当源点 s 的距离标号 dist[s] >= n 时结束。对 i 点的重标号操作可概括为 dist[i] = 1 + min{dist[j] : (i,j)属于残量网络Gf}。具体算法描述如下:
algorithm Improved-Shortest-Augmenting-Path 1 f <-- 0 2 从终点 t 开始进行一遍反向 BFS 求得所有顶点的起始距离标号 d(i) 3 i <-- s 4 while d(s) < n do 5 if i = t then // 找到增广路 6 Augment 7 i <-- s // 从源点 s 开始下次寻找 8 if Gf 包含从 i 出发的一条允许弧 (i,j) 9 then Advance(i) 10 else Retreat(i) // 没有从 i 出发的允许弧则回退 11 return f procedure Advance(i) 1 设 (i,j) 为从 i 出发的一条允许弧 2 pi(j) <-- i // 保存一条反向路径,为回退时准备 3 i <-- j // 前进一步,使 j 成为当前结点 procedure Retreat(i) 1 d(i) <-- 1 + min{d(j):(i,j)属于残量网络Gf} // 称为重标号的操作 2 if i != s 3 then i <-- pi(i) // 回退一步 procedure Augment 1 pi 中记录为当前找到的增广路 P 2 delta <-- min{rij:(i,j)属于P} 3 沿路径 P 增广 delta 的流量 4 更新残量网络 Gf
算法中的允许弧是指在残量网络中满足 dist[i] = dist[j] + 1 的弧。Retreat 过程中若从 i 出发没有弧属于残量网络 Gf 则把顶点距离重标号为 n 。
虽然 ISAP 算法时间复杂度与 Dinic 相同都是 O(V2E),但在实际表现中要好得多。要提的一点是关于 ISAP 的一个所谓 GAP 优化。由于从 s 到 t 的一条最短路径的顶点距离标号单调递减,且相邻顶点标号差严格等于1,因此可以预见如果在当前网络中距离标号为 k (0 <= k < n) 的顶点数为 0,那么可以知道一定不存在一条从 s 到 t 的增广路径,此时可直接跳出主循环。在我的实测中,这个优化是绝对不能少的,一方面可以提高速度,另外可增强 ISAP 算法时间上的稳定性,不然某些情况下 ISAP 会出奇的费时,而且大大慢于 Dinic 算法。相对的,初始的一遍 BFS 却是可有可无,因为 ISAP 可在循环中自动建立起分层网络。实测加不加 BFS 运行时间差只有 5% 左右,代码量可节省 15~20 行。
5. 最大容量路径算法 (Maximum Capacity Path Algorithm)
1972年还是那个 E-K 组合提出的另一种最大流算法。每次寻找增广路径时不找最短路径,而找容量最大的。可以预见,此方法与 SAP 类算法相比可更快逼近最大流,从而降低增广操作的次数。实际算法也很简单,只用把前面 E-K 算法的 BFS 部分替换为一个类 Dijkstra 算法即可。USACO 4.2 节的说明详细介绍了此算法,这里就不详述了。
时间复杂度方面。BFS 是 O(E),简单 Dijkstra 是 O(V2),因此效果可想而知。但提到 Dijkstra 就不能不提那个 Heap 优化,虽然 USACO 的算法例子中没有用 Heap ,我自己还是实现了一个加 Heap 的版本,毕竟 STL 的优先队列太好用了不加白不加啊。效果也是非常明显的,但比起 Dinic 或 ISAP 仍然存在海量差距,这里就不再详细介绍了。
6. Capacity Scaling Algorithm
不知道怎么翻比较好,索性就这么放着吧。叫什么的都有,容量缩放算法、容量变尺度算法等,反正就那个意思。类似于二分查找的思想,寻找增广路时不必非要局限于寻找最大容量,而是找到一个可接受的较大值即可,一方面有效降低寻找增广路时的复杂度,另一方面增广操作次数也不会增加太多。时间复杂度 O(E2logU) 实际效率嘛大约稍好于最前面 BFS 的 E-K 算法,稀疏图时表现较优,但仍然不敌 Dinic 与 ISAP。
7. 算法效率实测!
重头戏之二,虽然引用比较多,哎~
首先引用此篇强文 《Maximum Flow: Augmenting Path Algorithms Comparison》
对以上算法在稀疏图、中等稠密图及稠密图上分别进行了对比测试。直接看结果吧:
稀疏图:
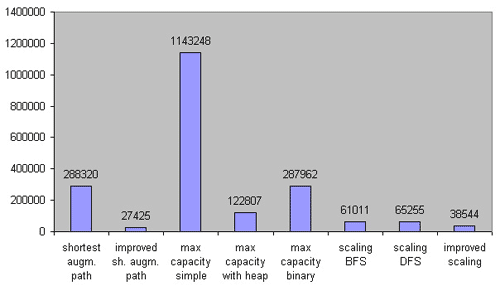
ISAP 轻松拿下第一的位置,图中最左边的 SAP 应该指的是 E-K 算法,这里没有比较 Dinic 算法是个小遗憾吧,他把 Dinic 与 SAP 归为一类了。最大流量路径的简单 Dijkstra 实现实在是太失败了 - -,好在 Heap 优化后还比较能接受……可以看到 Scaling 算法也有不错的表现。
中等稠密图:
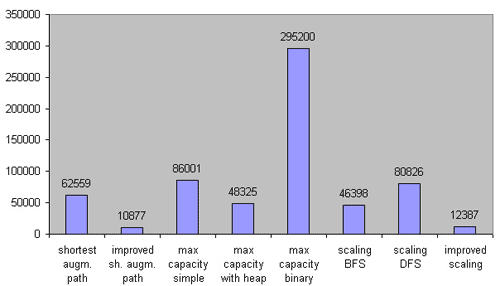
ISAP 依然领先。最大流量算法依然不太好过……几个 Scaling 类算法仍然可接受。
稠密图: