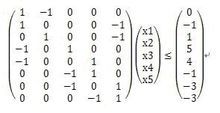POJ 3159 Candies差分约束系统 spfa 附：各种最短路比较

Description

During the kindergarten days, flymouse was the monitor of his class. Occasionally the head-teacher brought the kids of flymouse’s class a large bag of candies and had flymouse distribute them. All the kids loved candies very much and often compared the numbers of candies they got with others. A kid A could had the idea that though it might be the case that another kid B was better than him in some aspect and therefore had a reason for deserving more candies than he did, he should never get a certain number of candies fewer than B did no matter how many candies he actually got, otherwise he would feel dissatisfied and go to the head-teacher to complain about flymouse’s biased distribution.

snoopy shared class with flymouse at that time. flymouse always compared the number of his candies with that of snoopy’s. He wanted to make the difference between the numbers as large as possible while keeping every kid satisfied. Now he had just got another bag of candies from the head-teacher, what was the largest difference he could make out of it?

Input

The input contains a single test cases. The test cases starts with a line with two integers N and M not exceeding 30 000 and 150 000 respectively. N is the number of kids in the class and the kids were numbered 1 through N. snoopy and flymouse were always numbered 1 and N. Then follow M lines each holding three integers A, B and c in order, meaning that kid A believed that kid B should never get over c candies more than he did.

Output

Output one line with only the largest difference desired. The difference is guaranteed to be finite.

Sample Input

2 2
1 2 5
2 1 4

Sample Output

5

Hint

看到这种谁比谁多的情况就应该想到差分约束系统！

啥是差分约束系统？？

如果一个系统由n个变量和m个约束条件组成，其中每个约束条件形如xj-xi<=bk(i,j∈[1,n],k∈[1,m]),则称其为差分约束系统(system of difference constraints)。亦即，差分约束系统是求解关于一组变量的特殊不等式组的方法。

求解差分约束系统，可以转化成图论的 单源最短路径（或最长路径）问题。

观察xj-xi<=bk，会发现它类似最短路中的三角不等式d[v]<=d[u]+w[u,v]，即d[v]-d[u]<=w[u,v]。因此，以每个变量xi为结点，对于约束条件xj-xi<=bk，连接一条边(i,j)，边权为bk。我们再增加一个源点s,s与所有定点相连，边权均为0。对这个图，以s为源点运行Bellman-ford算法（或SPFA算法），最终{d[ i]}即为一组可行解。

例如，考虑这样一个问题，寻找一个5维 向量x=(xi)以满足：

这一问题等价于找出未知量xi，i=1,2,…,5，满足下列8个差分约束条件：

x1-x2≤0

x1-x5≤-1

x2-x5≤1

x3-x1≤5

x4-x1≤4

x4-x3≤-1

x5-x3≤-3

x5-x4≤-3

该问题的一个解为x=(-5,-3,0,-1,-4)，另一个解y=(0,2,5,4,1)，这2个解是有联系的：y中的每个元素比x中相应的元素大5。

而 用spfa算法将x1作为源点S寻找各点的最短路径可以得到这样的值（一般也就是使用spfa算法来解决单源最短路径·差分系统问题）。这也说明，用spfa求源点S到各点的最短路径也就是线性规划问题两点的最大距离，也即是(xs,xi)。如果存在负环回路，那么就不能求出可行解。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=30005;
int dis[maxn],head[maxn];
int n,m,sum;
bool vis[maxn];
struct node{
    int v,w,next;
}edge[150010];
void addedge(int a,int b,int c){
    edge[sum].v=b;
    edge[sum].w=c;
    edge[sum].next=head[a];
    head[a]=sum++;
}
bool spfa(int s){
    int stack[maxn],outque[maxn],top=0;
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    memset(outque,0,sizeof(outque));
    stack[top++]=s;
    vis[s]=1;//vis数组的作用不是判断它是否被更新过 而是是否在栈里！
    dis[s]=0;
    while(top){
        int tmp=stack[--top];
        vis[tmp]=0;
        outque[tmp]++;
        if(outque[tmp]>n)  return 0;  //判断负环，当然这里没有必要写它
        int k=head[tmp];
        while(k>-1){
             if(dis[edge[k].v]>edge[k].w+dis[tmp]){
                  dis[edge[k].v]=edge[k].w+dis[tmp];
                  if(vis[edge[k].v]==0){
                       vis[edge[k].v]=1;
                       stack[top++]=edge[k].v;
                  }
             }
             k=edge[k].next;
        }
    }
    return 1;
}
int main()
{
    //freopen("cin.txt","r",stdin);
    while(cin>>n>>m){
        sum=0;
        memset(head,-1,sizeof(head));
        int a,b,c;
        while(m--){
            scanf("%d%d%d",&a,&b,&c);
            addedge(a,b,c);
        }
        spfa(1);
        printf("%d\n",dis[n]);
    }
    return 0;
}

另：

Dijkstra：适用于权值为非负的图的单源最短路径，用斐波那契堆的复杂度O(E+VlgV)

BellmanFord：适用于权值有负值的图的单源最短路径，并且能够检测负圈，复杂度O(VE)

SPFA：适用于权值有负值，且没有负圈的图的单源最短路径，论文中的复杂度O(kE)，k为每个节点进入Queue的次数，且k一般<=2， 但此处的复杂度证明是有问题的，其实SPFA的最坏情况应该是O(VE).

Floyd：每对节点之间的最短路径。

先给出结论：

(1)当权值为非负时，用Dijkstra。

(2)当权值有负值，且没有负圈，则用SPFA，SPFA能检测负圈，但是不能输出负圈。

(3)当权值有负值，而且可能存在负圈，则用BellmanFord，能够检测并输出负圈。

(4)SPFA检测负环：当存在一个点入队大于等于V次，则有负环，后面有证明。