数值计算模拟的Python和MATLAB实现

作者：金良（[email protected]） csdn博客：http://blog.csdn.net/u012176591

1.数值模拟的意义

数学模型中，往往需要用到数值模拟，一方面是因为想考察模型未来一段时间可能会出现的情况，比如衰减、震荡或混沌等；另一方面，有些微分方程组难以求出解析解，只能求出数值解，这时候也常常用到数值模拟。

2.常微分方程与偏微分方程

凡含有参数，未知函数和未知函数导数 (或微分) 的方程，称为微分方程，有时简称为方程，未知函数是一元函数的微分方程称作常微分方程，未知数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数，称为微分方程的阶。

下面是一个捕食者模型，其中是被捕食者数量，是捕食者数量：

那么描述此模型为：

function xdot=func(t,x)%名称ydot是任取的，func是函数名，也是保存的文件名
r=1;d=0.5;a=0.1;b=0.02;
xdot=[(r-a*x(2))*x(1);
    (-d+b*x(1))*x(2)];

求解函数是ode45()，具体语句：

disp('计算机正在计算中......');
ts = 0:0.1:15;
x0=[25,2];
[t,x] = ode45('func',ts,x0);
plot(t,x),grid,gtext('x(t)'),gtext('y(t)')

参数'func'表示函数文件，ts表示区间，x0表示初始值，t表示返回的时间点向量，x是对应应于t的各个函数的列向量组成的矩阵。

生成的图形如下：

用Python求解：

#encoding=UTF-8
'''
Created on 2014��6��26��

@author: jin
'''
from scipy.integrate import odeint
from pylab import *
def func(x,t):#返回模型的函数
    r=1
    d=0.5
    a=0.1
    b=0.02;
    model = array([(r-a*x[1])*x[0], (-d+b*x[0])*x[1]])
    return model
ts = linspace(0.0,50.0,500)#区间[0,50]，中间均分成500份，也就是每个点距离是50/（500-1）
x0 = array([25,2])#初始值
x = odeint(func,x0,ts)#求解方法
figure()
plot(ts,x[:,0],'--',label='x1')
hold('on')
plot(ts,x[:,1],label='x2')
xlabel('t')
ylabel('x')
legend()
show()

生成的图像如下：

当然我们也可以不使用已有的函数，计算方式如下：

代码如下：

#encoding=UTF-8
'''
Created on 2014��6��26��

@author: jin
'''
from scipy.integrate import odeint
from pylab import *

r=1
d=0.5
a=0.1
b=0.02;
N = 50000
ts = linspace(0.0,50.0,N+1)#区间[0,50]，算上两端一共有501个点，故每个小段的大小是50/（501-1）=0.1
dt = ts[1]-ts[0]
x = [[25],[2]]
for i in range(N):
    temp0 = (r-a*x[1][i])*x[0][i]*dt + x[0][i]
    temp1 = (-d+b*x[0][i])*x[1][i]*dt + x[1][i]
    x[0].append(temp0)
    x[1].append(temp1)
figure()
plot(ts,x[0],'--',label='x1')
hold('on')
plot(ts,x[1],label='x2')
xlabel('t')
ylabel('x')
legend()
show()

截图如下：

可以看到用这种方法计算的结果与使用封装好的函数计算的相同。

但是有一点必须要提到，就是参数N的控制。当N取值过小时，就会严重失真，下图是N取值500时的结果：

3.服从概率分布的数值模拟

以超市的某一收银台为研究对象，顾客到达收银台的时间间隔服从平均时间为10秒的负指数分布。负指数分布为

每个顾客的服务时间服从均值为6.5s，标准差为1.2s的正态分布。

，其中为均值，为标准差。

设第个人到达的时间为，开始接受服务的时刻为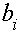，离开时刻为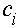。设总共考虑n个顾客。程序首先产生服从均值为10s的负指数分布序列{}，作为n个顾客到达的时间间隔，每个人接受服务时间服从正态分布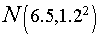的序列{}。则每个人的到达时刻可以采用下列公式进行计算：

第一个顾客接受服务的时刻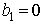，第二个顾客离开的时刻，第i个顾客开始接受服务的时刻为

上面式子的意义是：当第i个顾客到达时间比第 i-1个顾客离开的时间早，则开始接受服务时间为第i-1个顾客离开时间；当 第i个顾客到达时间比第 i-1个顾客离开的时间晚，则开始接受服务时间等于其到达时间。第i个顾客离开时刻为

根据上面的递推公式可以计算出每个人到达的时刻、开始接受服务的时刻和离开的时刻。每个人在收银台逗留时间为，到第n个人离开的时刻为，则系统工作强度（即工作时间）占总时间的比值为

clc;close all;clear all;
disp('计算机大概需要两分钟的运行时间，请等待……');
p=zeros(10,100);avert=zeros(10,100);
%分别在顾客人数为10、100、500等情况时，模拟系统工作强度和顾客平均逗留时间
nn=[10 100 500 1000 5000 10000 20000 50000 100000 500000];
for d=1:10 %length(nn)=10
    for s=1:1000 %每种情况重复模拟100次以便消除随机因素
        n=nn(d);%模拟顾客数目
        dt=exprnd(10,1,n);%到达时间间隔
        st=normrnd(6.5,1.2,1,n);%服务台服务时间
        a=zeros(1,n);%每个顾客到达时刻
        b=zeros(1,n);%每个顾客开始接受服务时刻
        c=zeros(1,n);%每个顾客离开时刻
        a(1)=0;
        for i=2:n
            a(i)=a(i-1)+dt(i-1);%第i顾客到达时刻
            end
        b(1)=0;%第一个顾客开始接受服务的时刻是其到达的时刻
        c(1)=b(1)+st(1);%第一个顾客的离开时刻为其接受的服务时间加上开始接受服务的时刻
           for i=2:n
%如果第i个顾客到达时间比前一个顾客离开时间早，则接受服务时间为前一人离开时间
               if(a(i)<=c(i-1))b(i)=c(i-1);
%如果第i个顾客到达时间比前一个顾客离开时间晚，则接受服务时间为其到达时间
               else b(i)=a(i);
               end
%第i个顾客离开时间为其开始接受服务的时刻+接受服务的时间长度
        c(i)=b(i)+st(i);
           end
        cost=zeros(1,n);%记录每个顾客在系统逗留时间
        for i=1:n
            cost(i)=c(i)-a(i);%第i个顾客在系统逗留时间
        end
        T=c(n);%总时间
        p(d,s)=sum(st)/T;
        avert(d,s)=sum(cost)/n;
    end
end
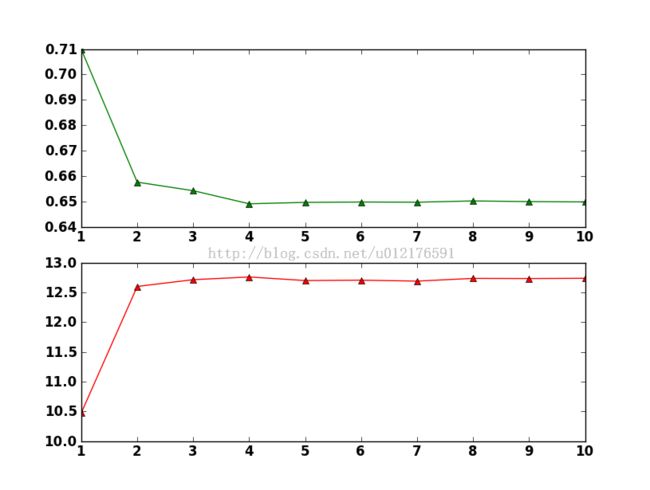
pc=sum(p')/100;avertc=sum(avert')/100;
figure(1);subplot(2,1,1);%分区画图
plot(pc,'color','g','linestyle','-','linewidth',2.5,'marker','*','markersize',5);
text(1,pc(:,1),texlabel('10人'),'fontsize',11);
text(2,pc(:,2),texlabel('10^2 人'),'fontsize',11);
text(3-0.15,pc(:,3)-0.004,texlabel('5x10^2 人'),'fontsize',11);
text(4-0.15,pc(:,4)-0.004,texlabel('10^3 人'),'fontsize',11);
text(5-0.15,pc(:,5)-0.004,texlabel('5x10^3 人'),'fontsize',11);
text(6-0.15,pc(:,6)-0.004,texlabel('10^4 人'),'fontsize',11);
text(7-0.15,pc(:,7)-0.004,texlabel('2x10^4 人'),'fontsize',11);
text(8-0.15,pc(:,8)-0.004,texlabel('5x10^4 人'),'fontsize',11);
text(9-0.15,pc(:,9)-0.004,texlabel('10^5 人'),'fontsize',11);
text(10-0.15,pc(:,10)-0.004,texlabel('5x10^5 人'),'fontsize',11);
xlim([1 11]);xlabel('顾客数量/个','fontsize',11);ylabel('系统工作强度','fontsize',11);
subplot(2,1,2);
plot(avertc,'color','r','linestyle','-','linewidth',2.5,'marker','s','markersize',5);
text(1,avertc(:,1)+0.4,texlabel('10人'),'fontsize',11);
text(2-0.15,avertc(:,2)-0.4,texlabel('10^2 人'),'fontsize',11);
text(3-0.15,avertc(:,3)-0.4,texlabel('5x10^2 人'),'fontsize',11);
text(4-0.15,avertc(:,4)-0.4,texlabel('10^3 人'),'fontsize',11);
text(5-0.15,avertc(:,5)-0.4,texlabel('5x10^3 人'),'fontsize',11);
text(6-0.15,avertc(:,6)-0.4,texlabel('10^4 人'),'fontsize',11);
text(7-0.15,avertc(:,7)-0.4,texlabel('2x10^4 人'),'fontsize',11);
text(8-0.15,avertc(:,8)-0.4,texlabel('5x10^4 人'),'fontsize',11);
text(9-0.15,avertc(:,9)-0.4,texlabel('10^5 人'),'fontsize',11);
text(10-0.15,avertc(:,10)-0.4,texlabel('5x10^5 人'),'fontsize',11);
xlim([1 11]);xlabel('顾客数量/个','fontsize',11);ylabel('顾客逗留时间/秒','fontsize',11);

Python实现：

#encoding=UTF-8

from pylab import * 
import random

N = 100
print u'计算机运行大约需要两分钟的运行时间，请等待。。。。。。'
nn = [10,100,500,1000,5000,10000,20000,50000,100000,500000]
p = tile(0.0,[10,100])#必须为小数，假设为0，则在后边将始终取整数
avert = tile(0.0,[10,100])
for d in range(len(nn)):
    print d
    for s in range(N):
        n = nn[d]
        dt = []     #到达时间间隔
        st = []     #服务时间
        for i in range(nn[d]):
            dt.append(random.expovariate(0.1))#均值为1、0.1=10的指数分布
            st.append(random.normalvariate(6.5,1.2))#均值为6.5，标准差是1.2的正态分布
        a = [0.0]*n   #每个顾客到达时刻
        b = [0.0]*n   #每个顾客开始接受服务时刻
        c = [0.0]*n   #每个顾客离开时刻
        a[0] = 0.0
        for i in range(1,n):
            a[i] = a[i-1]+dt[i-1]
        b[0] = 0.0
        c[0] = b[0]+st[0]
        for i in range(1,n):
            if(a[i]<=c[i-1]):
                b[i] = c[i-1]
            else:
                b[i] = a[i]
            c[i] = b[i] + st[i]
        cost = []
        for i in range(n):
            cost.append(c[i] - a[i])
        T = c[n-1]
        p[d][s] = sum(st)/T      
        avert[d][s] = sum(cost)/n
pc = p.sum(1)/N
avertc = avert.sum(1)/N

x=range(1,len(nn)+1)
figure(1) # 创建图表  
ax1 = subplot(211) # 在图表中创建子图1  
ax2 = subplot(212) # 在图表中创建子图2  
sca(ax1)  
plot(x,pc,'g')  
plot(x,pc,'g^')  
#xlim(0,len(d)+1)  
#ylim(0,max(d)*1.2)  
sca(ax2)  
plot(x,avertc,'r')  
plot(x,avertc,'r^')  
#xlim(0,len(D)+1)  
#ylim(0,max(D)*1.2)  
show()

截图：