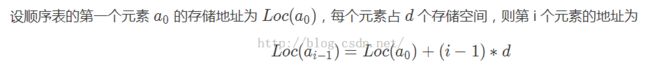重学数据结构系列之——线性表基础
学习来源:计蒜客
顺序表
1.定义
顺序表是在计算机内存中以数组的形式保存的线性表,是指用一组地址连续的存储单元依次存储数据元素的线性结构。线性表采用顺序存储的方式存储就称之为顺序表。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。------by百度百科
最重要的一点,它在内存中是连续的
下面的图和文字解释是从计蒜客复制过来的![]()
顺序表在程序中通常用一维数组实现,一维数组可以是静态分配的,也可以是动态分配的。
在静态分配时,由于数组的大小和空间是固定的,一旦空间占满,就无法再新增数据,否则会导致数据溢出。
而在动态分配时,存储数组的空间在程序执行过程中会动态调整大小,当空间占满时,可以另行开辟更大的存储空间来储存数据。
顺序表最主要的特点是可以进行 随机访问,即可以通过表头元素的地址和元素的编号(下标),在 O(1) 的时间复杂度内找到指定的元素。
顺序表的不足之处是插入和删除操作需要移动大量的元素,从而保持逻辑上和物理上的连续性。
2.顺序表的实现,插入,扩容,查找,删除,遍历
//包含输入输出流库和应该就是字符串的库
#include "iostream"
#include "cstring"
using namespace std;
class Vector{
private:
//size:最大容量,length:当前顺序表的个数
int size, length;
//我们要使用的方式是动态分配,所以就定义个指针
int *data;
public:
//构造函数,input_size:顺序表最大容量
Vector(int input_size){
//初始化最大容量和长度,以及将指向储存元素值的空间的指针初始化
size = input_size;
length = 0;
data = new int[size];
}
//析构函数
~Vector(){
//方括号的存在会使编译器获取数组大小(size)然后析构函数再被依次应用在每个元素上,一共size次。
//因为你申请的数组,这样做也有对称美
delete[] data;
}
//loc:插入位置,value:插入的值
bool insert(int loc, int value){
//先判断插入位置是否合法
if(loc < 0 || loc > length){
return false;
}
//是否达到最大容量了
if(length >= size){
//return false;
//扩容
expand();
}
//从最后一个开始,前一个的值覆盖后一个,直到最后一次,i=loc+1,data[loc+1]=data[loc]
//这样就完成了数据向后移动
for (int i = length; i > loc; i--){
data[i] = data[i-1];
}
//赋值,长度+1
data[loc] = value;
length++;
return true;
}
//扩容
void expand(){
//定义一个指针指向data首地址
int* old_data = data;
//扩大为原来两倍
size = size * 2;
data = new int[size];
//拷贝(复制)数据
for (int i = 0; i < length; i++){
data[i] = old_data[i];
}
//释放原来的空间
delete[] old_data;
}
//查找
int search(int value){
//循环遍历,找到返回索引,否则返回-1
for (int i = 0; i < length; i++){
if (data[i] == value){
return i;
}
}
return -1;
}
//删除
bool remove(int index){
//判断是否越界
if (index < 0 || index >= length) {
return false;
}
//后面覆盖前面的
for (int i = index+1; i< length; i++){
data[i-1] = data[i];
}
//长度-1
length--;
return true;
}
//遍历输出
void print(){
for (int i = 0; i < length; i++) {
//如果不是第一个就先输出一个空格
if (i > 0) {
cout<<" ";
}
cout<<data[i];
}
//最后输出换行
cout<<endl;
}
};
int main(){
Vector a(2);
cout << a.insert(0, 1) << endl;
cout << a.insert(0, 2) << endl;
a.print();
cout << a.remove(1) << endl;
a.print();
cout << a.insert(1, 4) << endl;
cout << a.search(4) << endl;
return 0;
}
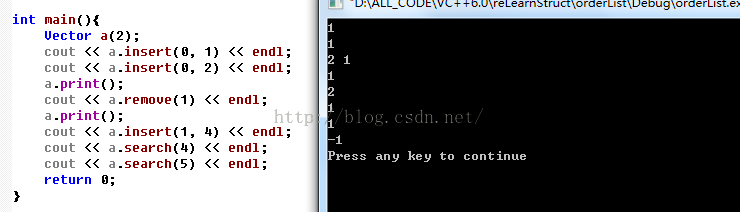
3.运行结果:
解释:插入成功返回true,输出来就被转成1了,同样remove和search也是一样的,search失败返回-1,输出就是-1
4.顺序表的循环左移
循环左移的函数在类的最后一个函数
#include <iostream>
#include <cstring>
using namespace std;
class Vector {
private:
int size, length;
int *data;
public:
Vector(int input_size) {
size = input_size;
length = 0;
data = new int[size];
}
~Vector() {
delete[] data;
}
bool insert(int loc, int value) {
if (loc < 0 || loc > length) {
return false;
}
if (length >= size) {
return false;
}
for (int i = length; i > loc; --i) {
data[i] = data[i - 1];
}
data[loc] = value;
length++;
return true;
}
int search(int value) {
for (int i = 0; i < length; ++i) {
if (data[i] == value) {
return i;
}
}
return -1;
}
bool remove(int index) {
if (index < 0 || index >= length) {
return false;
}
for (int i = index + 1; i < length; ++i) {
data[i - 1] = data[i];
}
length = length - 1;
return true;
}
void print() {
for (int i = 0; i < length; i++) {
if (i > 0) {
cout<<" ";
}
cout<<data[i];
}
//cout<<endl;
}
//循环左移代码,size为你输入数据的个数,count为左移的多少位
void leftShift(int size, int count){
int* tmp = new int[size];
for (int i = 0; i < length; ++i) {
tmp[i] = data[i];
}
for (int i = 0; i < size; i++) {
data[i] = tmp[(i+count)%size];
}
delete[] tmp;
}
};
int main() {
int size,count,tmp;
cin>>size>>count;
if(count<0 || count>size){
return 1;
}
Vector a(size);
for (int i = 0; i < size; i++) {
cin>>tmp;
if(tmp<0 || tmp >10000){
return 1;
}
a.insert(i, tmp);
}
a.leftShift(size, count);
a.print();
return 0;
}
链表
1.定义
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
我要说:指针他也是变量,他自己也有地址,在那个地址里,它储存的也是地址,那个地址就是就是指针的指向,那个地址是个某个结点的地址,那么就说这个指针指向那个结点
2.实现单向链表
#include <iostream>
using namespace std;
//这里定义链表的结点
//链表的结点都是有数据域和指针域组成
class Node{
public:
int data; //数据域
Node* next; //指向下一结点,这样不就能连起来了吗
//构造函数
Node(int _data){
data = _data;
next = NULL;
}
};
class LinkList{
private:
Node* head;
public:
//构造函数
LinkList(){
head = NULL;
}
//插入 node:插入的结点,index:要插入第几个结点的位置
void insert(Node* node, int index){
//链表是空的,也就是头指针是空的,直接将插入元素作为头节点,返回
if(head == NULL){
head = node;
return;
}
//插入的位置是链表头
if(index == 0){
//先把要插入的结点的下一个结点指向原来的头节点head
node->next = head;
//再把插入结点更新为头节点
head = node;
return;
}
//对于一般情况,先找到插入(目标index)位置的前一个位置
Node* current_node = head; //指向当前结点,用于遍历结点
int count = 0; //统计遍历的结点数
//循环语句的作用:找到index的前一个位置
//count < index-1,因为count = index - 1就返回false,循环就退出了
//current_node->next:当前结点的下一个结点,比如现在只有三个结点,你的index是5,这不可能插入吧。
//显然循环到第三个结点时current_node->next就等于空,从而退出循环得了,从而下一个if语句他是不满足的
while (current_node->next != NULL && count < index-1) {
//current_node指向下一结点,
current_node = current_node->next;
count++;
}
//判断index是否超出链表长度,因为index大,上面的循环就会因为current_node->next == NULL 而退出,从而count<index-1
if(count == index-1){
//将node节点的下一个指向current_node的下一个结点
node->next = current_node->next;
//current_node的下一个结点指向node
current_node->next = node;
}
}
//遍历输出函数
void output(){
//链表为空,即头指针为空
if (head == NULL) {
return;
}
Node* current_node = head;
while (current_node != NULL) {
//输出当前结点的数据域
cout<<current_node->data<<" ";
//让指针指向下一结点
current_node = current_node->next;
}
cout<<endl;
}
//删除结点的函数
void delete_node(int index){
if (head == NULL) {
return;
}
Node* current_node = head;
int count = 0;
if (index == 0) {
head = head->next;
delete current_node;
return;
}
// 找目标位置的前一位
while (current_node->next != NULL && count < index-1) {
current_node = current_node->next;
count++;
}
//index不能超出长度 而且不能删除最后一个结点的后一位,即current_node的下一个不能为空
if (count == index-1 && current_node->next != NULL) {
Node* delete_node = current_node->next;
current_node->next = delete_node->next;
//等价于 current_node->next = current_node->next->next; delete current_node->next;
delete delete_node;
}
}
//翻转
void reverse(){
//列表为空就不翻
if (head == NULL) {
return;
}
Node *next_node, *current_node;
//current_node初始化为头结点的下一个
current_node = head->next;
head->next = NULL;
while (current_node != NULL) {
//next_node保存当前结点的下一个结点
next_node = current_node->next;
//使current_node指向原头结点, 下一句是将current_node作为头节点,这样这个两的方向就相反了
current_node->next = head;
head = current_node;
//最后让current_node移动到下一结点,继续两两反向
current_node = next_node;
}
}
};
int main(){
LinkList linklist;
for (int i = 1; i <= 10; i++) {
//新建一个结点
Node *node = new Node(i);
//插入位置从0开始哦
linklist.insert(node, i-1);
}
//调用遍历输出函数
linklist.output();
//删除索引值为5的结点,再输出
linklist.delete_node(5);
linklist.output();
linklist.reverse();
linklist.output();
return 0;
}
3.运行结果
链表的种类
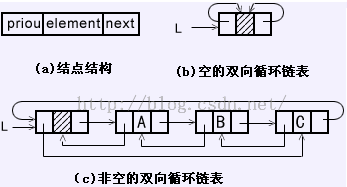
循环链表:就是最后一个结点的指针域指向头节点
双向链表:指针域有两个,一个指向前面的结点,一个指向后面的结点
循环链表解决约瑟夫问题
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int _data) {
data = _data;
next = NULL;
}
};
class LinkList {
private:
Node* head;
public:
LinkList() {
head = NULL;
}
void insert(Node *node, int index) {
if (head == NULL) {
head = node;
//循环链表,只有一个结点时,自己的下一个就是自己
head->next = head;
return;
}
if (index == 0) {
//index==0,node插入成了头,head成了尾,
node->next = head->next; //即node的下一个是原来head的下一个
head->next = node; //head的下一个是node(新的头),这样子的循环就不会断了
return;
}
//即从第一个开始,因为上面head已成尾了
Node *current_node = head->next;
int count = 0;
//current_node如果等于head,就是到尾了,只剩一个元素了,那个就是我们要找的
while (current_node != head && count < index - 1) {
current_node = current_node->next;
count++;
}
if (count == index - 1) {
//我们要插入结点指向 current_node(插入位置的前一个)本来的下一个
node->next = current_node->next;
//current_node(插入位置的前一个)的下一个指向node
current_node->next = node;
}
//如果结点插入到尾结点后面,head(这里当做尾)的后面是node,那么将head指向node
if (node == head->next) {
head = node;
}
}
void output_josephus(int m){
Node* current_node = head;
//若current_node->next等于current_node,就只剩一个结点,就是我们找的,所以要把不等作为循环继续的条件
while (current_node->next != current_node) {
//数到第m-1个就退出,那个元素是我们要删除元素的前一个元素
for (int i = 1; i < m; i++) {
current_node = current_node->next;
}
//输出要删除元素的数据域
cout<<current_node->next->data<<" ";
//用delete_node保存要删除的结点,以便释放其内存
Node* delete_node = current_node->next;
//这个是删除结点的操作
current_node->next = current_node->next->next;
delete delete_node;
}
cout<<endl<<endl;
//输出我们要找的那个,即删剩的最后一个
cout<<current_node->data<<endl;
delete current_node;
}
};
int main() {
LinkList linklist;
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
Node *node = new Node(i);
linklist.insert(node, i - 1);
}
linklist.output_josephus(m);
return 0;
}