数据库系统——B+树索引
原文来自于:http://dblab.cs.toronto.edu/courses/443/2013/05.btree-index.html
1. B+树索引概述
在上一篇文章中,我们讨论了关于index的几个中重要的课题:
A) index是保存在磁盘上的一种数据结构,用于提高查询或是扫描record的速度。
B) 排序索引树通过保存page的指针加速record的查找。(ISAM)
C) 维护排序索引树的代价很高,因此,ISAM通过创建overflow page来解决这个问题,但是过多的overflow page会使查询性能从log(指数log)级别降低到线性遍历。
下面我们将介绍一种高度健壮的、比较流行的一种数据结构——B+树,作为ISAM的扩展。
一般说来,B+树是一种高效的基于磁盘保存的数据结构,主要保存(key, value)pair。它支持对key的高效查找,和高效的范围迭代。
B+树提供了这些功能:
A) 快速的record查找
B) 快速的record遍历
C) 不通过overflow page的形式维护排序树结构
B+树背后的关键思想是利用有序平衡树,替代ISAM中的排序树。
2. B+树的定义
B+树是用磁盘上的page作为node节点的树。B+树中的节点可以区分为leaf node(叶子节点)和interior node(内部节点)。
由于每一个node刚好是磁盘中的一个page,在B+树中,我们使用的术语node和page是可以互换的。
2.1 leaf node
leaf node保存数据entry(条目,相当于record),entry的形式是(key, value)。所有的leaf node也被组织成page链表的形式。B+树的leaf node如下图所示:
下面是leaf node抽象的数据结构定义:
struct LeafNode
{
vector<Key> keys;
vector<Value> values;
PagePointer next_page;
};
对任意的leaf node,下面的公式都是成立的:
p.keys.size() == p.values.size()
2.2 interior node
Interior node组织成一个树的形式,从root node(根节点,根节点也是一个interior node)开始,通过保存一系列key,来加速查询leaf node。
Interior node保存着一系列key和page指针,它的结构如图所示:
下面是interior node抽象的数据结构定义:
struct InteriorNode
{
vector<Key> keys;
vector<PagePointer> pointers;
};
对任意的interior node来时,下面的公式都是成立的:
p.keys.size() +1 == p.pointers.size()
有一个定义:Neighbouring pointer(临近指针)
对于一个key ki,我们定义before(ki)是ki前面临近的page指针,after(ki)是ki后面临近的指针。也就是说:
p.before(ki) = p.pointers[i]
p.after(ki) = p.pointers[i+1]
2.3 B+树的属性和约束条件
2.3.1 node中的key都是排好序的。
假设,p是B+树中的node,那么我们必须维持p.keys关于value是有序的。
2.3.2 各个node之间也是按key进行排序的。
B+树是有序树,表现在一下几个方面:
A) leaf node是有序的:
∀p∈LeafNode,∀k∈p.keys,∀k′∈p.next_page.keys,k<k′
多个leaf node组成一个有序链表,在各个leaf node之间使得高效的对(key, value)遍历成为可能。
B) interior node是有序的:
B+树对所有的key k,和其临近的指针after(k) 、after(k),满足下面的条件:
k>max(keys(before(k)))
k≤min(keys(after(k)))
换句话说,k是介于before(k)、after(k) 的key之间的key。如图:
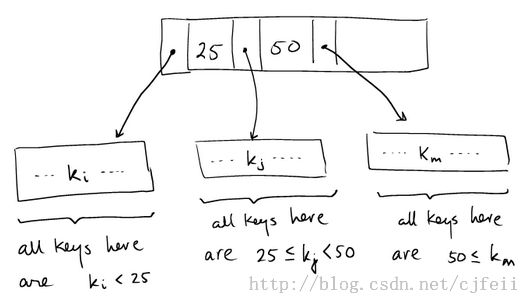
2.3.3 B+树是平衡树
B+树是平衡树,所有从root node到任何leaf node的路径长度是相等的。
2.3.4 B+树node是充分填充的
B+树允许它的node部分填充。主要是设计了一个填充因子的参数,用来限定每个non-root node(非根节点)的最小填充度。
如果一个non-root node的填充度不够,我们就说该node underflow,在B+树里只有root node可以underflow。
这里有一个不合格的B+数的例子。假设我们定义了下面的参数:
Capacity of each node: 4 keys
Fill factor: 50%
当该树经过平衡和排序后,它的结构如下图所示:
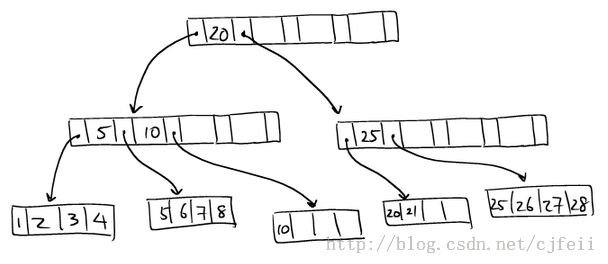
它存在着这样一个问题:没有满足我们上面定义的填充因子(fill factor)50%:
3. B+树的查询search和插入insert
B+树的主要操作有:
/** * finds the leaf node that _should_ contain the entry with the specified key */ LeafNode search(Node root, Key key) /** * Inserts a key/val pair into the tree. * Returns the root of the new tree which _may_ be different * from the old root node. */ InteriorNode insert_into_tree(InteriorNode root, Key newkey, Value val)
B+树的insert算法必须保证执行相应的操作之后使得树依然满足B+的所有属性和约束。
3.1 Searching
B+树的查询算法就是简单直接的树的查找算法:
LeafNode search(Node p, Key key)
{
if(p is LeafNode)
return root;
else
{
if(key < p.keys[0])
return search(before(p.keys[0]), key);
else if(key > p.keys[-1])
return search(after(p.keys[-1]), key);
else {
let i be p.keys[i] <= key < p.keys[i+1]
return search(after(p.keys[i]), key)
}
}
}
3.2 Inserting
B+树的insert操作是非常棘手的。它不像AVL的insert操作那样简单,B+树还需要考虑node的overflow和underflow。
Insert算法从这开始:
1) 寻找insert的正确的目标leaf node
2) 向目标leaf node中尝试insert操作
InteriorNode insert_into_tree(InteriorNode root, Key newkey, Value val)
{
LeafNode leaf = search(root, newkey);
return insert_into_node(leaf, newkey, val);
}
其中,insert_into_node中,要做如下的一些事:
/**
* Tries to inserts the (newkey/val) pair into
* the node.
*
* If `target` is an interior node, then `val` must be a page pointer.
*/
InteriorNode insert_into_node(Node target, newkey, val)
{
if( ... CASE 1 ... )
{
/* handle CASE 1 */
}
else if( ... CASE 2 ... )
{
/* handle CASE 2 */
}
else if( ... CASE 3 ... )
{
/* handle CASE 2 */
}
}
其中三个不同的case包括:
A) 目标leaf node有足够的空间保存key
B) 目标leaf node已满,但是它的parent node(父节点)有足够的空间保存key
C) 目标leaf node和它的parent node已满。
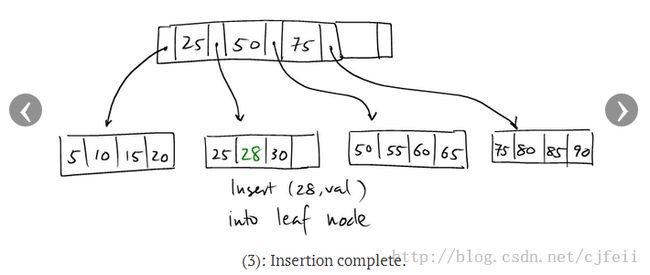
Case 1:
这是最简单的一种情况,将entry(newkey, value) 插入到目标leaf node即可。
A) Root node 不需要改变
B) 磁盘I/O也无需讨论。所有的操作都在一个page中。buffer manager(缓存管理)可以被用到,仿佛所有的node都保存在内存。
如图示:
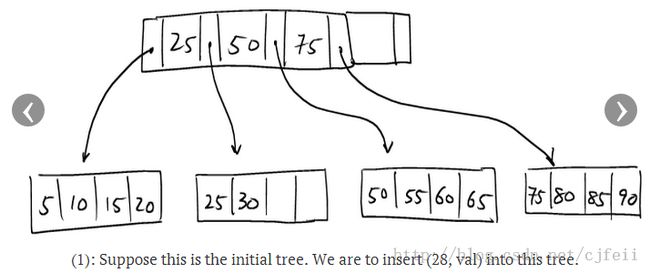
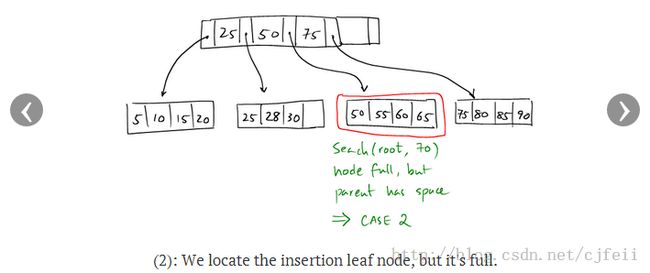
Case 2:
在这种情况下,target node已满,但是它的parent node有足够的空间保存一个key。
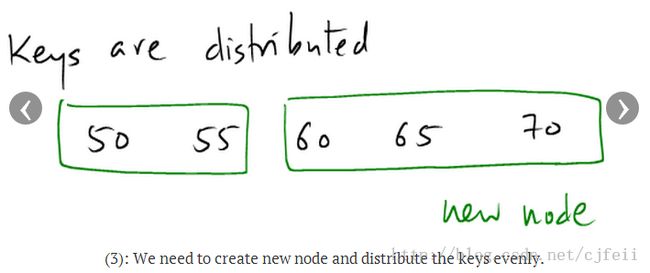
A) 创建一个target node的兄弟node作为new_target node,将new_target node插入带target node之后。
B) 将target node中的所有entry和我们需要增加的entry分配保存到target node和new_target node中。由于分配之前target node是满的,那么就可以断定分配之后,这两个node不会存在underflow。
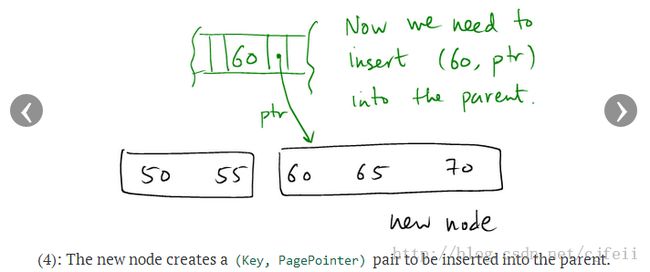
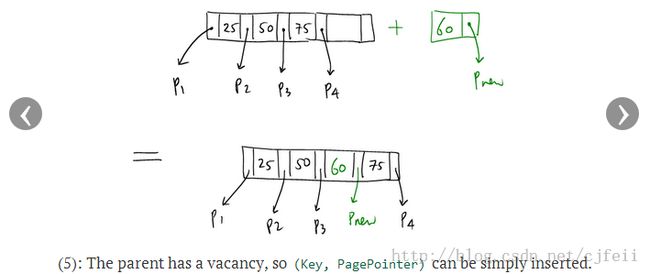
C) 将new_target的指针(k,p) = (leaf2.keys[0], ADDRESS[leaf2]) insert到target node的parent node中。由于parent node有足够的空间保存一个key,所以parent node不会出现overflow。
如图示:

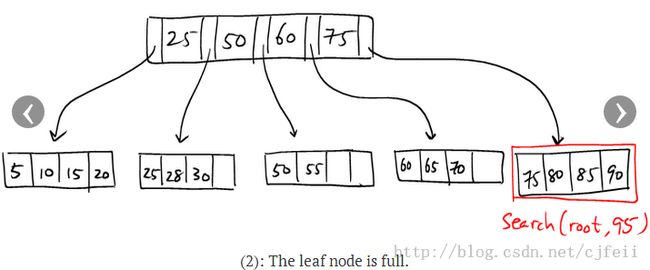
Case 3:
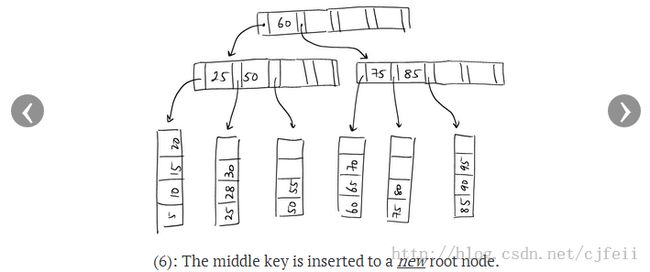
这种情况是target和parent[target]都满了的情况。我们需要递归的尝试将新的key insert到target的祖先node中。甚至都有这种情况:root node也没有足够的空间保存这个新key ,这种情况下,我们必须对root进行分割,创建一个新的node作为B+树的root node。
具体细节如下:
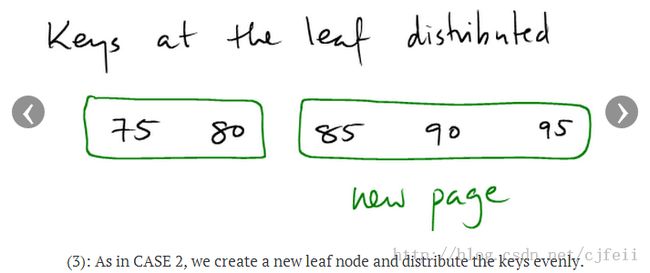
A) 创建一个new_target node,insert到target之后。
B) 将target中的entry分配保存到target和new_target中。
现在我们需要将new_target node的指针(k,p) = (leaf2.keys[0], ADDRESS[leaf2])插入到它的PARENT[target],但是PARENT[target]已经满了。
A) 令target_parent = PARENT[target]
B) 令all_keys = sorted(target_parent.keys ∪ {k})
C) 申请一个新的node:new_interior
D) 令i = floor(all_keys.size() / 2)
middle_key = all_keys[i]
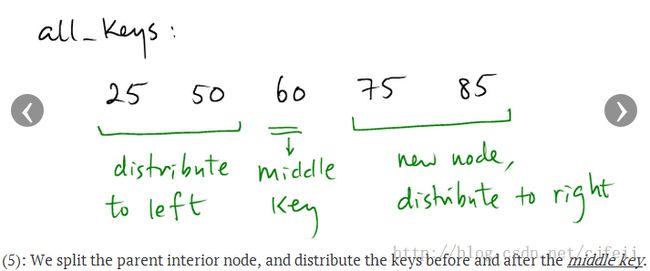
E) 将all_keys[0 .. i-1]保存到target_parent中,将all_keys[i+1 .. n]保存new_interior到中。
F) 如果target_parent是root,那么我们就创建一个新的node作为grandparent ,令grandparent = PARENT[target_parent]。
G) 递归地调用:
insert_into_node(grandparent, middle_key, ADDRESS[new_interior])
如图所示:
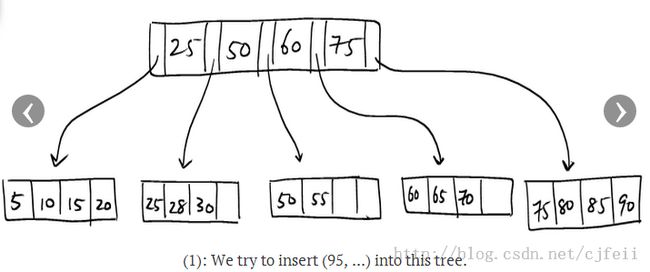
4. B+树的其它的东西
a) B+树也支持高效的删除delete。删除算法是insert算法的逆过程。在delete的算法中会通过merge(合并)node,去避免underflow。如果发生merge node,那么会在parent node递归的delete这个(Key, PagePointer)。
b) 如果所有的data entry都保存在sequential file中,并且关于key排序,那么就可以非常有效的将sequential file装载到B+树。
c) B+树可以作为基于磁盘有序存储的排序算法。