BP算法浅谈（Error Back-propagation）

最近在打基础，大致都和向量有关，从比较基础的人工智能常用算法开始，以下是对BP算法研究的一个小节。

      本文只是自我思路的整理，其中举了个例子，已经对一些难懂的地方做了解释，有兴趣恰好学到人工智能对这块不能深入理解的，可以参考本文。

      

通过带*的权重值重新计算误差，发现误差为0.18，比老误差0.19小，则继续迭代，得神经元的计算结果更加逼近目标值0.5

 

感想

 在一个复杂样本空间下，对输入和输出进行拟合

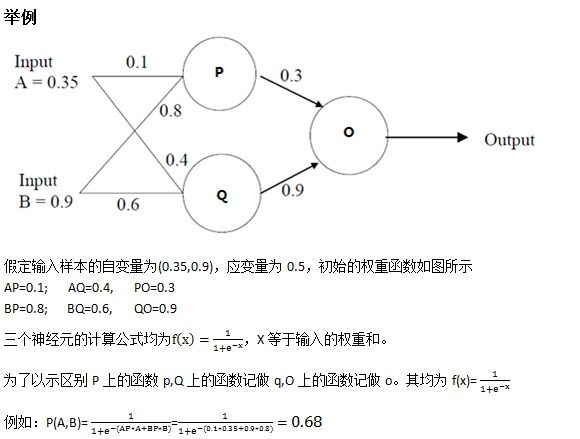
（1）      多少个hidden unit才能符合需要（hidden unit就是图中的P，Q）

（2）      多少层unit才能符合需要（本例为1层）

（3）      如果有n层，每层m个unit，k个输入，1个输出，那么就有K*m^(n+1)条边，每条边有一个权重值，这个计算量非常巨大

（4）      如果k个输入，1个输出，相当于将k维空间，投射到一个1维空间，是否可以提供足够的准确性，如果是k个输入，j个输出，j比k大，是否是一个升维的过程，是否有价值？

 

收获

1）  了解偏导。

2）  了解梯度。

3）  产生新的思考

 

参考文献：

1 http://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)

2 http://www.rgu.ac.uk/files/chapter3%20-%20bp.pdf

3 http://www.cedar.buffalo.edu/~srihari/CSE574/Chap5/Chap5.3-BackProp.pdf

验证代码：

#include "stdio.h"
#include <math.h>
const double e = 2.7182818;
int main(void)
{
        double input[] = {0.35,0.9};
        double matrix_1[2][2]={
                {0.1,0.4},
                {0.8,0.6},
        };
        double matrix_2[] = { 0.3,0.9 };
        for(int s= 0; s<1000; ++s)
        {
                double tmp[] = {0.0,0.0};
                double value = 0.0;
                {
                        for(int i = 0;i<2;++i)
                        {
                                for(int j = 0;j<2;++j)
                                {
                                        tmp[i] += input[j]*matrix_1[j][i];
                                }
                                tmp[i] = 1/(1+pow(e,-1*tmp[i]));
                        }
                        for(int i = 0;i<2;++i)
                        {
                                value += tmp[i]*matrix_2[i];
                        }
                        value = 1/(1+pow(e,-1*value));
                }

              

               double RMSS = (0.5)*( value - 0.5)*(value-0.5);
                printf("%f,%f\n",value,RMSS);

                if(value - 0.5 < 0.01)
                {
                        break;
                }
                double E = value - 0.5;
                matrix_2[0] = matrix_2[0] - E*value*(1-value)*tmp[0];
                matrix_2[1] = matrix_2[1]  - E*value*(1-value)*tmp[1];
                //printf("##%f,%f\n",matrix_2[0],matrix_2[1]);
                matrix_1[0][0] = matrix_1[0][0] - E*value*(1-value)*matrix_2[0]*tmp[0]*(1-tmp[0])*matrix_1[0][0];
                matrix_1[1][0] = matrix_1[1][0] - E*value*(1-value)*matrix_2[0]*tmp[0]*(1-tmp[0])*matrix_1[1][0];

                matrix_1[0][1] = matrix_1[0][1] - E*value*(1-value)*matrix_2[0]*tmp[0]*(1-tmp[1])*matrix_1[0][1];
                matrix_1[1][1] = matrix_1[1][1] - E*value*(1-value)*matrix_2[0]*tmp[0]*(1-tmp[1])*matrix_1[1][1];

                //printf("##%f,%f\n",matrix_1[0][0],matrix_1[1][0]);
                //printf("##%f,%f\n",matrix_1[0][1],matrix_1[1][1]);
        }
        return 0;
}
                       

给出一个带有”增加充量项“BPANN。

有两个输入单元，两个隐藏单元，一个输出单元，三层

# Back-Propagation Neural Networks
#
import math
import random
import string

random.seed(0)

# calculate a random number where:  a <= rand < b
def rand(a, b):
    return (b-a)*random.random() + a

# Make a matrix (we could use NumPy to speed this up)
def makeMatrix(I, J, fill=0.0):
    m = []
    for i in range(I):
        m.append([fill]*J)
    return m

# our sigmoid function, tanh is a little nicer than the standard 1/(1+e^-x)
#使用双正切函数代替logistic函数
def sigmoid(x):
    return math.tanh(x)

# derivative of our sigmoid function, in terms of the output (i.e. y)
# 双正切函数的导数，在求取输出层和隐藏侧的误差项的时候会用到
def dsigmoid(y):
    return 1.0 - y**2

class NN:
    def __init__(self, ni, nh, no):
        # number of input, hidden, and output nodes
        # 输入层，隐藏层，输出层的数量，三层网络
        self.ni = ni + 1 # +1 for bias node
        self.nh = nh
        self.no = no

        # activations for nodes
        self.ai = [1.0]*self.ni
        self.ah = [1.0]*self.nh
        self.ao = [1.0]*self.no
        
        # create weights
        #生成权重矩阵，每一个输入层节点和隐藏层节点都连接
        #每一个隐藏层节点和输出层节点链接
        #大小：self.ni*self.nh
        self.wi = makeMatrix(self.ni, self.nh)
        #大小：self.ni*self.nh
        self.wo = makeMatrix(self.nh, self.no)
        # set them to random vaules
        #生成权重，在-0.2-0.2之间
        for i in range(self.ni):
            for j in range(self.nh):
                self.wi[i][j] = rand(-0.2, 0.2)
        for j in range(self.nh):
            for k in range(self.no):
                self.wo[j][k] = rand(-2.0, 2.0)

        # last change in weights for momentum 
        #?
        self.ci = makeMatrix(self.ni, self.nh)
        self.co = makeMatrix(self.nh, self.no)

    def update(self, inputs):
        if len(inputs) != self.ni-1:
            raise ValueError('wrong number of inputs')

        # input activations
        # 输入的激活函数，就是y=x;
        for i in range(self.ni-1):
            #self.ai[i] = sigmoid(inputs[i])
            self.ai[i] = inputs[i]

        # hidden activations
        #隐藏层的激活函数,求和然后使用压缩函数
        for j in range(self.nh):
            sum = 0.0
            for i in range(self.ni):
                #sum就是《ml》书中的net
                sum = sum + self.ai[i] * self.wi[i][j]
            self.ah[j] = sigmoid(sum)

        # output activations
        #输出的激活函数
        for k in range(self.no):
            sum = 0.0
            for j in range(self.nh):
                sum = sum + self.ah[j] * self.wo[j][k]
            self.ao[k] = sigmoid(sum)

        return self.ao[:]

    #反向传播算法 targets是样本的正确的输出
    def backPropagate(self, targets, N, M):
        if len(targets) != self.no:
            raise ValueError('wrong number of target values')

        # calculate error terms for output
        #计算输出层的误差项 
        output_deltas = [0.0] * self.no
        for k in range(self.no):
            #计算k-o
            error = targets[k]-self.ao[k]
            #计算书中公式4.14
            output_deltas[k] = dsigmoid(self.ao[k]) * error

        # calculate error terms for hidden
        #计算隐藏层的误差项，使用《ml》书中的公式4.15
        hidden_deltas = [0.0] * self.nh
        for j in range(self.nh):
            error = 0.0
            for k in range(self.no):
                error = error + output_deltas[k]*self.wo[j][k]
            hidden_deltas[j] = dsigmoid(self.ah[j]) * error

        # update output weights
        # 更新输出层的权重参数
        # 这里可以看出，本例使用的是带有“增加冲量项”的BPANN
        # 其中，N为学习速率 M为充量项的参数 self.co为冲量项
        # N: learning rate
        # M: momentum factor
        for j in range(self.nh):
            for k in range(self.no):
                change = output_deltas[k]*self.ah[j]
                self.wo[j][k] = self.wo[j][k] + N*change + M*self.co[j][k]
                self.co[j][k] = change
                #print N*change, M*self.co[j][k]

        # update input weights
        #更新输入项的权重参数
        for i in range(self.ni):
            for j in range(self.nh):
                change = hidden_deltas[j]*self.ai[i]
                self.wi[i][j] = self.wi[i][j] + N*change + M*self.ci[i][j]
                self.ci[i][j] = change

        # calculate error
        #计算E(w)
        error = 0.0
        for k in range(len(targets)):
            error = error + 0.5*(targets[k]-self.ao[k])**2
        return error

    #测试函数，用于测试训练效果
    def test(self, patterns):
        for p in patterns:
            print(p[0], '->', self.update(p[0]))

    def weights(self):
        print('Input weights:')
        for i in range(self.ni):
            print(self.wi[i])
        print()
        print('Output weights:')
        for j in range(self.nh):
            print(self.wo[j])

    def train(self, patterns, iterations=1000, N=0.5, M=0.1):
        # N: learning rate
        # M: momentum factor
        for i in range(iterations):
            error = 0.0
            for p in patterns:
                inputs = p[0]
                targets = p[1]
                self.update(inputs)
                error = error + self.backPropagate(targets, N, M)
            if i % 100 == 0:
                print('error %-.5f' % error)


def demo():
    # Teach network XOR function
    pat = [
        [[0,0], [0]],
        [[0,1], [1]],
        [[1,0], [1]],
        [[1,1], [0]]
    ]

    # create a network with two input, two hidden, and one output nodes
    n = NN(2, 2, 1)
    # train it with some patterns
    n.train(pat)
    # test it
    n.test(pat)



if __name__ == '__main__':
    demo()

>>> ================================ RESTART ================================
>>> 
error 0.94250
error 0.04287
error 0.00348
error 0.00164
error 0.00106
error 0.00078
error 0.00125
error 0.00053
error 0.00044
error 0.00038
([0, 0], '->', [0.03668584043139609])
([0, 1], '->', [0.9816625517128087])
([1, 0], '->', [0.9815264813097478])
([1, 1], '->', [-0.03146072993485337])
>>>