hdu3068之manacher算法+详解

最长回文

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5158    Accepted Submission(s): 1755

Problem Description

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度.
回文就是正反读都是一样的字符串,如aba, abba等

 

Input

输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S
两组case之间由空行隔开(该空行不用处理)
字符串长度len <= 110000

 

Output

每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.

 

Sample Input

   
   
   
   

    
    
    
    aaaa

abab
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    4
3
   
   
   
   

manacher算法:

定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长

将字符串s从前扫到后for(int i=0;i<strlen(s);++i)来计算p[i],则最大的p[i]就是最长回文串长度,则问题是如何去求p[i]?

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的

分两种情况:

1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串

然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]

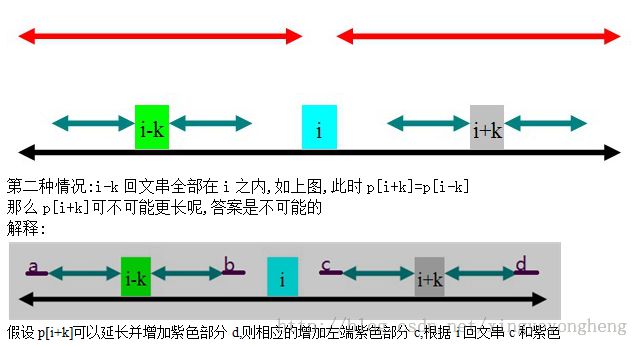
2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k

这样的话p[i+k]就不是从1开始

由于回文串的性质,可知i+k这个位置关于i与i-k对称,

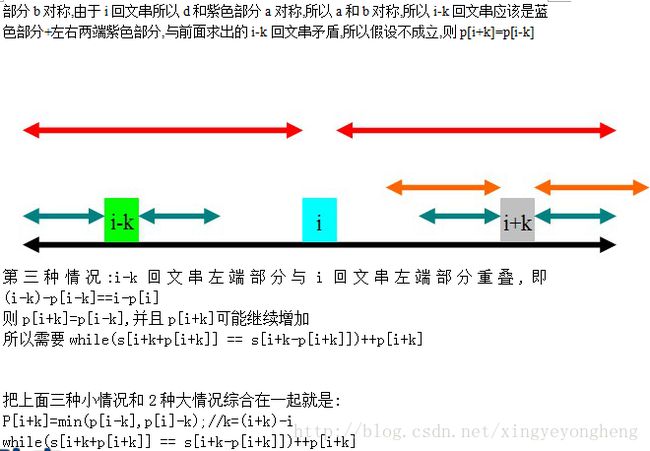
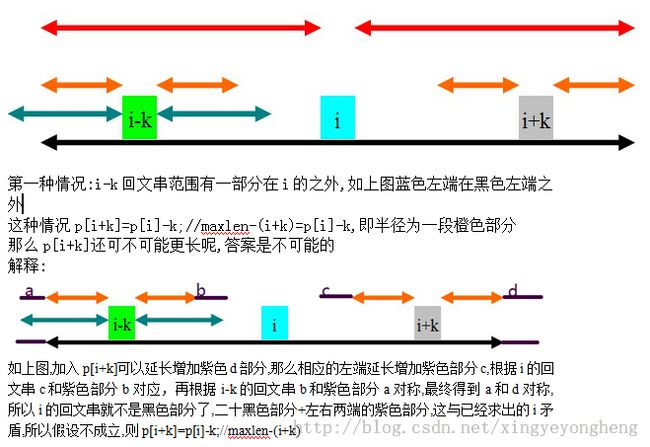
所以p[i+k]分为以下3种情况得出

//黑色是i的回文串范围,蓝色是i-k的回文串范围,

hdu3068代码:

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<string>
 #include<queue>
 #include<algorithm>
 #include<map>
 #include<iomanip>
 #define INF 99999999
 using namespace std;

 const int MAX=110000+10;
 char s[MAX*2];
 int p[MAX*2];

 int main(){
     while(scanf("%s",s)!=EOF){
         int len=strlen(s),id=0,maxlen=0;
         for(int i=len;i>=0;--i){//插入'#'
             s[i+i+2]=s[i];
             s[i+i+1]='#';
         }//插入了len+1个'#',最终的s长度是1~len+len+1即2*len+1,首尾s[0]和s[2*len+2]要插入不同的字符
         s[0]='*';//s[0]='*',s[len+len+2]='\0',防止在while时p[i]越界
         for(int i=2;i<2*len+1;++i){
             if(p[id]+id>i)p[i]=min(p[2*id-i],p[id]+id-i);
             else p[i]=1;
             while(s[i-p[i]] == s[i+p[i]])++p[i];
             if(id+p[id]<i+p[i])id=i;
             if(maxlen<p[i])maxlen=p[i];
         }
         cout<<maxlen-1<<endl;
     }
     return 0;
 }

下面这道也是manacher算法题
http://acm.hdu.edu.cn/showproblem.php?pid=3294