猴年大吉之开心刷题
过年了,各种走亲访友,大吃大喝。为了不让自己忘了算法为何物,做了几道练手的题。
N=4
打表:
nyist 46
最少乘法次数
http://acm.nyist.net/JudgeOnline/problem.php?pid=46
给你一个非零整数,让你求这个数的n次方,每次相乘的结果可以在后面使用,求至少需要多少次乘。如24:2*2=22(第一次乘),22*22=24(第二次乘),所以最少共2次;
分析:实际上那个指数是很大的,题目描述有问题。#include <iostream>
#include <cmath>
#include <cstdio>
using namespace std;
const int N=5e6+10;
int p[N];
void init(){
p[1]=0;
p[2]=1;
for(int i=3;i<N;i++){
if(i&1) p[i]=p[i-1]+1;
else p[i]=p[i/2]+1;
}
}
int main()
{
init();
int t,n;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
printf("%d\n",p[n]);
}
return 0;
}
nyist 1087
摆方格
http://acm.nyist.net/JudgeOnline/problem.php?pid=1087
大意:在N*N的方格中连续摆放数字,求左上至右下对角线的元素和最大值
分析:个人认为,此题不止2这个难度。
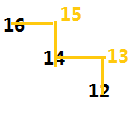
我们知道:小折线走法可以使得和最大。假设N=4,那么,有:

但是不能一直这样走。不然就不能够连续了。
故可以先填充好边界部分,留下小折线路线,最后自然形成最大值。
如:
N=5
| 19 | 20 | 1 | 2 | 3 |
| 18 | 21 | 22 | 5 | 4 |
| 17 | 16 | 23 | 6 | 7 |
| 14 | 15 | 24 | 25 | 8 |
| 13 | 12 | 11 | 10 | 9 |
| 16 | 1 | 2 | 3 |
| 15 | 14 | 13 | 4 |
| 10 | 11 | 12 | 5 |
| 9 | 8 | 7 | 6 |
发现规律:
有
一共N-1项
再加上:
#include <iostream>
#include <cstdio>
using namespace std;
typedef unsigned long long LL;
int main()
{
LL n;
while(cin>>n){
LL ans=(n-1)*n*n-(n-1)*(n-2)+(n*n-2*(n-2))/2;
printf("%llu\n",ans);
}
return 0;
}
nyist 66
分数拆分
http://acm.nyist.net/JudgeOnline/problem.php?pid=66
大意:输入一个正整数k,找到所有的正整数x>=y,使得1/k=1/x+1/y.
分析:做完此题,瞬间感觉到浮点数的强大。
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-7;
int main()
{
int t,k;
cin>>t;
while(t--){
scanf("%d",&k);
for(int y=k+1;y<=2*k;y++){
for(int x=y;;x++){
double p1=1.0/k;
double p2=1.0/x+1.0/y;
if(fabs(p1-p2)<eps) {
printf("1/%d=1/%d+1/%d\n",k,x,y);
}
if(p1-p2>eps) break;
}
}
}
return 0;
}
nyist 743 复杂度
http://acm.nyist.net/JudgeOnline/problem.php?pid=743
问:
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
for(k=j+1;k<=n;k++)
operation;
你知道 operation 共执行了多少次吗
分析:规律题。i<j<k<……<
相当于在N个元素中取M个,这M个元素是递增的。即M个元素一旦选定,就只有一种情况,没有排列的情况。所以:C(n,m)
用素因子做居然Wa了。为什么。。。
WA:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const LL mod=1009,N=2005;
LL pri[N],cnt;
bool vis[N];
void getpri(){
for(LL i=2;i<N;i++){
if(!vis[i]) pri[cnt++]=i;
for(LL j=0;j<cnt&&i*pri[j]<N;j++){
vis[i*pri[j]]=1;
if(i%pri[j]==0) break;
}
}
}
LL getd(LL a,LL d){
LL ans=0;
while(a){
a/=d;
ans=ans+a;
}
return ans;
}
LL power(LL a,LL p){
LL ans=1;
a=a%mod;
while(p>0){
if(p&1) ans=ans*a%mod;
a=a*a%mod;
p>>=1;
}
return ans;
}
int main()
{
getpri();
LL n,m;
while(cin>>m>>n&&(m+n)){
LL ans=1;
for(LL i=0;pri[i]<=n;i++){
LL t1=getd(n,pri[i]),t2=getd(n-m,pri[i]),t3=getd(m,pri[i]);
ans=ans*power(pri[i],t1-t2-t3)%mod;
}
printf("%d\n",ans);
}
return 0;
}
打表:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int mod=1009,N=2005;
int dp[N][N];
void init(){
for(int i=0;i<N;i++){
dp[i][0]=dp[i][i]=1;
}
for(int i=2;i<N;i++){
for(int j=1;j<i;j++){
dp[i][j]=(dp[i-1][j-1]+dp[i-1][j])%mod;
}
}
}
int main()
{
init();
int n,m;
while(cin>>m>>n&&(m+n)){
printf("%d\n",dp[n][m]);
}
return 0;
}