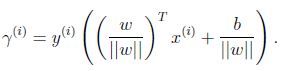SVM(一)
本讲大纲：
1.朴素贝叶斯（Naive Bayes）
2.神经网络（Neural Networks）
3.支持向量机（Support vector machines）
1.朴素贝叶斯
前面讲的主要是是二元值的特征，更一般化的是xi可以取{1，2，3…k}，这样的话可以用多项式分布代替伯努利分布对p(x|y)进行建模. 即使一些输入特征是连续值，我们也很容易离散化. 就比如说我们xi表示居住面积，我们可以离散化如下：
然后我们可以利用朴素贝叶斯算法，用多项式分布进行建模.
当原始的连续值在多项分布中建模效果不是很好时，离散这些特征然后使用朴素贝叶斯（而不是GDA）常常会得到一个更好的结果.
文本分类的事件模型
在文本分类的特定语境下，朴素贝叶斯使用多变量伯努利事件模型（multi-variate Bernoulli event model）.
多项式事件模型（multinomial event model）
为了说明这个模型，换一种记号的方法.
xi表示在一封邮件中的第i个词，xi的取值为
，其中
表示字典的大小. n个词的邮件可以表示为向量
.
假设邮件产生的方式是由垃圾还是非垃圾邮件决定是一个随机的过程，邮件的发送者写的第一个词x1是由服从p(x1|y)的多项式分布产生的，x2是独立与x1的并且来自于同一个多项式分布，同样的，产生x3,x4，一直到xn. 因为所有的这个信息的概率是
.
模型的参数为：
注意p(xj|y)对所有的j来说都是一样的，也就是说词的产生和它的位置无关.
似然性：
参数的最大似然估计为：
应用laplace平滑，分子加1，分母加|V|，得到：
2.神经网络
现在想讨论的问题是非线性分类器（non-linear classifier）.
分类算法中用logistic回归画出一条直线把训练集分开，但是有时候并不能被一条直线分开，我们希望：
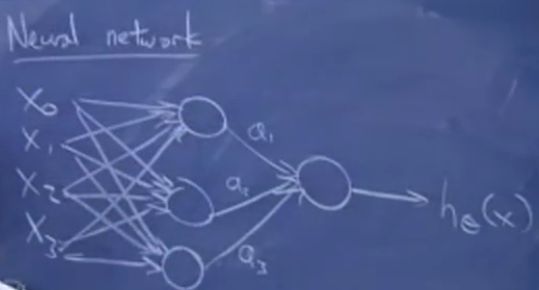
假设特征是x0,x1,x2,x3，圈圈表示计算节点，最后的输出为hθ(x)，得到非线性分界线假设，如图：
输入特征输入到多个sigmoid单元，然后这些单元再输入到一个sigmoid单元，得到神经网络，这些中间节点叫做隐藏层，神经网络可以有多个隐藏层.
其中的参数:
a2,a3都是类似的；
最终的输出，
展示通过神经网络识别数字的程序，即使有很多的噪音效果依旧非常好！
3.支持向量机（SVM）
很多人认为SVM是最好的监督学习算法.
考虑logistic回归：
预测1等价于
等价于
，
越大，就越大，就越高的程度预测1，也就是可以说如果，那么y=1. 类似地，如果那么y=0.
如果能够找到参数使得当y(i)=1时，
，而当y(i)=0时有
. 那么这个预测对训练集很好的.
为了讨论SVM的简单性，介绍一种新的标记：
这里b代替了
的角色，w代替的角色.
函数间隔（functional margin):
如果
，为了使函数间隔很大，
需要是一个很大的正数；相反，如果
为了使函数间隔很大，需要
是一个很大的负数. 如果
，则我们的预测结果是正确的. 因此，一个大的函数间隔表示一个很确定的正确预测.
但是注意到的一个问题是，如果用2w代替w，用2b代替b，那么由于
，不会对
有任何改变，也就是说只是取决于符号而跟数量没有关系. 但是用（2w,2b）代替（w,b）会使得函数间隔间隔增大两倍，似乎不用改变任何有意义的东西函数间隔就可以变得任意大. 直接告诉我们可以正规化(normalization), 可以用
代替(w,b).
定义整个训练集的函数间隔为单个训练样本的最小值，记做：
几何间隔（geometric margins）:
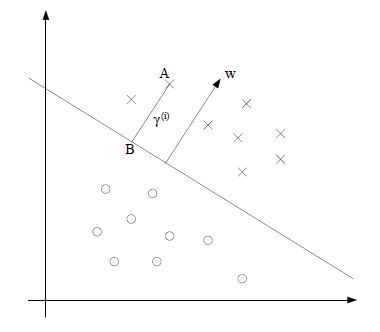
w是垂直分隔超平面的，考虑训练样本A，它到决定边界线的距离是
，也就是线段AB的长度. 
是单位向量（unit-length vector）, B点表示为为：
，在决定边界线上的所有点满足因此：
解到：
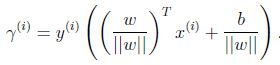
如果||w||等于1，函数间隔等于几何间隔. 几何间隔是不会随着参数的调整而变化的.
定义整个训练集的几何间隔为单个训练样本的几何间隔的最小值：
