Latin方及Hadamard矩阵

Latin方：N个元素在N*N的矩阵中每一行每一列仅仅出现一次。

普通Latin方的构造：

int g[105][105];
void paint(int n){
    for(int i=1;i<=n;i++){
        g[1][i]=i;
    }
    for(int i=2;i<=n;i++){
        for(int j=n;j>1;j--){
            g[i][j]=g[i-1][j-1];
        }
        g[i][1]=g[i-1][n];
    }
}

正交拉丁方：

设 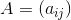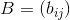， 是两个N阶拉丁方。同一位置上的数字配对后，有序数对全部互异。那么AB正交。

1，2，6阶的拉丁方是没有正交的。

4阶正交阵：

(4.1)(3.3)(2.4)(1.2)

(2.2)(1.4)(4.3)(3.1)

(1.3)(2.1)(3.2)(4.4)

(3.4)(4.2)(1.1)(2.3)

如果，n>=3，n=pa，p是一个素数，a是一个正整数，那么有n-1个正交的拉丁方。

构造：

第i个矩阵：

void paint(int n){
    for(int i=1;i<=n-1;i++){
        cout<<"matrix: "<<i<<endl;
        for(int j=1;j<=n;j++)  cout<<j<<" ";  cout<<endl;
        int last=n;
        for(int ii=2;ii<=n;ii++){
            int first=last+i+1;
            while(first>n) first-=n;  // 避免n变成0
            for(int j=first;j<=n;j++) cout<<j<<" ";
            for(int j=1;j<first;j++) cout<<j<<" ";
            cout<<endl;
            last=first-1;
        }
    }
}

Hadamard矩阵：设矩阵H满足  ，且所有的元素是1或者-1，那么H即是hadamard矩阵。

它的性质（我暂时听说有这三条）：

Hn为正交方阵，所谓正交矩阵指它的任意两行（或两列）都是正交的；

任意一行（列）的所有元素的平方和等于方阵的阶数；

Hadamard矩阵的阶数都是2或者是4的倍数。

递归方法构造（2阶H原始矩阵在1区）：

3区  |  4区

------------

1区  |  2区

（我表示这种构造方法我看的似懂非懂~）

#include <iostream>
#include <cstdio>
using namespace std;
int H[2][2]={
1,1,
1,-1
};
int dfs(int x,int y){
    if(x<2 && y<2) return H[x][y];
    int i=0,j=0;
    if(x>=2){
        i=1;
        while(i*2<=x) i=i<<1;
        x-=i;
    }
    if(y>=2){
        j=1;
        while(j*2<=y) j=j<<1;
        y-=j;
    }
    if(i==j) return -dfs(x,y);  // 4
    else if(i>j) return dfs(x,y+j);  // 3
    else return dfs(x+i,y);  // 2
}
int g[105][105],g2[105][105],g3[105][105];
int main()  // g为hadamard矩阵 g2为其转置  g3为相乘后的结果
{
    int n;
    while(cin>>n){
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g[i][j]=dfs(i,j);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g2[j][i]=g[i][j];
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g3[i][j]=0;
                for(int k=0;k<n;k++){
                    g3[i][j]+=g[i][k]*g2[k][j];
                }
                cout<<g3[i][j]<<" ";
            }
            cout<<endl;
        }
    }
    return 0;
}