视觉SLAM漫谈123456

视觉SLAM漫谈

http://www.cnblogs.com/gaoxiang12/p/3695962.html

1.    前言

　　开始做SLAM（机器人同时定位与建图）研究已经近一年了。从一年级开始对这个方向产生兴趣，到现在为止，也算是对这个领域有了大致的了解。然而越了解，越觉得这个方向难度很大。总体来讲有以下几个原因：

• 入门资料很少。虽然国内也有不少人在做，但这方面现在没有太好的入门教程。《SLAM for dummies》可以算是一篇。中文资料几乎没有。
• SLAM研究已进行了三十多年，从上世纪的九十年代开始。其中又有若干历史分枝和争论，要把握它的走向就很费工夫。
• 难以实现。SLAM是一个完整的系统，由许多个分支模块组成。现在经典的方案是“图像前端，优化后端，闭环检测”的三部曲，很多文献看完了自己实现不出来。
• 自己动手编程需要学习大量的先决知识。首先你要会C和C++，网上很多代码还用了11标准的C++。第二要会用Linux。第三要会cmake，vim/emacs及一些编程工具。第四要会用openCV, PCL, Eigen等第三方库。只有学会了这些东西之后，你才能真正上手编一个SLAM系统。如果你要跑实际机器人，还要会ROS。

　　当然，困难多意味着收获也多，坎坷的道路才能锻炼人（比如说走着走着才发现Linux和C++才是我的真爱之类的。）鉴于目前网上关于视觉SLAM的资料极少，我于是想把自己这一年多的经验与大家分享一下。说的不对的地方请大家批评指正。

　　这篇文章关注视觉SLAM，专指用摄像机，Kinect等深度像机来做导航和探索，且主要关心室内部分。到目前为止，室内的视觉SLAM仍处于研究阶段，远未到实际应用的程度。一方面，编写和使用视觉SLAM需要大量的专业知识，算法的实时性未达到实用要求；另一方面，视觉SLAM生成的地图（多数是点云）还不能用来做机器人的路径规划，需要科研人员进一步的探索和研究。以下，我会介绍SLAM的历史、理论以及实现的方式，且主要介绍视觉（Kinect）的实现方式。

2.    SLAM问题

　　SLAM，全称叫做Simultaneous Localization and Mapping，中文叫做同时定位与建图。啊不行，这么讲下去，这篇文章肯定没有人读，所以我们换一个讲法。

3.    小萝卜的故事

　　从前，有一个机器人叫“小萝卜”。它长着一双乌黑发亮的大眼睛，叫做Kinect。有一天，它被邪恶的科学家关进了一间空屋子，里面放满了杂七杂八的东西。

 

　　小萝卜感到很害怕，因为这个地方他从来没来过，一点儿也不了解。让他感到害怕的主要是三个问题：

　　1.          自己在哪里？

　　2.          这是什么地方？

　　3.          怎么离开这个地方？

　　在SLAM理论中，第一个问题称为定位 (Localization)，第二个称为建图 (Mapping)，第三个则是随后的路径规划。我们希望借助Kinect工具，帮小萝卜解决这个难题。各位同学有什么思路呢？

4.    Kinect数据

　　要打败敌人，首先要了解你的武器。不错，我们先介绍一下Kinect。众所周知这是一款深度相机，你或许还听说过别的牌子，但Kinect的价格便宜，测量范围在3m-12m之间，精度约3cm，较适合于小萝卜这样的室内机器人。它采到的图像是这个样子的（从左往右依次为rgb图，深度图与点云图）：

 

　　Kinect的一大优势在于能比较廉价地获得每个像素的深度值，不管是从时间上还是从经济上来说。OK，有了这些信息，小萝卜事实上可以知道它采集到的图片中，每一个点的3d位置。只要我们事先标定了Kinect，或者采用出厂的标定值。

　　我们把坐标系设成这个样子，这也是openCV中采用的默认坐标系。

 

　　o’-uv是图片坐标系，o-xyz是Kinect的坐标系。假设图片中的点为(u,v)，对应的三维点位置在(x,y,z)，那么它们之间的转换关系是这样的：

 

　　或者更简单的：

 

　　后一个公式给出了计算三维点的方法。先从深度图中读取深度数据（Kinect给的是16位无符号整数），除掉z方向的缩放因子，这样你就把一个整数变到了以米为单位的数据。然后，x,y用上面的公式算出。一点都不难，就是一个中心点位置和一个焦距而已。f代表焦距，c代表中心。如果你没有自己标定你的Kinect，也可以采用默认的值：s=5000, cx = 320, cy=240, fx=fy=525。实际值会有一点偏差，但不会太大。

5.    定位问题

　　知道了Kinect中每个点的位置后，接下来我们要做的，就是根据两帧图像间的差别计算小萝卜的位移。比如下面两张图，后一张是在前一张之后1秒采集到的：

   

　　你肯定可以看出，小萝卜往右转过了一定的角度。但究竟转过多少度呢？这就要靠计算机来求解了。这个问题称为相机相对姿态估计，经典的算法是ICP（Iterative Closest Point，迭代最近点）。这个算法要求知道这两个图像间的一组匹配点，说的通俗点，就是左边图像哪些点和右边是一样的。你当然看见那块黑白相间的板子同时出现在两张图像中。在小萝卜看来，这里牵涉到两个简单的问题：特征点的提取和匹配。

　　如果你熟悉计算机视觉，那你应该听说过SIFT, SURF之类的特征。不错，要解决定位问题，首先要得到两张图像的一个匹配。匹配的基础是图像的特征，下图就是SIFT提取的关键点与匹配结果：

  

　　对实现代码感兴趣的同学请Google“opencv 匹配”即可，在openCV的教程上也有很明白的例子。上面的例子可以看出，我们找到了一些匹配，但其中有些是对的（基本平等的匹配线），有些是错的。这是由于图像中存在周期性出现的纹理（黑白块），所以容易搞错。但这并不是问题，在接下来的处理中我们会将这些影响消去。

　　得到了一组匹配点后，我们就可以计算两个图像间的转换关系，也叫PnP问题。它的模型是这样的：

 

　　R为相机的姿态，C为相机的标定矩阵。R是不断运动的，而C则是随着相机做死的。ICP的模型稍有不同，但原理上也是计算相机的姿态矩阵。原则上，只要有四组匹配点，就可以算这个矩阵。你可以调用openCV的SolvePnPRANSAC函数或者PCL的ICP算法来求解。openCV提供的算法是RANSAC（Random Sample Consensus，随机采样一致性）架构，可以剔除错误匹配。所以代码实际运行时，可以很好地找到匹配点。以下是一个结果的示例。

 

　　上面两张图转过了16.63度，位移几乎没有。

　　有同学会说，那只要不断匹配下去，定位问题不就解决了吗？表面上看来，的确是这样的，只要我们引入一个关键帧的结构（发现位移超过一个固定值时，定义成一个关键帧）。然后，把新的图像与关键帧比较就行了。至于建图，就是把这些关键帧的点云拼起来，看着还有模有样，煞有介事的：

 

1－200帧的匹配结果

　　然而，如果事情真这么简单，SLAM理论就不用那么多人研究三十多年了（它是从上世纪90年代开始研究的）（上面讲的那些东西简直随便哪里找个小硕士就能做出来……）。那么，问题难在什么地方呢？

6.    SLAM端优化理论

　　最麻烦的问题，就是“噪声”。这种渐近式的匹配方式，和那些惯性测量设备一样，存在着累积噪声。因为我们在不断地更新关键帧，把新图像与最近的关键帧比较，从而获得机器人的位移信息。但是你要想到，如果有一个关键帧出现了偏移，那么剩下的位移估计都会多出一个误差。这个误差还会累积，因为后面的估计都基于前面的机器人位置……哇！这后果简直不堪设想啊（例如，你的机器人往右转了30度，再往左转了30度回到原来的位置。然而由于误差，你算成了向右转29度，再向左转31度，这样你构建的地图中，会出现初始位置的两个“重影”）。我们能不能想办法消除这个该死的误差呢？

　　朋友们，这才是SLAM的研究，前面的可以说是“图像前端”的处理方法。我们的解决思路是：如果你和最近的关键帧相比，会导致累计误差。那么，我们最好是和更前面的关键帧相比，而且多比较几个帧，不要只比较一次。

　　我们用数学来描述这个问题。设：

 

　　不要怕，只有借助数学才能把这个问题讲清楚。上面的公式中，xp是机器人小萝卜的位置，我们假定由n个帧组成。xL则是路标，在我们的图像处理过程中就是指SIFT提出来的关键点。如果你做2D SLAM，那么机器人位置就是x, y加一个转角theta。如果是3D SLAM，就是x,y,z加一个四元数姿态（或者rpy姿态）。这个过程叫做参数化（Parameterization）。

　　不管你用哪种参数，后面两个方程你都需要知道。前一个叫运动方程，描述机器人怎样运动。u是机器人的输入，w是噪声。这个方程最简单的形式，就是你能通过什么方式（码盘等）获得两帧间的位移差，那么这个方程就直接是上一帧与u相加即得。另外，你也可以完全不用惯性测量设备，这样我们就只依靠图像设备来估计，这也是可以的。

　　后一个方程叫观测方程，描述那些路标是怎么来的。你在第i帧看到了第j个路标，产生了一个测量值，就是图像中的横纵坐标。最后一项是噪声。偷偷告诉你，这个方程形式上和上一页的那个方程是一模一样的。

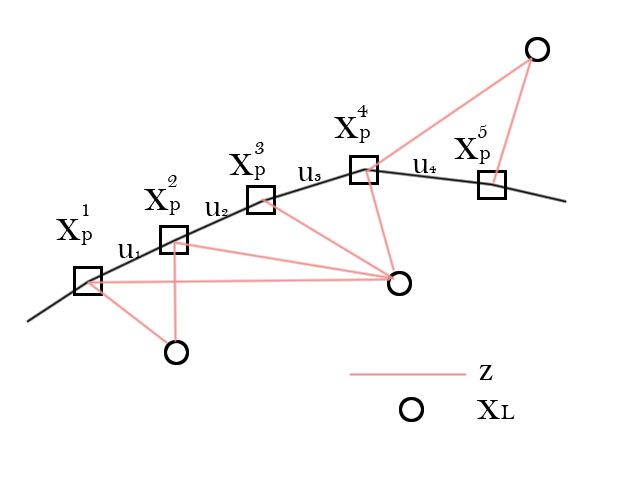
　　在求解SLAM问题前，我们要看到，我们拥有的数据是什么？在上面的模型里，我们知道的是运动信息u以及观测z。用示意图表示出来是这样的：

 

　　我们要求解的，就是根据这些u和z，确定所有的xp和xL。这就是SLAM问题的理论。从SLAM诞生开始科学家们就一直在解决这个问题。最初，我们用Kalman滤波器，所以上面的模型（运动方程和观测方程）被建成这个样子。直到21世纪初，卡尔曼滤波器仍在SLAM系统占据最主要的地位，Davison经典的单目SLAM就是用EKF做的。但是后来，出现了基于图优化的SLAM方法，渐渐有取而代之的地位[1]。我们在这里不介绍卡尔曼滤波器，有兴趣的同学可以在wiki上找卡尔曼滤波器，另有一篇中文的《卡尔曼滤波器介绍》也很棒。由于滤波器方法存储n个路标要消耗n平方的空间，在计算量上有点对不住大家。尽管08年有人提出分治法的滤波器能把复杂度弄到O(n) [2]，但实现手段比较复杂。我们要介绍那种新兴的方法: Graph-based SLAM。

　　图优化方法把SLAM问题做成了一个优化问题。学过运筹学的同学应该明白，优化问题对我们有多么重要。我们不是要求解机器人的位置和路标位置吗？我们可以先做一个猜测，猜想它们大概在什么地方。这其实是不难的。然后呢，将猜测值与运动模型／观测模型给出的值相比较，可以算出误差：

 

　　通俗一点地讲，例如，我猜机器人第一帧在(0,0,0)，第二帧在(0,0,1)。但是u1告诉我机器人往z方向（前方）走了0.9米，那么运动方程就出现了0.1m的误差。同时，第一帧中机器人发现了路标1，它在该机器人图像的正中间；第二帧却发现它在中间偏右的位置。这时我们猜测机器人只是往前走，也是存在误差的。至于这个误差是多少，可以根据观测方程算出来。

　　我们得到了一堆误差，把这些误差平方后加起来（因为单纯的误差有正有负，然而平方误差可以改成其他的范数，只是平方更常用），就得到了平方误差和。我们把这个和记作phi，就是我们优化问题的目标函数。而优化变量就是那些个xp, xL。

 

　　改变优化变量，误差平方和（目标函数）就会相应地变大或变小，我们可以用数值方法求它们的梯度和二阶梯度矩阵，然后用梯度下降法求最优值。这些东西学过优化的同学都懂的。

 

　　注意到，一次机器人SLAM过程中，往往会有成千上万帧。而每一帧我们都有几百个关键点，一乘就是几百万个优化变量。这个规模的优化问题放到小萝卜的机载小破本上可解吗？是的，过去的同学都以为，Graph-based SLAM是无法计算的。但就在21世纪06，07年后，有些同学发现了，这个问题规模没有想象的那么大。上面的J和H两个矩阵是“稀疏矩阵”，于是呢，我们可以用稀疏代数的方法来解这个问题。“稀疏”的原因，在于每一个路标，往往不可能出现在所有运动过程中，通常只出现在一小部分图像里。正是这个稀疏性，使得优化思路成为了现实。

　　优化方法利用了所有可以用到的信息（称为full-SLAM, global SLAM），其精确度要比我们一开始讲的帧间匹配高很多。当然计算量也要高一些。

　　由于优化的稀疏性，人们喜欢用“图”来表达这个问题。所谓图，就是由节点和边组成的东西。我写成G={V,E}，大家就明白了。V是优化变量节点，E表示运动/观测方程的约束。什么，更糊涂了吗？那我就上一张图，来自[3]。

 

　　图有点模糊，而且数学符号和我用的不太一样，我用它来给大家一个图优化的直观形象。上图中，p是机器人位置，l是路标，z是观测，t是位移。其中呢，p, l是优化变量，而z,t是优化的约束。看起来是不是像一些弹簧连接了一些质点呢？因为每个路标不可能出现在每一帧中，所以这个图是蛮稀疏的。不过，“图”优化只是优化问题的一个表达形式，并不影响优化的含义。实际解起来时还是要用数值法找梯度的。这种思路在计算机视觉里，也叫做Bundle Adjustment。它的具体方法请参见一篇经典文章[4]。

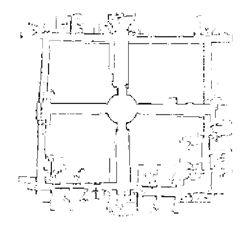
　　不过，BA的实现方法太复杂，不太建议同学们拿C来写。好在2010年的ICRA上，其他的同学们提供了一个通用的开发包：g2o [5]。它是有图优化通用求解器，很好用，我改天再详细介绍这个软件包。总之，我们只要把观测和运动信息丢到求解器里就行。这个优化器会为我们求出机器人的轨迹和路标位置。如下图，红点是路标，蓝色箭头是机器人的位置和转角（2D SLAM）。细心的同学会发现它往右偏转了一些。：

 

 

7.    闭环检测

　　上面提到，仅用帧间匹配最大的问题在于误差累积，图优化的方法可以有效地减少累计误差。然而，如果把所有测量都丢进g2o，计算量还是有点儿大的。根据我自己测试，约10000多条边，g2o跑起来就有些吃力了。这样，就有同学说，能把这个图构造地简洁一些吗？我们用不着所有的信息，只需要把有用的拿出来就行了。

　　事实上，小萝卜在探索房间时，经常会左转一下，右转一下。如果在某个时刻他回到了以前去过的地方，我们就直接与那时候采集的关键帧做比较，可以吗？我们说，可以，而且那是最好的方法。这个问题叫做闭环检测。

　　闭环检测是说，新来一张图像时，如何判断它以前是否在图像序列中出现过？有两种思路：一是根据我们估计的机器人位置，看是否与以前某个位置邻近；二是根据图像的外观，看它是否和以前关键帧相似。目前主流方法是后一种，因为很多科学家认为前一种依靠有噪声的位置来减少位置的噪声，有点循环论证的意思。后一种方法呢，本质上是个模式识别问题（非监督聚类，分类），常用的是Bag-of-Words (BOW)。但是BOW需要事先对字典进行训练，因此SLAM研究者仍在探讨有没有更合适的方法。

　　在Kinect SLAM经典大作中[6]，作者采用了比较简单的闭环方法：在前面n个关键帧中随机采k个，与当前帧两两匹配。匹配上后认为出现闭环。这个真是相当的简单实用，效率也过得去。

　　高效的闭环检测是SLAM精确求解的基础。这方面还有很多工作可以做。

8.    小结

　　本文我们介绍了SLAM的基本概念，重点介绍了图优化解决SLAM问题的思路。我最近正在编写SLAM程序，它是一个Linux下基于cmake的工程。目前仍在开发当中。欢迎感兴趣的同学来交流研究心得，我的邮件是：[email protected]。

参考文献

[1] Visual SLAM: Why filter? Strasdat et. al., Image and Vision Computing, 2012.

[2] Divide and Conquer: EKF SLAM in O(n), Paz Lina M et al., IEEE Transaction on Robotics, 2008

[3] Relative bundle adjustment, Sibley, Gabe, 2009

[4] Bundle adjustment - a Modern Synthesis. Triggs B et. el., Springer, 2000

[5] g2o: A General Framework for Graph Optimization, Kummerle Rainer, et. al., ICRA, 2011

[6] 3-D Mapping with an RGB-D Camera, IEEE Transaction on Robotics, Endres et al., 2014

视觉SLAM漫谈 (三): 研究点介绍

1.　　前言

　　读者朋友们大家好！（很久很久）之前，我们为大家介绍了SLAM的基本概念和方法。相信大家对SLAM，应该有了基本的认识。在忙完一堆写论文、博士开题的事情之后，我准备回来继续填坑：为大家介绍SLAM研究的方方面面。如果前两篇文章算是"初识"，接下来几篇就是"渐入佳境"了。在第三篇中，我们要谈谈SLAM中的各个研究点，为研究生们（应该是博客的多数读者吧）作一个提纲挈领的摘要。然后，我们再就各个小问题，讲讲经典的算法与分类。我有耐心讲，你是否有耐心听呢？

　　在《SLAM for Dummy》中，有一句话说的好："SLAM并不是一种算法，而是一个概念。（SLAM is more like a concept than a single algorithm.）"所以，你可以和导师、师兄弟（以及师妹，如果有的话）说你在研究SLAM，但是，作为同行，我可能更关心：你在研究SLAM中的哪一个问题。有些研究者专注于实现一个具体的SLAM系统，而更多的人则是在研究SLAM里某些方法的改进。做应用和做理论的人往往彼此看不起，不过二者对科研都是有贡献的。作为研究生，我还是建议各位抓住SLAM中一个小问题，看看能否对现有的算法进行改进或者比较。不要觉得这种事情肤浅，它是对研究有实际帮助和意义的。同时，我也有一些朋友，做了一个基于滤波器/图优化的SLAM实现。程序是跑起来了，但他/她不知道自己有哪些贡献，钻研了哪个问题，写论文的时候就很头疼。所以，作为研究生，我建议你选择SLAM中的一个问题，改进其中的算法，而不是先找一堆程序跑起来再说。

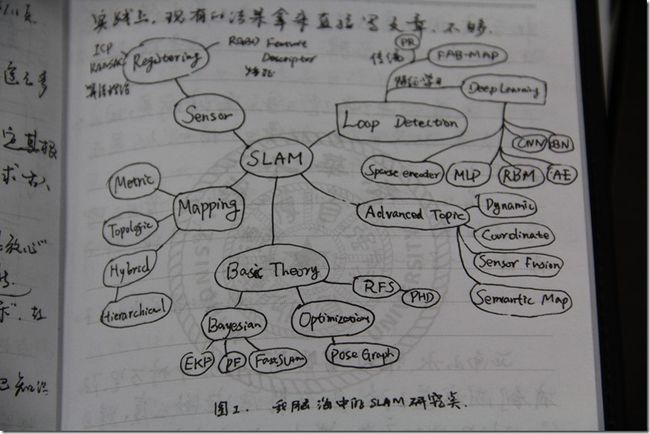
　　那么问题来了：SLAM方面究竟有哪些可以研究的地方呢？我为大家上一个脑图。

　　这个图是从我笔记本上拍下来的（请勿吐槽字和对焦）。可以看到，以SLAM为中心，有五个圈连接到它。我称它为Basic Theory（基础理论）、Sensor（传感器）、Mapping（建图）、Loop Detection（回环检测）、Advanced Topic（高级问题）。这可以说是SLAM的研究方向。下面我们"花开五朵，各表一枝"。

2.　　基本理论

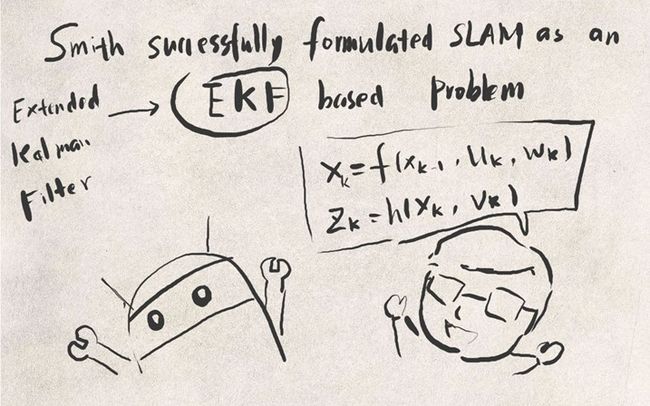
　　SLAM的基本理论，是指它的数学建模。也就是你如何用数学模型来表达这个问题。为什么说它"基本"呢？因为数学模型影响着整个系统的性能，决定了其他问题的处理方法。在早先的研究中（86年提出[1]至21世纪前期[2]），是使用卡尔曼滤波器的数学模型的。那里的机器人，就是一个位姿的时间序列；而地图，就是一堆路标点的集合。什么是路标点的集合？就是用 (x,y,z) 表示每一个路标，然后在滤波器更新的过程中，让这三个数慢慢收敛。

　　那么，请问这样的模型好不好？

　　好处是可以直接套用滤波器的求解方法。卡尔曼滤波器是很成熟的理论，比较靠谱。

　　缺点呢？首先，滤波器有什么缺点，基于它的SLAM就有什么缺点。所以EKF的线性化假设啊，必须存储协方差矩阵带来的资源消耗啊，都成了缺点（之后的文章里会介绍）。然后呢，最直观的就是，用 (x,y,z) 表示路标？万一路标变了怎么办？平时我们不就把屋里的桌子椅子挪来挪去的吗？那时候滤波器就挂了。所以啊，它也不适用于动态的场合。

　　这种局限性就是数学模型本身带来的，和其他的算法无关。如果你希望在动态环境中跑SLAM，就要使用其他模型或改进现有的模型了。

　　SLAM的基本理论，向来分为滤波器和优化方法两类。滤波器有扩展卡尔曼滤波（EKF）、粒子滤波（PF），FastSLAM等，较早出现。而优化方向用姿态图（Pose Graph），其思想在先前的文章中介绍过。近年来用优化的逐渐增多，而滤波器方面则在13年出现了基于Random Finite Set的方法[3]，也是一个新兴的浪潮[4]。关于这些方法的详细内容，我们在今后的文章中再进行讨论。

　　作为SLAM的研究人员，应该对各种基本理论以及优缺点有一个大致的了解，尽管它们的实现可能非常复杂。

3.　　传感器

　　传感器是机器人感知世界的方式。传感器的选择和安装方式，决定了观测方程的具体形式，也在很大程度上影响着SLAM问题的难度。早期的SLAM多使用激光传感器（Laser Range Finder），而现在则多使用视觉相机、深度相机、声呐（水下）以及传感器融合。我觉得该方向可供研究点有如下几个：

• 如何使用新兴传感器进行SLAM。    要知道传感器在不断发展，总有新式的东西会出来，所以这方面研究肯定不会断。
• 不同的安装方式对SLAM的影响。    举例来说，比如相机，顶视（看天花板）和下视（看地板）的SLAM问题要比平视容易很多。为什么容易呢？因为顶/下视的数据非常稳定，不像平视，要受各种东西的干扰。当然，你也可以研究其他的安装方式。
• 改进传统传感器的数据处理。        这部分就有些困难了，因为经常传感器已经有很多人在使用，你做的改进，未必比现有的成熟方法更好。

4.　　建图

　　建图，顾名思议，就是如何画地图呗。其实，如果知道了机器人的真实轨迹，画地图是很简单的一件事。不过，地图的具体形式也是研究点之一。比如说常见的有以下几种：

• 路标地图。       

　　地图由一堆路标点组成。EKF中的地图就是这样的。但是，也有人说，这真的是地图吗（这些零零碎碎的点都是什么啊喂）？所以路标图尽管很方便，但多数人对这种地图是不满意的，至少看上去不像个地图啊。于是就有了密集型地图（Dense map）。

• 度量地图（Metric map）    

　　通常指2D/3D的网格地图，也就是大家经常见的那种黑白的/点云式地图。点云地图比较酷炫，很有种高科技的感觉。它的优点是精度比较高，比如2D地图可以用0-1表示某个点是否可通过，对导航很有用。缺点是相当吃存储空间，特别是3D，把所有空间点都存起来了，然而大多数角角落落里的点除了好看之外都没什么意义……

• 拓扑地图（Topological map）       

　　拓扑地图是比度量地图更紧凑的一种地图。它将地图抽象为图论中的"点"和"边"，使之更符合人类的思维。比如说我要去五道口，不知道路，去问别人。那人肯定不会说，你先往前走621米，向左拐94.2度，再走1035米……（这是疯子吧）。正常人肯定会说，往前走到第二个十字路口，左拐，走到下一个红绿灯，等等。这就是拓扑地图。

• 混合地图。        

　　既然有人要分类，就肯定有人想把各类的好处揉到一起。这个就不多说了吧。

5.　　回环检测

　　回环检测，又称闭环检测（Loop closure detection），是指机器人识别曾到达场景的能力。如果检测成功，可以显著地减小累积误差。

　　回环检测目前多采用词袋模型（Bag-of-Word），研究计算机视觉的同学肯定不会陌生。它实质上是一个检测观测数据相似性的问题。在词袋模型中，我们提取每张图像中的特征，把它们的特征向量（descriptor）进行聚类，建立类别数据库。比如说，眼睛、鼻子、耳朵、嘴等等（实际当中没那么高级，基本上是一些边缘和角）。假设有10000个类吧。然后，对于每一个图像，可以分析它含有数据库中哪几个类。以1表示有，以0表示没有。那么，这个图像就可用10000维的一个向量来表达。而不同的图像，只要比较它们的向量即可。

　　回环检测也可以建成一个模型识别问题，所以你也可以使用各种机器学习的方法来做，比如什么决策树/SVM，也可以试试Deep Learning。不过实际当中要求实时检测，没有那么多时间让你训练分类器。所以SLAM更侧重在线的学习方法。

6.　　高级话题

　　前面的都是基础的SLAM，只有"定位"和"建图"两件事。这两件事在今天已经做的比较完善了。近几年的RGB-D SLAM[5], SVO[6], Kinect Fusion[7]等等，都已经做出了十分炫的效果。但是SLAM还未走进人们的实际生活。为什么呢？

　　因为实际环境往往非常复杂。灯光会变，太阳东升西落，不断的有人从门里面进进出出，并不是一间安安静静的空屋子，让一个机器人以2cm/s的速度慢慢逛。论文中看起来酷炫的算法，在实际环境中往往捉襟见肘，处处碰壁。向实际环境挑战，是SLAM技术的主要发展方向，也就是我们所说的高级话题。主要有：动态场景、语义地图、多机器人协作等等。

7.　　小结

　　本文向大家介绍了SLAM中的各个研究点。我并不想把它写成综述，因为不一定有人愿意看一堆的参考文献，我更想把它写成小故事的形式。

　　最后，让我们想象一下未来SLAM的样子吧：

　　有一天，小萝卜被领进了一家新的实验楼。在短暂的自我介绍之后，他飞快地在楼里逛了一圈，记住了哪里是走廊，哪儿是房间。他刻意地观察各个房间特有的物品，以便区分这些看起来很相似的房间。然后，他回到了科学家身边，协助他的研究。有时，科学家会让他去各个屋里找人，找资料，有时，也带着他去认识新安装的仪器和设备。在闲着没事时，小萝卜也会在楼里逛逛，看看那些屋里都有什么变化。每当新的参观人员到来，小萝卜会给他们看楼里的平面图，向他们介绍各个楼层的方位与状况，为他们导航。大家都很喜欢小萝卜。而小萝卜明白，这一切，都是过去几十年里SLAM研究人员不断探索的结果。

 

References:

[1].    Smith, R.C. and P. Cheeseman, On the Representation and Estimation of Spatial Uncertainty. International Journal of Robotics Research, 1986. 5(4): p. 56--68.

[2].    Se, S., D. Lowe and J. Little, Mobile robot localization and mapping with uncertainty using scale-invariant visual landmarks. The international Journal of robotics Research, 2002. 21(8): p. 735--758.

[3].    Mullane, J., et al., A Random-Finite-Set Approach to Bayesian SLAM. IEEE Transactions on Robotics, 2011.

[4].    Adams, M., et al., SLAM Gets a PHD: New Concepts in Map Estimation. IEEE Robotics Automation Magazine, 2014. 21(2): p. 26--37.

[5].    Endres, F., et al., 3-D Mapping With an RGB-D Camera. IEEE Transactions on Robotics, 2014. 30(1): p. 177--187.

[6].    Forster, C., M. Pizzoli and D. Scaramuzza, SVO: Fast semi-direct monocular visual odometry. 2014, IEEE. p. 15--22.

[7].    Newcombe, R.A., et al., KinectFusion: Real-time dense surface mapping and tracking. 2011, IEEE. p. 127--136.