【HDU5515 2015沈阳赛区G】【解方程or二分 模拟】Game of Flying Circus 跑垒游戏 【翻译错误 出题事故】

Game of Flying Circus Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 101    Accepted Submission(s): 27 Problem Description The discovery of anti-gravitations technology changed the world. The invention of anti-gravitation shoes (Grav-shoes) enables people to fly in the sky freely. This led to the rise of a new sky sport:   ``Flying Circus". Utilizing Grav-shoes and personal flying suits, competitors battle it out in a special field, where they compete scoring obtain   m  points within a certain time limit. The field is a square with edge length   300  meters. Moreover, there are four buoys floating at each corner of the square. Four buoys are numbered as   1,2,3,4  in clockwise order. Two players start at buoy   #1 . When game begin, they will try to touch four floating buoys in clockwise order. (Since buoy   #1  is the start point, the first buoy they need to touch will be buoy   #2 , and after that, they need to touch buoy   #3,#4,#1  in order)   Note that they could fly freely in the field, even fly inside the square field. Under two situations the player could score one point. ⋅ 1.  If you touch a buoy before your opponent, you will get one point.  For example if your opponent touch the buoy   #2  before you after start, he will score one point. So when you touch the buoy   #2 , you won't get any point. Meanwhile, you cannot touch buoy   #3  or any other buoys before touching the buoy   #2 . ⋅ 2.  Ignoring the buoys and relying on dogfighting to get point.  If you and your opponent meet in the same position, you can try to fight with your opponent to score one point. For the proposal of game balance, two players are not allowed to fight before buoy   #2  is touched by anybody. There are three types of players. Speeder: As a player specializing in high speed movement, he/she tries to avoid dogfighting while attempting to gain points by touching buoys. Fighter: As a player specializing in dogfighting, he/she always tries to fight with the opponent to score points. Since a fighter is slower than a speeder, it's difficult for him/her to score points by touching buoys when the opponent is a speeder. All-Rounder: A balanced player between Fighter and Speeder. There will be a training match between Asuka (All-Rounder) and Shion (Speeder). Since the match is only a training match, the rules are simplified:   the game will end after the buoy   #1   is touched by anybody. Shion is a speed lover, and his strategy is very simple: touch buoy   #2,#3,#4,#1  along the shortest path. Asuka is good at dogfighting, so she will always score one point by dogfighting with Shion, and   the opponent will be stunned for T seconds after dogfighting.Since Asuka is slower than Shion, she decides to fight with Shion for only one time during the match. It is also assumed that if Asuka and Shion touch the buoy in the same time, the point will be given to Asuka and Asuka could also fight with Shion at the buoy. We assume that in such scenario, the dogfighting must happen after the buoy is touched by Asuka or Shion. The speed of Asuka is   V1 m/s . The speed of Shion is   V2 m/s . Is there any possibility for Asuka to win the match (to have higher score)?   Input The first line contains an integer   t (0<t≤1000) , followed by   t  lines. Each line contains three double   T, V1  and   V2 (0≤V1≤V2≤2000,0≤T≤2000)  with no more than two decimal places, stands for one case.   Output If there exist any strategy for Asuka to win the match, output ``Yes", otherwise, output ``No".   Sample Input 2 1 10 13 100 10 13   Sample Output Case #1: No Case #2: Yes Hint Asuka could fly to the mid point of the edge between buoy #2 and buoy #3, and wait there until Shion come. Asuka will fight with Shion when they meet. As a result, Shion will be stunned (It means Shion cannot move for 100 seconds.) Then Asuka could fly back to buoy #2, since the buoy #2 is touched, she will get no point by touching buoy #2. But after that, she could fly to buoy #3, #4, #1 along the edge and get three points.   Source 2015ACM/ICPC亚洲区沈阳站-重现赛（感谢东北大学）

 

翻译错+翻译漏的英文翻译(对应原文倒数第二段)：

 It is also assumed that if Asuka and Shion touch the buoy in the same time, the point will be given to Asuka and Asuka could also fight with Shion at the buoy. We assume that in such scenario, the dogfighting must happen after the buoy is touched by Asuka or Shion.

#include<stdio.h>
#include<string.h>
#include<ctype.h>
#include<math.h>
#include<iostream>
#include<string>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre(){freopen("c://test//input.in","r",stdin);freopen("c://test//output.out","w",stdout);}
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T> inline void gmax(T &a,T b){if(b>a)a=b;}
template <class T> inline void gmin(T &a,T b){if(b<a)a=b;}
const int N=0,M=0,Z=1e9+7,ms63=1061109567;
int casenum,casei;
double T,v1,v2,T1,T2;
double K(double x){return x*x;}
void YES(){printf("Case #%d: Yes\n",casei);}
void NO(){printf("Case #%d: No\n",casei);}
void solve()
{	
	if(v1==v2)YES();
	else if(v1*v1*2>v2*v2)//最早能在#3之前相遇，二分相遇点的横坐标
	{
		double l=0;
		double r=300;
		for(int tim=1;tim<=100;tim++)
		{
			double m=(l+r)/2;
			double l1=sqrt(K(300)+K(m));
			double t1=l1/v1;
			double l2=300+m;
			double t2=l2/v2;
			t1>t2?l=m:r=m;//如果来不及，那么相遇点横坐标变大，否则横坐标变小。
		}
		//如果我们想要获胜，必须至少要触碰#3和#4。
		double t1=sqrt(K(300)+K(l))/v1+l/v1+2*T1;//我们触碰#4的时间
		double t2=3*T2+T;//对手触碰#4的时间
		t1<=t2?YES():NO();
	}
	else if(v1*3>v2)//最早能在#4之前相遇，二分相遇点的纵坐标
	{
		double l=0;
		double r=300;
		for(int tim=1;tim<=100;tim++)
		{
			double m=(l+r)/2;
			double l1=sqrt(K(300)+K(m));
			double t1=l1/v1;
			double l2=900-m;
			double t2=l2/v2;
			t1>t2?r=m:l=m;//如果来不及，那么相遇点纵坐标变小，否则纵坐标变大。
		}
		//如果我们想要获胜，必须至少要触碰#4和#1
		double xx=sqrt(K(300)+K(l))/v1;
		double yy=sqrt(K(300)+K(300-l))/v1;
		double t1=sqrt(K(300)+K(l))/v1+sqrt(K(300)+K(300-l))/v1+3*T1;//我们触碰#1的时间
		double t2=4*T2+T;//对手触碰#1的时间
		t1<=t2?YES():NO();
	}
	else NO();
}
int main()
{
	scanf("%d",&casenum);
	for(casei=1;casei<=casenum;casei++)
	{
		scanf("%lf%lf%lf",&T,&v1,&v2);
		T1=300/v1;
		T2=300/v2;
		solve();
	}
	return 0;
}
/*
【trick&&吐槽】
1，这题让我懂得了：对于很多坑题，要一句句全部读懂才能做。
有的作者重点极其分散，使得题目像是阅读理解一样来考你。而且最后还要自行脑补题意。

2，有的题目，对于重要信息，题目上下文会多次重复提及。
然而也有题目，上下文看似相同的两处信息，其实要有不一样的理解。

3，噢。在我整理这道题题解的时候，从出题人处得到了中文题。发现这题认真理解题意的话，就是个翻译错的题。
需要脑补才能AC，脑补才能AC，脑补才能AC……你要多读，多猜，多想，自行发现哪里可能有歧义。
翻译是把reach和touch搞错了。而且原文消除歧义的一大段文字，在翻译中一字未现。
所以才导致了各种无限wa的情况，甚至包括做CodeChef擅长阅读理解的朝鲜人12wa未AC。

【题意】
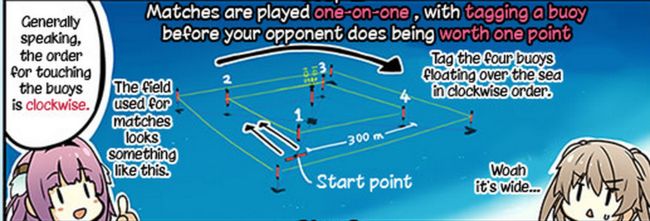
一个正方形球场。每个角都有一个浮标。按照顺时针方向，依次编号为#1，#2，#3，#4。
两个运动员开始都在1号球杆，他们要先后触碰2号，3号，4号，1号球杆，绕圈一周。

游戏规则：
1，对于任何一个浮标，如果你触碰的时间比对手早，那么你可以得到1分。但是触碰浮标的顺序必须严格是#2，#3，#4，#1。
2，如果你和对手同时到达了一个位置。你们可以打一场，赢的人得一分。但是为了保证比赛的平衡，2个运动员不允许在#2被触碰之前打架。

我们的速度是v1，对手的速度是v2，满足：0<v1<=v2<=2000。
对手会严格按照矩形的边，即按照1->2->3->4->1的顺序移动。
我们一定能打过对手，于是我们决定触发有且仅有一次战斗。这会使得我们多得到1分，并且使得对手立刻眩晕T秒。
如果2个人同时到触碰一个点，这个点的得分会给与我们，且我们还可以发动与对手的战斗。
如果2个人恰好在一个点相遇，如果对手碰过上一个浮标，那这个点的得分会给对手。
让你输出是否我们有可能得分比对手高。可能便输出Yes，不可能则输出No。

【类型】
阅读理解 解方程 坑B题

【分析】
这题的逻辑可以很清楚。
1，如果速度相同，那么我们必胜。
2，如果速度不同，我们有意义的阻截位置，要不是在2->3，要不是在3->4。
因为我们最终肯定要沿着#2->#3->#4->#1的顺序走，所以肯定满足——触碰位置越早越好。

所以存在三个判定点，
1，速度相同，我方必胜。
2，[#2 ~ #3)之间相遇，看我方能否先到达#4。
3，[#3 ~ #4)之间相遇，看我方能否先到达#1。
4，[#4 ~ #1)相遇，我方必败。

【时间复杂度&&优化】
O（T*二分）

【数据】
Input
2
1 10 13
100 10 13

Output
Case #1: No
Case #2: Yes

specail(恰好相遇于#4):
2000 100 300
我们和对方都同时在第3s到达，我方必败。

special(恰好相遇于#4前):
2000 100.01 300
眩晕时间很长，我方胜。

special[1+]
12.25 100.01 300
恰好胜

special[2+]
12.24 100.01 300
恰好败
*/