Delta-wave
Problem Link: http://acm.hdu.edu.cn/showproblem.php?pid=1030
Delta-wave
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 5641 Accepted Submission(s): 2147
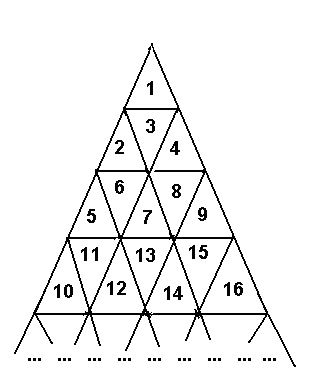
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
6 12
3
在看这题之前,我们先看下一个简单的题目
图示两个点,如果只能横向或者纵线走,从A到B的步数为(5-2)+(3-1)=5
在此坐标系中,每个方格有两个方向(横向、纵向,即x,y方向)
那么在此题中,不难看出每个三角形有三个方向(x,y,z)
Z方向
有了这些基础之后,我们需要求解的就是在某点在各个方向上面的位置
例如:点n在三个方向的坐标为:
X=(int)sqrt(n-1)+1;
Y= (n - (X-1)*(X-1)+1)/2;
Z= (X*X - n)/2+1;
下面就是我个人对以上得出的公式的推导过程:
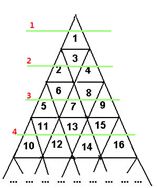
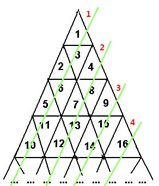
首先,X表示点n所在位置从上到下为第X层,Y表示点n所在位置从左上到右下第Y层,Z表示点n所在位置从右上到左下第Z层。
观察每一行的点,不难发现规律:
1.每一行最后一个数都是该行的平方值。
2.对于求某一点左上到右下是第几层,等于该点的值减去所在的上一行最后一个数之后除以2,再加上1(为什么要除以2和加1呢?下面再细说)。
3.对于求某一点右上到左下是第几层,等于该点所在行最后一个数减去该点的值之后加上1,再除以2(为什么要除以2和加1呢?下面再细说)。
解释:
除了第一行外,对其他任意一行上的一点,无论该点左上到右下或从右上到左下,总有一个与它同在一个水平方向上(即同行)并与它相邻的点属于同一层次,即左上到右下或从右上到左下这两个方向上有两个水平方向相邻的数是在同一层上,因此求一点在这两个方向是第几层都要除以2。加1主要是由该点的位置及以上条件所决定的,这样确保所求位置方向坐标准确。读者可参考上图加以理解,我就不赘诉了。。。
c代码如下:
#include<stdio.h>
#include<math.h>
int calculate_x(int n)//从上到下数第x层
{
return (int)sqrt(n-1)+1;// x=(int)sqrt(n-1)+1
}
int calculate_y(int n,int x)//从左上到右下第y层
{
return (n-(x-1)*(x-1)+1)/2;//第x层最左端的数为(x-1)^2+1 , 最右端的数为x^2
}
int calculate_z(int n,int x)//从右上到左下第z层
{
return (x*x-n)/2+1;
}
int main()
{
int n,m,x1,x2,y1,y2,z1,z2,s;
while(scanf("%d%d",&n,&m)!=EOF)//分别计算出n,m的x,y,z
{
x1=calculate_x(n);
y1=calculate_y(n,x1);
z1=calculate_z(n,x1);
x2=calculate_x(m);
y2=calculate_y(m,x2);
z2=calculate_z(m,x2);
s=abs(x1-x2)+abs(y1-y2)+abs(z1-z2);
printf("%d\n",s);
}
return 0;
}
然后AC...功成身已退![]()
莫笑在下,纯属自娱自乐,欢迎各位大牛指点哈,不甚感激。。。