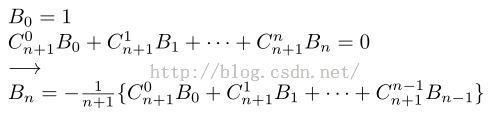自然数幂之和

简单的说，问题就是：

不同的问题随着k的大小变化解法也要求相应的进化。

zoj A very easy task

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1864

相关数据： (0 <= n <= 10⁵⁰, 1 <= k <= 100)

二项式展开：
进一步得到：
把n变成n-1,n-2,''',1：




上式累加：

换元：

k不断减小，直到递归到k=1，那么S(n,1)=(n+1)n/2; 时间复杂度：O(n^2)
import java.util.*;
import java.math.BigInteger;
public class Main {
	static final int N=110;
    static BigInteger []ans=new BigInteger [N];
    static BigInteger [][] C=new BigInteger[N][N];
    static void init(){
    	for(int i=1;i<N;i++){
    		C[i][0]=C[i][i]=BigInteger.ONE;
    		for(int j=1;j<i;j++){
    			C[i][j]=C[i-1][j-1].add(C[i-1][j]);
    		}
    	}
    }
    static BigInteger solve(BigInteger n,int k){
    	if(ans[k].compareTo(BigInteger.valueOf(-1))!=0){
    		return ans[k];
    	}
    	if(k==1){
    		ans[k]=(n.add(BigInteger.ONE)).multiply(n).divide(BigInteger.valueOf(2));
    	    return ans[k];
    	}
    	BigInteger t=BigInteger.ONE,temp=BigInteger.ZERO;
    	for(int i=0;i<k+1;i++){
    		t=t.multiply(n.add(BigInteger.ONE));
    	}
    	t=t.subtract(n.add(BigInteger.ONE));
    	for(int i=1;i<k;i++){
    		temp=temp.add(C[k+1][k+1-i].multiply(solve(n,i)));
    	}
    	t=t.subtract(temp);
    	ans[k]=t.divide(BigInteger.valueOf(k+1));
    	return ans[k];
    }
	public static void main(String[] args) {
		init();
		BigInteger n;
		int k;
		Scanner cin=new Scanner (System.in);
		while(cin.hasNext()){
			n=cin.nextBigInteger();
			k=cin.nextInt();
			for(int i=0;i<N;i++){
				ans[i]=BigInteger.valueOf(-1);
			}
			System.out.println(solve(n,k));
		}

	}

}

51nod 1228 序列求和

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1228

相关数据：(1 <= N <= 10^18, 1 <= K <= 2000)

T(n) = n^k，S(n) = T(1) + T(2) + ...... T(n)。给出n和k，求S(n)。
  
  
  
  

   
   
   
   例如k = 2，n = 5，S(n) = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55。
  
  
  
  
  
  
  
  

   
   
   
   由于结果很大，输出S(n) Mod 1000000007的结果即可。
  
  
  
  
  
  
  
  

   
   
   
   分析：有5000case，自然数幂之和的普通解法O(k^2)，故另辟蹊径。借助ACdreamer大神的思路，该问题和伯努利数联系。有这样的等式： 
  
  
  
  
  
  
  
  

   
   
   
   顺便回忆了一下逆元的相关知识，万能的求解，这里需要K=1-->2000，k+1 mod 1000000007的逆，可以使用递推逆元的方法预处理：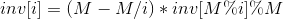 
  
  
  
  
  
  
  
  

   
   
   
   相关证明：http://blog.csdn.net/acdreamers/article/details/8220787
  
  
  
  
  
  
  
  

   
   
   
   
   
   
   
   
 
    组合数C(n,m)同样预处理。 
   
   
   
   
   
 
    最后的伯努利： 
   
   
   
   
    
  
  
  
  
  
  
  
  

   
   
   
   mod操作，小心又小心，不要少加%mod。 
  
  
  
  
  
  
  
  

   
   
   
   
   
   
   
   
import java.util.*;
public class Main {
 static final int N=2005,mod=1000000007;
    static long [][]C=new long [N][N];
 static long []inv=new long [N],B=new long [N],nadd1=new long [N];
    static void initC(){
  C[0][0]=1;
  for(int i=1;i<N;i++){
   C[i][0]=C[i][i]=1;
   for(int j=1;j<i;j++)
       C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
  }
 }
 static void initinv(){
  inv[1]=1;
  for(int i=2;i<N;i++){
   inv[i]=(mod-mod/i)*inv[mod%i]%mod;
  }
 }
 static void initB(){
  B[0]=1;
  for(int i=1;i<N;i++){
   if(i==N-1) break;
   for(int j=0;j<i;j++){
    B[i]=(B[i]+C[i+1][j]*B[j]%mod)%mod;
   }
   B[i]=B[i]*(-inv[i+1]);
   B[i]=(B[i]%mod+mod)%mod;
  }
 }
    public static void main(String[] args) {
  int t,k;
  long n;
  Scanner cin=new Scanner (System.in);
  t=cin.nextInt();
  initC();  
  initinv();
  initB();  
  while(t>0){
   t--;
   n=cin.nextLong();
   n=n%mod; //!!
   k=cin.nextInt();
   nadd1[0]=1;
   for(int i=1;i<=k+1;i++){
    nadd1[i]=nadd1[i-1]*(n+1)%mod;
   }
   long ans=0;
   for(int i=1;i<=k+1;i++){
    ans=(ans+C[k+1][i]*B[k+1-i]%mod*nadd1[i]%mod)%mod;
   }
   ans=(ans*inv[k+1]%mod+mod)%mod;
   System.out.println(ans);
  }
 }

}

   
   
   
   当k达到万级时，又是一个工程，我还得继续学习。。。||-_-