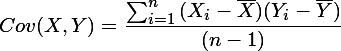主成分分析PCA

华夏35度

Data Mining

主成分分析PCA

降维的必要性

1.多重共线性--预测变量之间相互关联。多重共线性会导致解空间的不稳定，从而可能导致结果的不连贯。

2.高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有0.02%。

3.过多的变量会妨碍查找规律的建立。

4.仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。

降维的目的：

1.减少预测变量的个数

2.确保这些变量是相互独立的

3.提供一个框架来解释结果

降维的方法有：主成分分析、因子分析、用户自定义复合等。

 

PCA（Principal Component Analysis）不仅仅是对高维数据进行降维，更重要的是经过降维去除了噪声，发现了数据中的模式。

PCA把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合，这些线性组合最大化样本方差，尽量使新的m个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。

预备知识

样本X和样本Y的协方差(Covariance)：

协方差为正时说明X和Y是正相关关系，协方差为负时X和Y是负相关关系，协方差为0时X和Y相互独立。

Cov(X,X)就是X的方差(Variance).

当样本是n维数据时，它们的协方差实际上是协方差矩阵（对称方阵），方阵的边长是。比如对于3维数据(x,y,z)，计算它的协方差就是：

若，则称是A的特征值，X是对应的特征向量。实际上可以这样理解：矩阵A作用在它的特征向量X上，仅仅使得X的长度发生了变化，缩放比例就是相应的特征值。

当A是n阶可逆矩阵时，A与P^-1Ap相似，相似矩阵具有相同的特征值。

特别地，当A是对称矩阵时，A的奇异值等于A的特征值，存在正交矩阵Q（Q^-1=Q^T），使得：

对A进行奇异值分解就能求出所有特征值和Q矩阵。

     D是由特征值组成的对角矩阵

由特征值和特征向量的定义知，Q的列向量就是A的特征向量。

Jama包

Jama包是用于基本线性代数运算的java包，提供矩阵的cholesky分解、LUD分解、QR分解、奇异值分解，以及PCA中要用到的特征值分解，此外可以计算矩阵的乘除法、矩阵的范数和条件数、解线性方程组等。

PCA过程

1.特征中心化。即每一维的数据都减去该维的均值。这里的“维”指的就是一个特征（或属性），变换之后每一维的均值都变成了0。

很多数据挖掘的教材上都会讲到鹫尾花的例子，本文就拿它来做计算。原始数据是150×4的矩阵A：

+ View Code

每一列减去该列均值后，得到矩阵B：

+ View Code

2.计算B的协方差矩阵C:

+ View Code

3.计算协方差矩阵C的特征值和特征向量。

C=V*S*V ^-1

S=

4.2248414 　　　　0 　　　　　　0 　　　　　　0 
0 　　　　　　　　 0.24224437 　0 　　　　 　   0 
0 　　　　　　　　 0 　　　　　　0.078524387   0 
0 　　　　　　　　 0 　　　　　　0 　　　　　　 0.023681839

V=

0.36158919 　　0.65654382 　　-0.58100304 　　0.3172364 
-0.082268924 　　 0.72970845 　　 0.596429220 　　    -0.3240827 
0.85657212　　-0.17576972 0.　　072535217 　　 -0.47971643 
0.35884438 　　 -0.074704743 　　 0.54904125 　　 0.75113489

4.选取大的特征值对应的特征向量，得到新的数据集。

特征值是由大到小排列的，前两个特征值的和已经超过了所有特征值之和的97%。我们取前两个特征值对应的特征向量，得到一个4×2的矩阵M。令A' _150×2=A _150×4M _4×2，这样我们就把150×4的数据A集映射成了150×2的数据集A'，特征由4个减到了2个。

A'=

+ View Code

每个样本正好是二维的，画在平面坐标系中如图：

鹫尾花数据集共分为3类花（前50个样本为一类，中间50个样本为一类，后50个样本为一类），从上图可以看到把数据集映射到2维后分类会更容易进行，直观上看已经是线性可分的了，下面我们用自组织映射网络对其进行聚类。

当然我们已知了有3类，所以在设计SOFM网络时，我把竞争层节点数设为3，此时的聚类结果是前50个样本聚为一类，后100个样本聚为一类。当把竞争层节点数改为4时，仅第2类中的3个样本被误分到了第3类中，整体精度达98%！

#include<iostream>
#include<fstream>
#include<set>
#include<cstdlib>
#include<vector>
#include<cmath>
#include<ctime>

using  namespace  std;

const  int  sample_num=150;      //鹫尾花样本个数
const  int  class_num=4;      //指定聚类的数目
int  iteration_ceil;      //迭代的上限
vector<pair< double , double > > flowers(sample_num);      //样本数据
vector<vector< double > > weight(class_num);   //权向量
const  double  prime_eta=0.7;     //初始学习率

/*向量模长归一化*/
void  normalize(vector< double > &vec){
    double  sum=0.0;
    for ( int  i=0;i<vec.size();++i)
        sum+= pow (vec[i],2);
    sum= sqrt (sum);
    for ( int  i=0;i<vec.size();++i)
        vec[i]/=sum;
}

/*从文件读入鹫尾花样本数据*/
void  init_sample(string filename){
    ifstream ifs(filename.c_str());
    if (!ifs){
        cerr<< "open data file failed." <<endl;
        exit (1);
    }
    for ( int  i=0;i<sample_num;++i){
        vector< double > X(2);
        ifs>>X[0]>>X[1];
        normalize(X);       //输入向量模长归一化
        flowers[i]=make_pair(X[0],X[1]);
    }
    ifs.close();
}

/*初始化权值*/
void  init_weight(){
    srand ( time (0));
    for ( int  i=0;i<weight.size();++i){
        vector< double > ele(2);
        ele[0]= rand ()/( double )RAND_MAX;
        ele[1]= rand ()/( double )RAND_MAX;
        normalize(ele);     //权值向量模长归一化
        weight[i]=ele;
    }
}

/*根据输入，选择获胜者*/
int  pick_winner( double  x1, double  x2){
    int  rect=-1;
    double  max=0.0;
    for ( int  i=0;i<weight.size();++i){
        double  product=x1*weight[i][0]+x2*weight[i][1];
        if (product>max){
            max=product;
            rect=i;
        }
    }
    return  rect;
}

int  main( int  argc, char  *argv[]){
    cout<< "input iteration count" <<endl;
    int  count;      //每个样本迭代的次数
    cin>>count;
    cout<< "input data file name" <<endl;
    string filename;
    cin>>filename;
    iteration_ceil=count*sample_num;
    init_sample(filename);
    init_weight();

    double  eta=prime_eta;
    double  gradient1=-1*9*prime_eta/iteration_ceil;
    double  gradient2=-1*prime_eta/(9*iteration_ceil);
    double  b1=prime_eta;
    double  b2=prime_eta/9;
    for ( int  iteration=0;iteration<iteration_ceil;++iteration){
        int  flower_index=iteration%sample_num;
        double  x1=flowers[flower_index].first;
        double  x2=flowers[flower_index].second;
        int  winner=pick_winner(x1,x2);
        /*更改获胜者的权值*/
        weight[winner][0]+=eta*(x1-weight[winner][0]);
        weight[winner][1]+=eta*(x2-weight[winner][1]);
        /*权向量归一化*/
        for ( int  i=0;i<weight.size();++i){
            vector< double > W(2);
            W[0]=weight[i][0];
            W[1]=weight[i][1];
            normalize(W);
            weight[i][0]=W[0];
            weight[i][1]=W[1];
        }
        /*更新学习率*/
        if (iteration<0.1*iteration_ceil){   //在前10%的迭代中，学习率线性下降到原来的10%
            eta=gradient1*iteration+b1;
        }
        else {       //后90%的迭代中线性降低到0
            eta=gradient2*iteration+b2;
        }
    }

    for ( int  i=0;i<sample_num;++i){
        double  x1=flowers[i].first;
        double  x2=flowers[i].second;
        int  winner=pick_winner(x1,x2);
        cout<<i+1<< "\t" <<winner+1<<endl;
    }
    return  0;
}

输出聚类结果：

+ View Code

　

原文来自:博客园（华夏35度）http://www.cnblogs.com/zhangchaoyang 作者:Orisun

分类:  DM,NLP,AI

标签:  主成分分析,  Jama,  PCA,  Principal Component Analysis

本文出处：http://blog.csdn.net/xizhibei

=============================

PCA，也就是PrincipalComponents Analysis，主成份分析，是个很优秀的算法，按照书上的说法：

寻找最小均方意义下，最能代表原始数据的投影方法

然后自己的说法就是：主要用于特征的降维

另外，这个算法也有一个经典的应用：人脸识别。这里稍微扯一下，无非是把处理好的人脸图片的每一行凑一起作为特征向量，然后用PAC算法降维搞定之。

PCA的主要思想是寻找到数据的主轴方向，由主轴构成一个新的坐标系，这里的维数可以比原维数低，然后数据由原坐标系向新的坐标系投影，这个投影的过程就可以是降维的过程。

推导过程神马的就不扯了，推荐一个课件：http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf，讲得挺详细的

然后说下算法的步骤

1.计算所有样本的均值m和散布矩阵S，所谓散布矩阵同协方差矩阵；

2.计算S的特征值，然后由大到小排序；

3.选择前n'个特征值对应的特征矢量作成一个变换矩阵E=[e1, e2, …, en’]；

4.最后，对于之前每一个n维的特征矢量x可以转换为n’维的新特征矢量y：

  y = transpose(E)(x-m)

最后还得亲自做下才能记得住：用Python的numpy做的，用C做的话那就是没事找事，太费事了，因为对numpy不熟，下面可能有错误，望各位大大指正

 mat = np.load("data.npy")#每一行一个类别数字标记与一个特征向量
 data = np.matrix(mat[:,1:])
 avg = np.average(data,0)
 means = data - avg

 tmp = np.transpose(means) * means / N #N为特征数量
 D,V = np.linalg.eig(tmp)#DV分别对应特征值与特征向量组成的向量，需要注意下的是，结果是自动排好序的，再次膜拜numpy  OTL
 #print V
 #print D
 E = V[0:100,:]#这里只是简单取前100维数据，实际情况可以考虑取前80%之类的
 y = np.matrix(E) * np.transpose(means)#得到降维后的特征向量

 np.save("final",y)

另外，需要提一下的是OpenCV（无所不能的OpenCV啊OTL）中有PCA的实现：

 void cvCalcPCA( const CvArr* data,//输入数据
                 CvArr* avg, //平均（输出）
                 CvArr* eigenvalues, //特征值（输出）
                 CvArr* eigenvectors, //特征向量（输出）
                 int flags );//输入数据中的特征向量是怎么放的，比如CV_PCA_DATA_AS_ROW

最后，说下PCA的缺点：PCA将所有的样本（特征向量集合）作为一个整体对待，去寻找一个均方误差最小意义下的最优线性映射投影，而忽略了类别属性，而它所忽略的投影方向有可能刚好包含了重要的可分性信息

嗯，最后的最后——好了，没了，的确是最后了

强烈推荐：一篇能把PAC说得很透彻的文章《特征向量物理意义》：http://blog.sina.com.cn/s/blog_49a1f42e0100fvdu.html

版权声明：本文为博主原创文章，未经博主允许不得转载。

• 上一篇k-means--python版本
• 下一篇nbtscan局域网扫描的原理

顶