Trie树初探

Trie树

这个其实很简单,看下面这张图大家都能yy出来

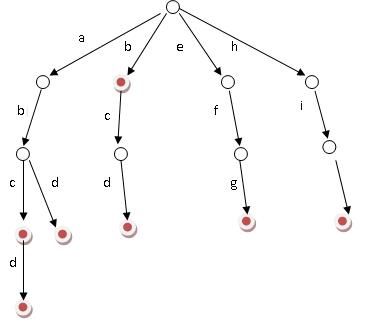
看完这个图我们看几道入门题

[HDOJ 1251] 统计难题

传送门

http://acm.hdu.edu.cn/showproblem.php?pid=1251

题目大意

给定一个字典,对于每个询问回答字典中含该前缀的单词数

题解

用这道题想明白所谓的动态开点即可(以下都由数组模拟指针来实现)
如果我们把所有点都开开,时间复杂度为 O(26lengthmax)
sum表示已开的节点数,每次从源点(定为0)开始向下寻找,如果没建立点就在sum+1的位置开一个点,我们要记录的只是这个点作为前缀所包含的单词数(每次经过+1)以及这个点它带的儿子的位置,由于本题的字符集为26,时间复杂度为 O(26∗sum+sum)

var
 x:array[0..1000000]of longint;
 y:array[0..1000000,1..26]of longint;
 i,j,k,tt,sum:longint;
 a,b:string;
function query(a:string):longint;
begin
 tt:=0;
 for i:=1 to length(a) do
  begin
   if y[tt,ord(a[i])-96]=0
   then exit(0)
   else tt:=y[tt,ord(a[i])-96];
  end;
 exit(x[tt]);
end;

procedure insert(a:string);
begin
 tt:=0;
 for i:=1 to length(a) do
  begin
   if y[tt,ord(a[i])-96]=0
   then begin inc(sum); y[tt,ord(a[i])-96]:=sum; end;
   inc(x[y[tt,ord(a[i])-96]]);
   tt:=y[tt,ord(a[i])-96];
  end;
end;

begin
 sum:=0; fillchar(x,sizeof(x),0);
 while not eof do
  begin
   readln(a);
   if a='' then break;
   insert(a);
  end;
 while not eof do
  begin
   readln(a);
   writeln(query(a));
  end;
end.

[HDOJ 1671] Phone List

传送门

http://acm.hdu.edu.cn/showproblem.php?pid=1671

题目大意

给定n个串,询问有没有哪个串是其他某个串的子串

[POJ 2001]Shortest Prefixes

传送门

http://poj.org/problem?id=2001

题目大意

求出最短唯一前缀

题解

在Trie树上打标记,每次一个单词经过一个节点,就+1,查询时遇到1它前面的节点就是答案

var
 Trie:array[0..100000]of longint;
 son:array[0..100000,0..26]of longint;
 x:array[0..10000]of string;
 i,j,k:longint;
 n,sum,tt:Longint;
procedure insert(a:string);
var i:longint;
begin
 tt:=0;
 for i:=1 to length(a) do
  begin
   if son[tt,ord(a[i])-96]=0
   then begin inc(sum); son[tt,ord(a[i])-96]:=sum; Trie[sum]:=1; end
   else inc(Trie[son[tt,ord(a[i])-96]]);
   tt:=son[tt,ord(a[i])-96];
  end;
end;

function query(a:string):string;
var b:string; i:longint;
begin
 b:=''; tt:=son[0,ord(a[1])-96];
 for i:=1 to length(a) do
  if Trie[tt]=1
  then exit(b+a[i])
  else begin b:=b+a[i]; if i<>length(a) then tt:=son[tt,ord(a[i+1])-96]; end;
 exit(b);
end;

begin
 n:=0; sum:=0;
 while not eof do
  begin
   inc(n); readln(x[n]); //if x[n]='' then begin dec(n); break; end;
   insert(x[n]);
  end;
 for i:=1 to n do
  writeln(x[i],' ',query(x[i]));
end.

POJ 3764

传送门

http://poj.org/problem?id=3764

题目大意

给定一棵树,找一条简单路径,使其边权抑或值最大

题解

xor是Trie树的经典应用
首先(a  xor  b)xor(a  xor  c)=b  xor  c也就是说定义两点间边权抑或f(u,v)=f(1,u)  xor  f(1,v)，O(N)实现
然后原问题就转化为,两点抑或值最大 O(N2) 实现会超时
所以我们把每个值转成二进制倒着插入 Trie 中,也就是说3我们插入的是00000000000000000000000000011,然后枚举每个权值,再在Trie中找与它抑或值最大的
找的时候贪心即可,即找x[i]时,每次x[i]的该位二进制为1能走0就走不能就走1

理论AC,,,,,UOJ自定义测试都能跑起来,交上去就是运行错误,,,,,

const
  maxn=100005;
var
  w:array[0..4*maxn,1..3]of longint;
  s:array[0..5*maxn,1..2]of longint;
  x,y:array[0..maxn]of longint;
  i,j,k:longint;
  n,a,b,c,len,sum,ans:longint;
function max(a,b:longint):Longint;
begin
  if a>b then exit(a) else exit(b);
end;

procedure init(a,b,c:longint);
begin
  w[len,1]:=b; w[len,2]:=c;
  if w[a,3]=0
  then w[a,3]:=len else w[w[a,1],3]:=len;
  w[a,1]:=len; inc(len);
end;

procedure dfs(a:longint);
var tt:longint;
begin
  y[a]:=1; tt:=w[a,3];
  while tt<>0 do
    begin
      if y[w[tt,1]]=0
      then begin x[w[tt,1]]:=x[a] xor w[tt,2]; dfs(w[tt,1]); end;
      tt:=w[tt,3];
    end;
end;

procedure init(a:longint);
var i,tt,b:longint;
begin
  tt:=0;
  for i:=31 downto 1 do
    begin
      if (a and (1<<(i-1)))=0
      then b:=0 else b:=1;
      if s[tt,b]=0
      then begin inc(sum); s[tt,b]:=sum; end;
      tt:=s[tt,b];
    end;
end;

function check(a:longint):longint;
var tt1,tt2,i,b,c,anss:longint;
begin
  tt1:=0; tt2:=0; anss:=0;
  for i:=31 downto 1 do
    begin
      if a and(1<<(i-1))=0 then b:=0 else b:=1;
      c:=b xor 1;
      if s[tt2,c]=0
      then tt2:=s[tt2,b]
      else begin tt2:=s[tt2,c]; inc(anss,1<<(i-1)); end;
      tt1:=s[tt1,b];
    end;
  exit(anss);
end;

begin
  readln(n); len:=n+1;
  for i:=1 to n-1 do
    begin
      readln(a,b,c);
      inc(a); inc(b);
      init(a,b,c); init(b,a,c);
    end;
  x[1]:=0;
  dfs(1);
  sum:=0;
  fillchar(s,sizeof(s),0);
  for i:=1 to n do
    init(x[i]);
  ans:=0;
  for i:=1 to n do
    ans:=max(ans,check(x[i]));
  writeln(ans);
end.