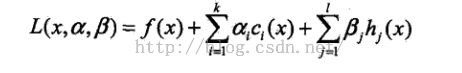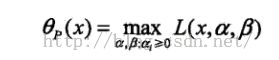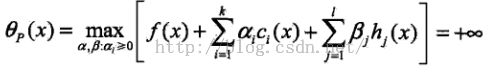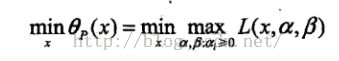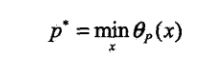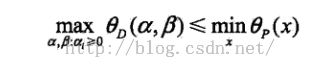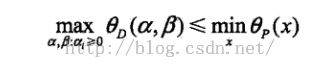拉格朗日对偶性
1.原始问题
假设f(x),ci(x),hj(x)是定义在
上的连续可微函数，考虑约束最优化问题
称此越是最优化问题为原始最优化问题或原始问题。
首先，引入广义拉格朗日函数（generalized Lagrange function）
这里，
是拉格朗日乘子，αi>=0，考虑x的函数：
这里，P表示是原始问题。
假设给定某个x，如果x违反原始问题的约束条件，即存在某个i使得ci(w)>0，或者存在某个j使得hj(w)≠0，那久有
因为若某个i使约束ci(x)>0，则可令αi->∞，若某个j使hj(x)≠0，则可令βj使βjhj(x)->∞，而将其与各αi，βj均取0.
相反，如果x满足（C.2）和（C.3）,则可知，。因此，
所以如果考虑极小化问题
它与原始问题（C.1）~（C.3）是等价的，即他们有相同的解。问题
成为广义拉格朗日函数的极小极大问题。这样一来，就把原始最优化问题表示为广义拉格朗日函数的极小极大问题。
为了方便，定义原始问题的最优值
（看晕了的同学，你要知道它求的一直都是f(x)，通过给L加了约束条件，去优化L实际上就是优化f(x))
2.对偶问题
定义
在考虑极大化，即
该问题称为广义拉格朗日函数的极大极小问题。可以将广义拉格朗日函数的极大极小问题表示为越是最优化问题：
称为原始问题的对偶问题，定义对偶问题的最优值
3.原始问题和对偶问题的关系
定理：若原始问题和对偶问题都有最优值，则
证明 ：
对任意的α，β和x，有
即
由于原始问题和对偶问题均有最优值，所以，
即
推论 设x*和α*，β*分别是原始问题和对偶问题的可行解，则x*和α*，β*分别是原始问题和对偶问题的最优解。
在某些条件下，原始问题和对偶问题的最优值相等d*=p*。这时可以用对偶问题替代原始问题。
下面以定理的形式叙述有关的重要结论而不予证明。
定理2 考虑原始问题和对偶问题，假设函数f(x)和ci(c)是凸函数,hj(x)是仿射函数；并且假设不等式约束ci(x)是严格可行的，即存在x，对所有i有ci(x)<0,则存在x*,α*，β*，是x*是原始问题的解，α*，β*是对偶问题的解，并且
定理3 对原始问题和对偶问题，假设函数f(x)和ci(c)是凸函数,hj(x)是仿射函数并且假设不等式约束ci(x)是严格可行的，即存在x，对所有i有ci(x)<0,则存在x*,α*，β*，是x*是原始问题的解，α*，β*是对偶问题的解的充分必要条件是x*，α*，β*满足下面Karush-Kuhn_Tucker（KKT）条件：
其中
称为KKT的对偶互补条件，由此条件可知，若α*>0,则ci(x*)>0；