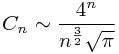【算法】Catalan数

1.介绍

1.1 什么是Catalan数

Catalan序列是一个整数序列，其通项公式：；取第n项即为第n个Catalan数，前几个Catalan数：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, … 

1.2  一些性质

1、

这是根据原来的式子推导出来的，大概过程是这样的：

2、

这个递推式很容易可以从原来的式子中获得

3、

4、

5、

这个是Catalan数的增长趋势。

（以上内容均摘自[1]，关于Catalan数介绍得详细易懂）

2. Referrence

[1] daybreakcx，小思Catalan数     

[2] 五岳，从《编程之美》买票找零问题说起，娓娓道来卡特兰数——兼爬坑指南

[3] wuzhekai1985，解题笔记（37）——Catalan数计算及应用

3. 应用

3.1 二叉树构造问题

描述：n个节点可以构造多少种不同的二叉树。

假设n个节点的二叉树有h(n)种，将一个节点做根节点，二叉树被分为三个部分：根节点、及根节点的左右子树。设左子树节点数为i，且i=0, 1, ... , n-1；则右子树的节点数为n-i-1。左右子树的不同种数分别为h(i)、h(n-i-1)，对左右子树节点数分别为i、n-i-1的二叉树，其不同种数是h(i)*h(n-i-1)；得递推公式：

h(n)=h(0)*h(n-1)+h(1)*h(n-2)+ ... +h(n-1)*h(0)

h(0)=h(1)=1

易知h(n)即为Catalan数。

3.1.1 POJ 1095

二叉树按一定规则进行构造：（1）节点数少的二叉树的编号小于节点数多的二叉树；（2）相同节点数的二叉树，先比较左子树，左子树的编号大的二叉树编号大；若左子树编号相同，则比较右子树编号；即构造二叉树先从右至左开始构造。对给定的编号，输出二叉树。

这里详细地给出了解题思路，但有一些地方没说清楚。

__int64 输入应该用"%I64d"。切记切记！

源代码：

1095

Accepted

172K

0MS

C

888B

2013-09-23 16:20:54

#include <stdio.h>

#define MAX 19

__int64 catalan[MAX],sum[MAX];

/*compute catalan number and its sum*/
void compute()
{
	int i;
	catalan[0]=catalan[1]=1;
	sum[1]=1;
	for(i=2;i<MAX;i++)
	{
		catalan[i]=(4*i-2)*catalan[i-1]/(i+1);
		sum[i]=sum[i-1]+catalan[i];
	}
}

void solve(__int64 n,__int64 k)
{
	int i;	
	if(n==1)
	{
		printf("X");
		return;
	}

	for(i=0;i<n;i++)
	{
		if(k<=catalan[i]*catalan[n-1-i])
			break;
		else
			k-=catalan[i]*catalan[n-1-i];
	}

    /*print left subtree*/
	if(i>0)
	{
		printf("(");
		solve(i,(k-1)/catalan[n-i-1]+1);
		printf(")");
	}
	printf("X");

    /*print right subtree*/
	if(n-i-1>0)
	{
		printf("(");
		solve(n-i-1,(k-1)%catalan[n-i-1]+1);
		printf(")");
	}
}

int main()
{
	int n;
	__int64 order;
	compute();
	while(scanf("%I64d",&order)&&order)
	{
		for(n=1;n<MAX;n++)
		{
			if(order<=sum[n])
				break;
		}
		solve(n,order-sum[n-1]);
		printf("\n");
	}
	return 0;
}

3.2 圆上点互连问题

描述：将圆上有2n个点成对连接起来，并且所得的n条线段不相交，求可行方法数[2]。

设2n个点时方法数为h(n)。选择一个点标记为1，然后顺时针一次标记点2, 3, ... , 2n；则与点1相连的点必为偶数。因为，若与点1相连的点为奇数x，则位于点1与点x之间的点数为x-2（奇数），意味着这x-2个点中必剩下一个点与比点x大的点相连，即会出现线段相交。所以与点1相连的点必为偶数。

假设点1与点2i（i=1, 2, ... , n-1）相连，则2n个点分为了三个部分：（1）点1与点2i；（2）点2、点3....点2i-2；（3）点2i+1...点2n。第（2）部分可行方法数为h(i-1)，第（3）部分可行方法数为h(n-i)。还有一种特殊情况，点1与点2n相连，可行方法数为h(n-1)。易得递推公式：

h(n)=h(0)*h(n-1)+h(1)*h(n-2)+ ... +h(n-1)

h(0)=h(1)=1

h(n)即为 Catalan数。

3.2.1 POJ 2084

求高精度Catalan数。

懒得写高精度，在网上找了一份代码，当然写得比我好多了。

源代码：

2084

Accepted

208K

0MS

C

849B

2013-09-23 20:22:46

#include "stdio.h"
#include "string.h"

#define MAXN 101
#define MAX 100
#define BASE 10000

void Multiply(int a[],int len,int b)
{
	int i,carry;
	for(i=len-1,carry=0;i>=0;i--)
	{
		carry+=b*a[i];
		a[i]=carry%BASE;
		carry/=BASE;
	}
}

void Divide(int a[],int len,int b)
{
	int i,div;
	for(i=0,div=0;i<len;i++)
	{
		div=div*BASE+a[i];
		a[i]=div/b;
		div%=b;
	}
}

int main()
{
	int i,j,catalan[MAXN][MAX];
	memset(catalan[1],0,MAX*sizeof(int));
	
	for(i=2,catalan[1][MAX-1]=1;i<MAXN;i++)
	{
		memcpy(catalan[i],catalan[i-1],MAX*sizeof(int));
		Multiply(catalan[i],MAX,4*i-2);
		Divide(catalan[i],MAX,i+1);
	}
	
	while(scanf("%d",&i) && i!=-1)
	{
		for(j=0;j<MAX && catalan[i][j]==0;j++);
		for(printf("%d",catalan[i][j++]);j<MAX;j++)
			printf("%04d",catalan[i][j]);
		printf("\n");
	}
	return 0;
}

3.3 入栈出栈问题

描述：n个元素入栈后出栈，求出栈序列有多少种。

元素的出栈情况比较复杂：可以一入栈就出栈，也可以入栈后等若干个元素入栈后再依次出栈。比如，有三个元素1、2、3，并按1 2 3的顺序入栈，其出栈序列：（1）1 2 3入栈后开始出栈，则出栈序列为3 2 1。（2）1 2入栈后开始出栈，2出栈后3入栈，此时栈中元素是3 1，出栈序列为2 3 1；也有可能2 1出栈后3入栈，则出栈序列为2 1 3。（3）……

注意，元素1是第一个入栈的，如果元素1是第i个出栈，说明在元素1之前已有i-1个元素入栈并出栈，还剩下n-i个元素没入栈也没出栈。先考虑3个元素的出栈序列，

（1）当元素1是第一个出栈时，意味着在元素1之前没有元素入栈并出栈，还剩下两个元素2 3没有入栈和出栈；元素2 3的出栈序列有两种：2 3和3 2；所以，3个元素的出栈序列有两种：1 2 3和1 3 2。

（2）当元素1是第二个出栈时，意味着在元素1之前已有1个元素入栈并出栈，这个元素只有可能是2，还剩下1个元素3没有入栈和出栈；出栈序列只有一种：2 1 3。

（3）当元素1是第三个出栈时，意味着在元素1之前已有2个元素入栈并出栈，这两个元素是2 3，出栈序列有两种：2 3和3 2；所以，3个元素的出栈序列有两种：2 3 1和3 2 1。

用归纳法求所有出栈序列。假设n个元素（1 2 ... n）的出栈序列有h(n)种。

（1）当元素1第一个出栈时，说明在元素1之前没有元素入栈并出栈，剩下n-1个元素（2 ...n-1 n）没有入栈和出栈；n-1个元素的出栈序列有h(n-1)种；所以，n个元素的出栈序列有h(n-1)种。

……

（ i ）当元素1第i个出栈时，说明在元素1之前已有i-1个元素入栈并出栈，还剩下n-i个元素没入栈也没出栈；所以，出栈序列有h(i-1)*h(n-i)。

……

易得递推公式：h(n)=h(n-1)+h(1)*h(n-2)+ ... +h(n-1)*h(0)，即得证。

将入栈设为状态1，出栈设为状态0；n个元素的入栈和出栈，对应地会有n个1和n个0，组成了2n位的2进制数。这个问题还可以进一步转化：从左到右扫描，1的累计数不小于0的累计数，求满足这样条件的2n位2进制数有多少。把入栈看作左括号，出栈看作右括号，则n个元素的入栈出栈问题变成了n对括号的匹配问题。