机器学习之K近邻算法

K近邻算法(K Nearest Neighbor, KNN)可以说是最简单的算法，但是其基本的思想却在许多算法中出现，比如：个性化推荐系统中，基于用户(based users)或者是基于商品(based items)算法，都是先根据相似度进行排序，然后选取前k个作为推荐的对象，当然这与KNN算法还是有一些出入，但是其基本思想我认为是一致的。有的人说KNN是用于分类算法的，但是我觉得把KNN算法作为回归似乎也是可以的，比如我们取K个近邻的均值作为预测结果，或者直接依据K个近邻使用最小二乘法(后面有机会，会专门写一篇博客介绍最小二乘法)，不过这篇文章还是根据Machine Learning Action进行讲解，并且进行相应的补充，主要是在相似度计算这一块，加强一些。下面是KNN算法的步骤：
遍历数据集并且计算和带预测样本的相似度，选取前k个最相似的实例，这k个样本中最大的类别数目作为最终预测样本的类别。
说句实话，KNN本身并没有什么太多的研究价值，下面我打算借此机会介绍一下常用的相似度计算：
1 欧几里得距离(Euclidean Distance, ED):

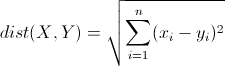
2 曼哈顿距离(Manhattan Distance， MD):

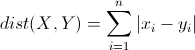
3 余弦相似度(Cosine Similarity)

4 Jaccard相似系数

5 皮尔森相关系数(Pearson Correlation Coefficient

下面是Python的代码。

from numpy import *
import operator
from os import listdir
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]  # row_size
    diffMat = tile(inX, (dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    print sqDiffMat
    sqDistances = sqDiffMat.sum(axis=1) # axis = 0 for col, and axis = 1 for row
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort()
    classCount={}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.iteritems(), key=lambda x:x[1], reverse=True)
    return sortedClassCount[0][0]
def file2maxtrix(filename):
    fr = open(filename)
    numberOfLines = len(fr.readlines())
    returnMat = zeros((numberOfLines,3))
    classLabelVector = []
    fr = open(filename)
    index = 0
    for line in fr.readlines():
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:]=listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1]))
        index += 1
    return returnMat,classLabelVector
def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = shape(dataSet)[0]
# print dataSet.shape(0)
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges,(m,1))
    return normDataSet, ranges, minVals
def datingClassText():
    hoRatio = 0.10
    datingDataMat, datingLabels = file2maxtrix('datingTestSet2.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    m = shape(normMat)[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print "the total error rate is: %f" % (errorCount/float(numTestVecs))
def classifyPerson():
    resultList = ['not at all','in small doses', 'in large doses']
    percentTats = float(raw_input("percentage of time spent playing video games?"))
    ffMiles = float(raw_input("frequent flier miles earned per year?"))
    iceCream = float(raw_input("liters of ice cream consumed per year?"))
    datingDataMat,datingLabels = file2maxtrix('datingTestSet2.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    inArr = array([ffMiles, percentTats, iceCream])
    classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels,3)
    print "You will probably like this person: ",resultList[classifierResult - 1]
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect
def handwritingClassTest():
    hwLabels = []
    trainingFileList = listdir('digits/trainingDigits')
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('digits/trainingDigits/%s' % fileNameStr)
    testFileList = listdir('digits/testDigits')        #iterate through the test set
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('digits/testDigits/%s' % fileNameStr)
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
        if (classifierResult != classNumStr): errorCount += 1.0
    print "\nthe total number of errors is: %d" % errorCount
    print "\nthe total error rate is: %f" % (errorCount/float(mTest))
    datingDataMat, datingLabels = file2maxtrix('datingTestSet2.txt')
# fig = plt.figure()
# ax = fig.add_subplot(111)
# ax.scatter(datingDataMat[:,1], datingDataMat[:,2],15.0*array(datingLabels),15.0*array(datingLabels))
# ax.axis([-2,25,-0.2,2.0])
# plt.xlabel('Percentage of Time Spent Playing Video Games')
# plt.ylabel('Liters of Ice Cream Consumed Per Week')
# plt.show()
# normMat, ranges, minVals = autoNorm(datingDataMat)
# print normMat
# print ranges
# print minVals
# datingClassText()
# classifyPerson()
# testVector =img2vector('digits/testDigits/0_13.txt')
# print testVector[0,0:31]
# # print testVector[0,32:63]
# handwritingClassTest()
import numpy as np
import matplotlib.pyplot as plt

x = np.random.rand(3, 2) * 10
a = np.matrix([ [1,x[0][0]], [1,x[1][0]], [1,x[2][0]] ])
b = np.matrix([ [x[0][1]], [x[1][1]], [x[2][1]] ])
yy = (a.T * a).I * a.T * b
xx = np.linspace(1, 10, 50)
y = np.array(yy[0] + yy[1] * xx)

plt.figure(1)
plt.plot(xx, y.T, color='r')
plt.scatter([x[0][0], x[1][0], x[2][0] ], [x[0][1], x[1][1], x[2][1] ])
plt.show()