Codeforces 519E - A and B and Lecture Rooms (LCA)

题意：给一棵树，M次询问，每次询问到两个点距离相等的点的个数。

519E - A and B and Lecture Rooms

Author: Bekzhan.Kassenov

In this problem we have to answer to the following queries on tree: for given pairs of vertices your program should output number of eqidistand vertices from them.

Let's denote:

dist(a, b) as distance between vertices a and b.

LCA(a, b) as lowest common ancestor of vertices a and b.

depth[a] as distance between root of the tree and vertex a.

size[a] as size of subtree of vertex a.

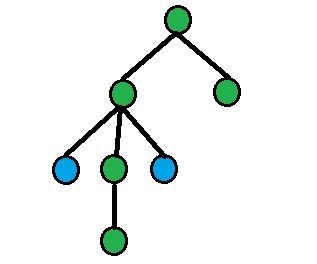
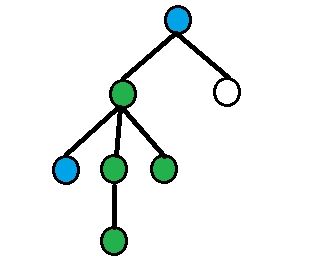
On each picture green nodes are equidistant nodes, blue nodes — nodes from query.

Preprocessing: Read edges of tree and build data structure for LCA (it is more convenient to use binary raise, becase we will use it further for other purposes).

Complexity: O(NlogN)

Queries:

We have to consider several cases for each query:

1) a = b. In that case answer is n.

2) dist(a, b) is odd. Then answer is 0.

3) dist(a, l) = dist(b, l), where l = LCA(a, b).

Find children of l, which are ancestors of a and b (let's denote them as aa and bb). Answer will ben - size[aa] - size[bb].

4) All other cases.

 

Assume that depth[a] > depth[b]. Then using binary raise find dist(a, b) / 2-th ancestor of a (let's denote it as p1),dist(a, b) / 2 - 1-th ancestor of vertex a (denote it as p2). Answer will be size[p1] - size[p2].

Complexity: O(logN) for each query, O(MlogN) for all queries.

Resulting complexity:: O(MlogN + NlogN)

Code: 10083310

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define prt(k) cout<<#k" = "<<k<<endl;
typedef long long ll;
const int N = 100005;
int n, m, head[N], mm;
struct Edge {
    int to, next;
}e[N << 1];
void add(int u, int v)
{
    e[mm].to = v;
    e[mm].next = head[u];
    head[u] = mm++;
}
int sz[N], dep[N];
int f[N][22];
void dfs(int u, int fa)
{
    dep[u] = dep[fa] + 1;
    f[u][0] = fa;
    sz[u] = 1;
    for (int i=head[u];~i;i=e[i].next)
    {
        int v = e[i].to;
        if (v != fa)
        {
            dfs(v, u);
            sz[u] += sz[v];
        }
    }
}
int maxh;
void gao()
{
    int j;
    for (j=1;(1<<j)<n;j++)
        for (int i=1;i<=n;i++)
        f[i][j] = f[f[i][j-1]][j-1];
    maxh = j - 1;
}
int swim(int x, int k)
{
    for (int i=0;i<=maxh;i++)
        if (k >> i & 1)
        x = f[x][i];
    return x;
}
int LCA(int x, int y)
{
    if (dep[x] > dep[y]) swap(x, y); ///dep[x] <= dep[y];
    y = swim(y, dep[y] - dep[x]);
    if (x == y) return y;
    for (int i=maxh; i>=0; i--) {
        if (f[x][i] != f[y][i])
            x = f[x][i], y = f[y][i];
    }
    return f[x][0];
}
int main()
{
    dep[0] = 1;
    cin >> n ;
    mm = 0;
    memset(head, -1, sizeof head);
    for (int i=1;i<n;i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        add(u, v);  add(v, u);
    }
    dfs(1, 0);
    gao();
   /** prt(maxh);
    for (int i=1;i<=n;i++)
    {
        for(int j=0;j<=maxh;j++)
        {
            printf("f[%d][%d] = %d\n", i,j,f[i][j]);
        }
    }
    for (int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            printf("LCA(%d, %d) = %d\n", i,j,LCA(i,j)); */
    cin >> m;
    for (int i=0;i<m;i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        if (x == y) {
            printf("%d\n", n);
            continue;
        }
        if (dep[x] < dep[y])
            swap(x, y);
        int z = LCA(x, y);
        int dist = dep[x] + dep[y] - dep[z] - dep[z];
        if (dist & 1) {
            printf("0\n");
            continue;
        }
        dist /= 2;
        int da = dep[x] - dep[z];
        int db = dep[y] - dep[z];
        if (da == db) {
            int aa = swim(x, da-1);
            int bb = swim(y, db - 1);
            int ans = n - sz[aa] - sz[bb];
            printf("%d\n", ans);
            continue;
        }
        int p1 = swim(x, dist);
        int p2 = swim(x, dist-1);
        int ans = sz[p1] - sz[p2];
        printf("%d\n", ans);
    }
}