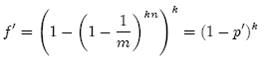Bloom filter 过滤(布隆过滤算法)原理
一,什么是Bloom filter
Bloom filter 是由 Howard Bloom 在 1970 年提出的二进制向量数据结构,它具有很好的空间和时间效率,被用来检测一个元素是不是集合中的一个成员,这种检测只会对在集合内的数据错判,而不会对不是集合内的数据进行错判,这样每个检测请求返回有“在集合内(可能错误)”和“不在集合内(绝对不在集合内)”两种情况,可见 Bloom filter 是牺牲了正确率换取时间和空间。
二,bloom filter的计算方法
如需要判断一个元素是不是在一个集合中,我们通常做法是把所有元素保存下来,然后通过比较知道它是不是在集合内,链表、树都是基于这种思路,当集合内元素个数的变大,我们需要的空间和时间都线性变大,检索速度也越来越慢。 Bloom filter 采用的是哈希函数的方法,将一个元素映射到一个 m 长度的阵列上的一个点,当这个点是 1 时,那么这个元素在集合内,反之则不在集合内。这个方法的缺点就是当检测的元素量很多时候可能有冲突,解决方法就是使用 k 个哈希 函数对应 k 个点,如果所有点都是 1 的话,那么元素在集合内,如果有 0 的话,元素则不再集合内。
三,bloom filter的特点
Bloom filter 优点就是它的插入和查询时间都是常数,另外它查询元素却不保存元素本身,具有良好的安全性。它的缺点也是显而易见的,当插入的元素越多,错判“在集合内”的概率就越大了,另外 Bloom filter 也不能删除一个元素,因为多个元素哈希的结果可能在 Bloom filter 结构中占用的是同一个位,如果删除了一个比特位,可能会影响多个元素的检测。
集合表示和元素查询
下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0。
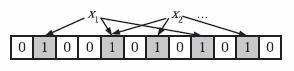
为了表达S={x1, x2,…,xn}这样一个n个元素的集合,Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x,第i个哈希函数映射的位置hi(x)就会被置为1(1≤i≤k)。注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位)。
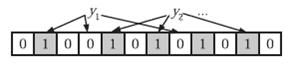
在判断y是否属于这个集合时,我们对y应用k次哈希函数,如果所有hi(y)的位置都是1(1≤i≤k),那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中y1就不是集合中的元素。y2或者属于这个集合,或者刚好是一个false positive。
错误率估计
前面我们已经提到了,Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率(false positive rate),下面我们就来估计错误率的大小。在估计之前为了简化模型,我们假设kn<m且各个哈希函数是完全随机的。当集合S={x1, x2,…,xn}的所有元素都被k个哈希函数映射到m位的位数组中时,这个位数组中某一位还是0的概率是:
其中1/m表示任意一个哈希函数选中这一位的概率(前提是哈希函数是完全随机的),(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中,需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它,因此这个概率就是(1-1/m)的kn次方。令p = e-kn/m是为了简化运算,这里用到了计算e时常用的近似:
令ρ为位数组中0的比例,则ρ的数学期望E(ρ)= p’。在ρ已知的情况下,要求的错误率(false positive rate)为:
(1-ρ)为位数组中1的比例,(1-ρ)k就表示k次哈希都刚好选中1的区域,即false positive rate。上式中第二步近似在前面已经提到了,现在来看第一步近似。p’只是ρ的数学期望,在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明[2] ,位数组中0的比例非常集中地分布在它的数学期望值的附近。因此,第一步的近似得以成立。分别将p和p’代入上式中,得:
相比p’和f’,使用p和f通常在分析中更为方便。
最优的哈希函数个数
既然Bloom Filter要靠多个哈希函数将集合映射到位数组中,那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢?这里有两个互斥的理由:如果哈希函数的个数多,那么在对一个不属于集合的元素进行查询时得到0的概率就大;但另一方面,如果哈希函数的个数少,那么位数组中的0就多。为了得到最优的哈希函数个数,我们需要根据上一小节中的错误率公式进行计算。
先用p和f进行计算。注意到f = exp(k ln(1 ? e?kn/m)),我们令g = k ln(1 ? e?kn/m),只要让g取到最小,f自然也取到最小。由于p = e-kn/m,我们可以将g写成
根据对称性法则可以很容易看出当p = 1/2,也就是k = ln2· (m/n)时,g取得最小值。在这种情况下,最小错误率f等于(1/2)k ≈ (0.6185)m/n。另外,注意到p是位数组中某一位仍是0的概率,所以p = 1/2对应着位数组中0和1各一半。换句话说,要想保持错误率低,最好让位数组有一半还空着。
需要强调的一点是,p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 ? (1 ? 1/m)kn)),g’ = k ln(1 ? (1 ? 1/m)kn),p’ = (1 ? 1/m)kn,我们可以将g’写成
同样根据对称性法则可以得到当p’ = 1/2时,g’取得最小值。
位数组的大小
下面我们来看看,在不超过一定错误率的情况下,Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素,允许的最大错误率为?,下面我们来求位数组的位数m。
假设X为全集中任取n个元素的集合,F(X)是表示X的位数组。那么对于集合X中任意一个元素x,在s = F(X)中查询x都能得到肯定的结果,即s能够接受x。显然,由于Bloom Filter引入了错误,s能够接受的不仅仅是X中的元素,它还能够? (u - n)个false positive。因此,对于一个确定的位数组来说,它能够接受总共n + ? (u - n)个元素。在n + ? (u - n)个元素中,s真正表示的只有其中n个,所以一个确定的位数组可以表示
个集合。m位的位数组共有2m个不同的组合,进而可以推出,m位的位数组可以表示
个集合。全集中n个元素的集合总共有
个,因此要让m位的位数组能够表示所有n个元素的集合,必须有
即:
上式中的近似前提是n和?u相比很小,这也是实际情况中常常发生的。根据上式,我们得出结论:在错误率不大于?的情况下,m至少要等于n log2(1/?)才能表示任意n个元素的集合。
上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小,这时f = (1/2)k = (1/2)mln2 / n。现在令f≤?,可以推出
这个结果比前面我们算得的下界n log2(1/?)大了log2 e ≈ 1.44倍。这说明在哈希函数的个数取到最优时,要让错误率不超过?,m至少需要取到最小值的1.44倍。
总结
在计算机科学中,我们常常会碰到时间换空间或者空间换时间的情况,即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素:错误率。在使用Bloom Filter判断一个元素是否属于某个集合时,会有一定的错误率。也就是说,有可能把不属于这个集合的元素误认为属于这个集合(False Positive),但不会把属于这个集合的元素误认为不属于这个集合(False Negative)。在增加了错误率这个因素之后,Bloom Filter通过允许少量的错误来节省大量的存储空间。
出处:http://blog.163.com/kevinlee_2010/blog/static/1698208202011112810411190/