立方体的纹理映射(黑白色交替)
1. 使用透视投影,即有(phi,theta,R),
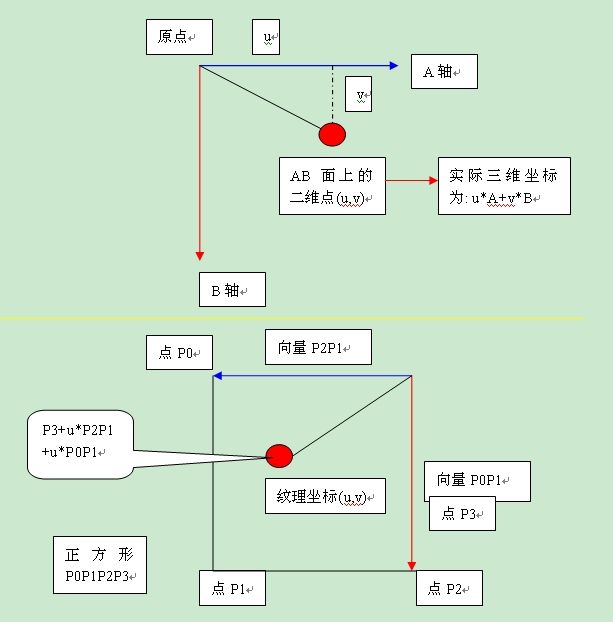
2.在一个平面(P0,P1,P2,P3)(该平面为空间任一平面,可能是斜的)上,以某点为XY坐标系的原心(如P3),获取纹理坐标(u,v)上的点的实际坐标Pm,再将其投影(Project())到二维显示器上,并设置点颜色(SetPixel())为黑色或白色.其中计算(u,v)上的点的实际坐标Pm方法如下(其中P0P1P2P3是正方形,P3=P2-P1+P0,Pm= P3+u*P2P1+u*P0P1=(P1-P0)*u+(P1-P2)*v+P2-P1+P0):
3.结果显示的是一个8*8的黑色国际象棋立方体,可由int(u*8.0)+int(v*8.0))能否被2整除来决定,可代入数据(u,v)分析出来,如想结果为int(1+1),或int(1+2)等.
4.不过,<计算机图形学VC++ 孔令德>里的代码只适合离散点,即只是离散地绘制像素,并没有画一个面.当u,v的步长很大时,会看到明显的间断.源代码如下:
5.
for(double u=0.0;u<=1.0;u+=0.005)
for(double v=0.0;v<=1.0;v+=0.005)
{
if((int(u*8.0)+int(v*8.0))%2==0)//黑白交替
{
a=0.1;
Pm.x=(Pk[1].x-Pk[0].x)*u+(Pk[1].x-Pk[2].x)*v+Pk[2].x-Pk[1].x+Pk[0].x;
Pm.y=(Pk[1].y-Pk[0].y)*u+(Pk[1].y-Pk[2].y)*v+Pk[2].y+Pk[0].y-Pk[1].y;
Pm.z=(Pk[1].z-Pk[0].z)*u+(Pk[1].z-Pk[2].z)*v+Pk[2].z+Pk[0].z-Pk[1].z;
Pn=Project(Pm);
pDC->SetPixel(MaxX/2+ROUND(Pn.x),MaxY/2-ROUND(Pn.y),RGB(a*255,a*255,a*255));
}
else
{
b=0.9;
Pm.x=(Pk[1].x-Pk[0].x)*u+(Pk[1].x-Pk[2].x)*v+Pk[2].x-Pk[1].x+Pk[0].x;
Pm.y=(Pk[1].y-Pk[0].y)*u+(Pk[1].y-Pk[2].y)*v+Pk[2].y+Pk[0].y-Pk[1].y;
Pm.z=(Pk[1].z-Pk[0].z)*u+(Pk[1].z-Pk[2].z)*v+Pk[2].z+Pk[0].z-Pk[1].z;
Pn=Project(Pm);
pDC->SetPixel(MaxX/2+ROUND(Pn.x),MaxY/2-ROUND(Pn.y),RGB(b*255,b*255,b*255));
}
}